Лекция 7

;;

При

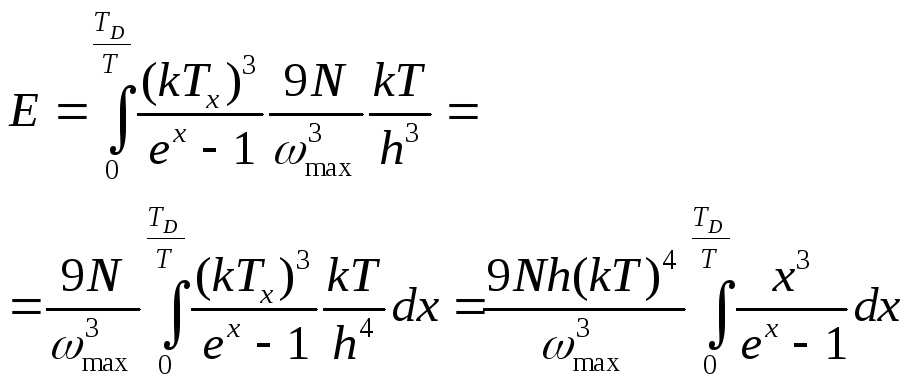
1)

;

для 1 моля.

- молярная теплоёмкость.

2)

;

.

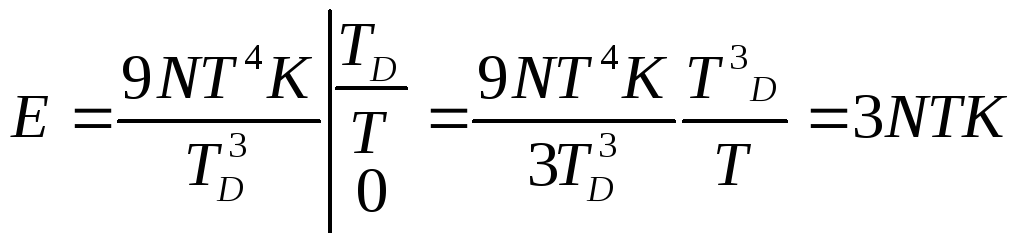- Закон Дюлонга и Пти.

- температура Дебая.

Вычисление электрохимического потенциала для классической системы.

Число макросостояний, с помощью которого может быть реализовано данное микросостояние называется термодинамической вероятностью, характеризуется функцией распределения по энергиям.

Вид функции определяется по теории вероятностей.

- функция вероятности для классической системы.

Где - электрохимический потенциал.

- вероятность их нахождения

(число частиц)

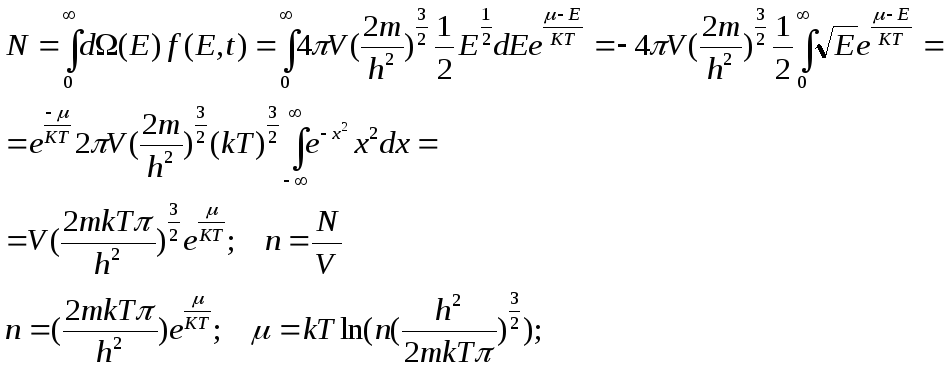
(концентрация)

- функция вероятности для классической системы.

Система, которая подчиняется квантовой статистике, называется вырожденной. Система, которая отвечает классической статистике, называется невырожденной. Электронный газ в металле будет представлять вырожденную систему, подчиняющуюся статистике Ферми-Дерака.

Электронный газ в металле при абсолютном нуле.

Для расчёта электронного газа в металле при абсолютном нуле сделаем следующее предположения:

1. Все атомы металла 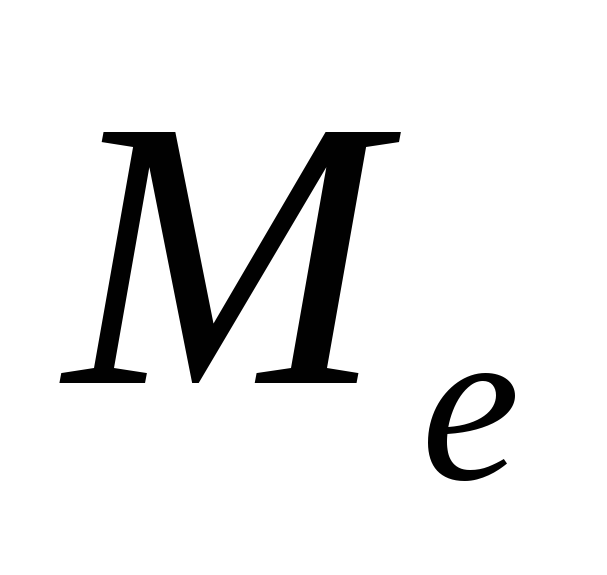, т.е. число атомов равно числу свободных электронов.

2. положительный заряд ионов как бы размазан по объёму кристалла.

Электронный газ в металле подчиняется функции распределения Ферми-Дерака.

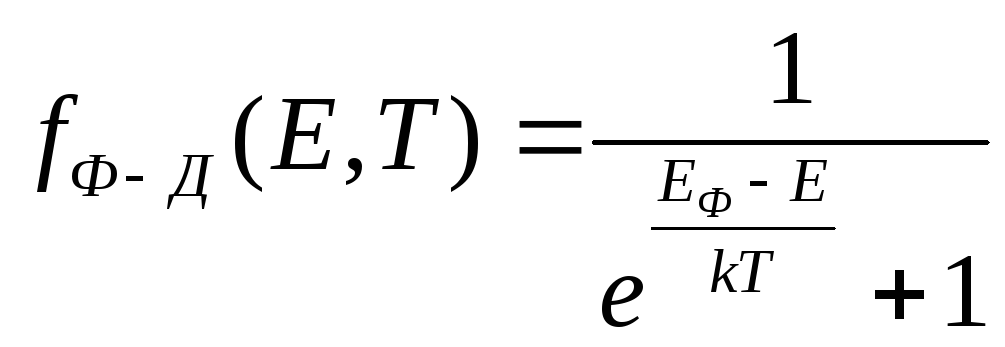
При

1)

2)

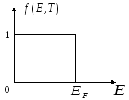
При Т=0 электроны в электронном газе обладают наименьшей энергией и будет распределён по энергетическим уровням в соответствии принципам запрета Паули. Энергия Ферми для электронного газа в металле – энергия, соответствующая наивысшему заполненному энергетическому уровню при Т=0. Энергию Ферми для электронного газа в металле можно найти из условия нормировки.

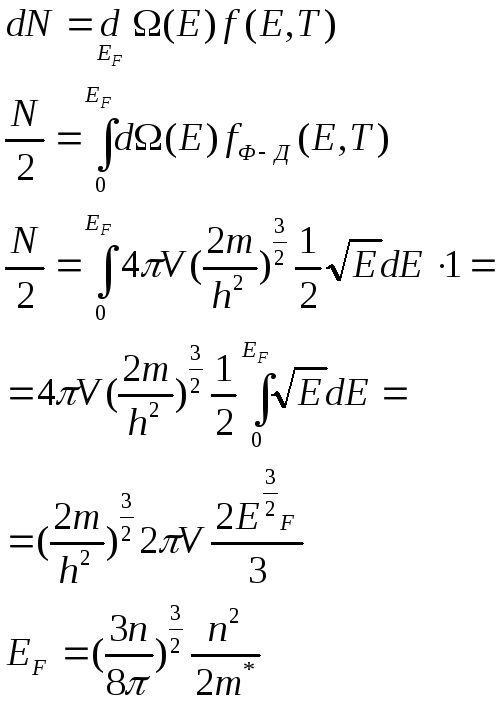
- эффективная масса.

Для всех

Вычисление средней энергии электронов в .

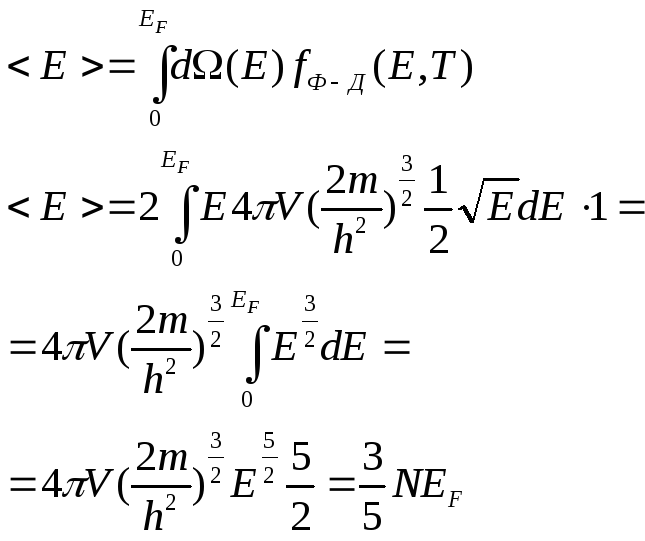
N– количествосвойств.

Электронный газ в металле при Т не равном 0.

При энергией Ферми считаем такую энергию, которая соответствует энергетическому уровню, вероятность заполнения которого равна ½.

При повышении температуры в электронном газе происходит перераспределение электронов по энергетическим уровням. При повышении температуры энергия Ферми уменьшается.

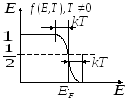
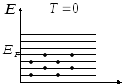
Эффективная масса.

Эффективная масса не имеет такого физического смысла, как обычная. Она не является мерой инерции. Это коэффициент, характеризующий состояние частицы в данной энергетической зоне, т.е. характеризующий взаимодействие частицы периодическим потенциалом решётки. Эффективная масса может меняться, может быть меньше 0. Частицу с отрицательной массой рассматривают, как частицу с положительной массой и положительным зарядом, т.е. положительную квазичастицу (дырки).

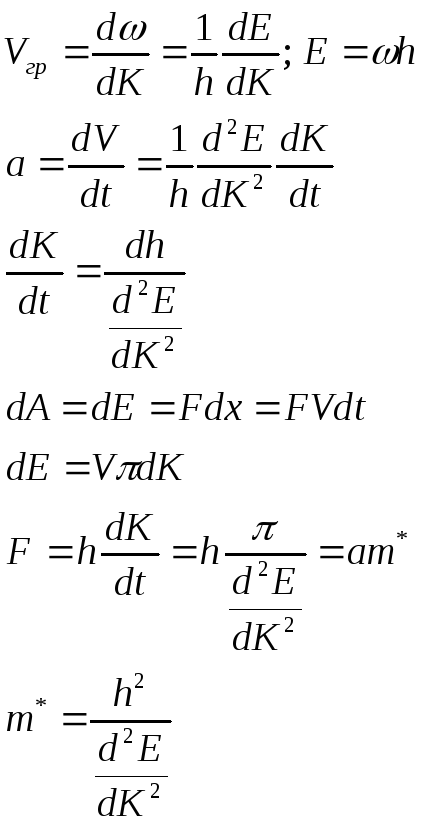
В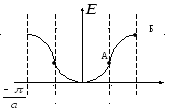общем случае для электрона, находящегося в периодическом поле зависимости энергии отkможет быть сложной. Но в областиk=0 эта зависимость является параболической. По мере приближенияkк зоне Бриллюэна зависимость Е(k) будет отличаться от параболы.

По мере удаления от начала координат зависимость Е(k) отличается от параболы нарастание скоростиvзамедляется,m^*электрона увеличивается. В точке А.

При переходе через точку А m^*меняет знак т.е. при дальнейшем увеличенииkскорость электрона, хотя направление внешней силы остаётся неизменным. В точке В скорость равна 0, хотя импульс электрона достигает максимального значения. В этой точке электрон испытывает отражение от решётки иkменяется отдо. При решении задач на движение частицы, в периодической кристаллической решётки получаемое решение описывается при помощи данной структуры энергетических уровней. Совокупность дисперсных уровней называется энергетической зоной. В каждой такой зоне находится одинаковое число уровней. Все энергетические зоны отдалены друг от друга запрещёнными зонами наивысшая заполненная зона валентная, а следующая за ней заполняемая энергетическая зона – зона проводимости.