Лекция 1

1. Элементы квантовой механики

2. Введение в статистическую физику

3. Введение в физику твёрдого тела

4. Введение в физику полупроводников

5. Контактные явления

Повторить:

1. Корпускулярно-волновой дуализм света (дифракция, интерференция, поляризация, длина волн Дебройля).

2. Строение атома (теории Бора, полная энергия в атоме водорода).

3. Волновая ф-я частиц, свойства волновой ф-ии.

4. Понятие плотности вероятности и самой вероятности нахождения частицы. Условие нормировки волновой ф-ии.

5. Основные правила квантовой механики. Принцип неопределённости Гейзенберга.

Корпускулярно волновая природа света.

Волновые свойства света подтверждают следующие его свойства:

1. Дифракция

2. Интерференция

3. Поляризация

Корпускулярные свойства подтверждаются следующими положениями:

1. Закономерностями в спектре излучения абсолютно твёрдого тела.

2. Явлением фотоэффекта (уравнениями Эйнштейна, з-и Сталетова).

- уравнение Эйнштейна

где - работа выходаиз металла

- постоянная Планка

- частота излучения света.

3. Давление света.

4. Эффекты Комптона – изменение длины волны света при его рассеивании на частицы (электрон, протон).

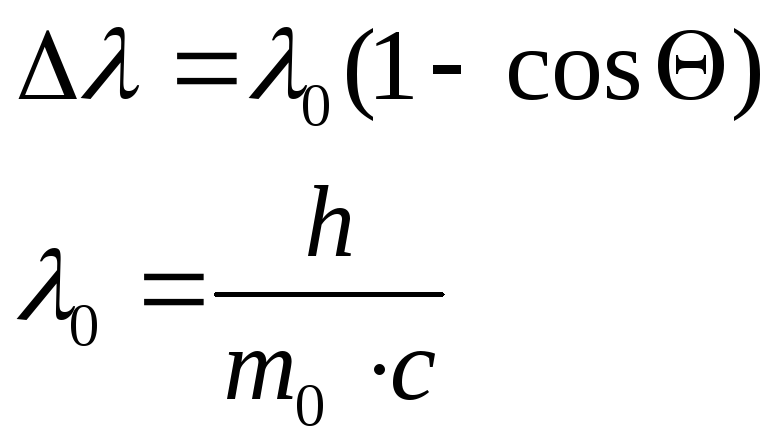
- изменение длины волны

- Комптоновская длина волны для

- угол рассеивания.

Квантовые свойства света подтверждаются излучением света порциями – квантами.

ħ

ħ=

Связь между волновыми и квантовыми свойствами света.

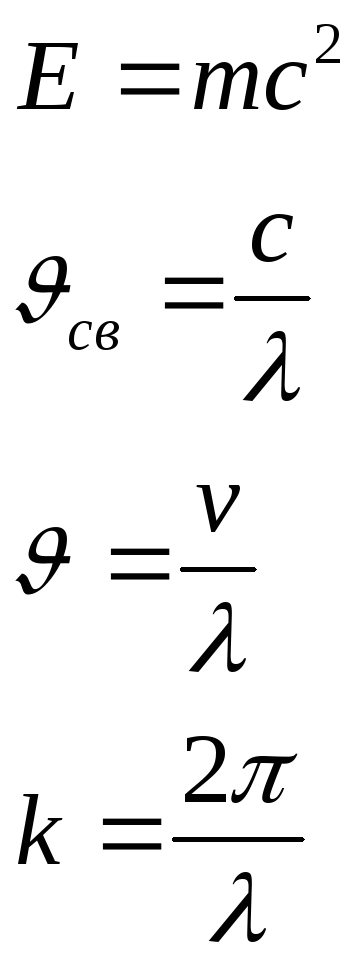
- волновое число

Импульс ħħ

ħ - волновой вектор.

Строение атома. Теория Бора.

Модели Резерфорда. Планетарная модель атома. Постулаты Бора т. к. классическая физика в данном случае даёт неверный результат.

Постулаты Бора:

1. Условия стационарности

2. Условия стационарности частот

3. Условие Бора-Зомерфельда

ħ

- главное квантовое число

- момент импульса электрона

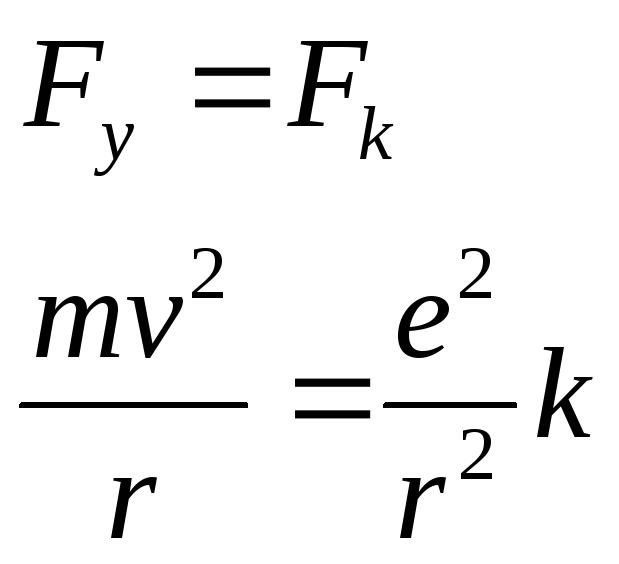
k=1/4εε₀π

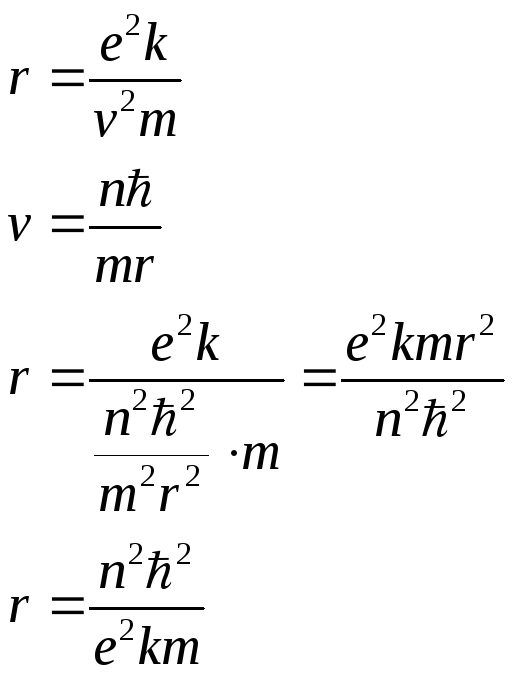
Рассмотрим полную энергию в атоме водорода

Где потенциальная энергия.

Потенциальная энергия заряженной частицы в поле другой частицы или в электрическом поле имеет вид:

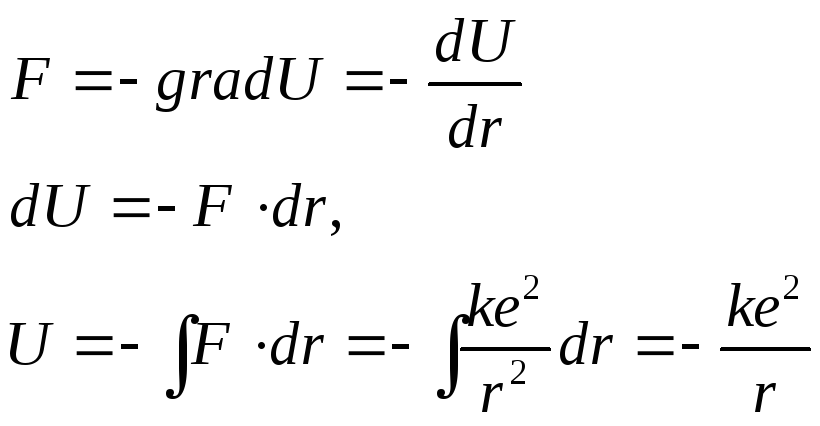
- потенциал.

Потенциальная энергия определяется координатами тела в системе с точностью до некоторой произвольной постоянной.

Электрон в атоме водорода находится в связанном состоянии, поэтому потенциальная и полная энергии имеют отрицательный знак. Чтобыстал свободным, необходимо совершить работу, т. е. затратить энергию ионизации.

Для атома водорода при n=1находится на основном энергетическом уровне, т. е. атом находится в невозбуждённом состоянии.

При n=1 энергия ионизации равна 13,56 эВ.

Энергия электрона в атоме водорода величина квантованная.

Для водородоподобного иона энергия ионизации равна

- зарядовое число

Волновые свойства вещества.

Гипотеза деБройля.

Волны деБройля.

Элементы квантовой механики.

Исходя их того, что свет имеет двойственную природу, т. е. обладает как волновыми, так и корпускулярными, французский физик деБройль выдвинул гипотезу о том, что материя тоже обладает двойственной природой. Это предположение было подтверждено опытами Томсона и ______ опытным путём.

- для нерелятивистского случая (близк. не дляскор. света).

- деБройлеровская длина волны.

Волновые свойства частиц описываются с помощью свойств волн деБройля. Простейшие волны деБройля можно записать через волновую функцию.

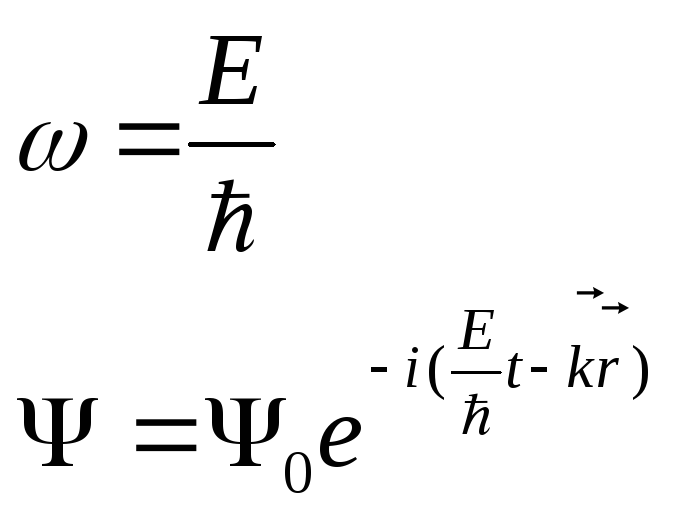
Сама волновая функция физического смысла не имеет, она носит вероятностный характер. Физический смысл имеет квадрат волновой функции.

Зная плотность вероятности для данной частицы, мы можем найти вероятность нахождения частицы в объёме .

Функция считается нормированной, если по всему объёму выполняется условие:

Волновая функция определяет все свойства частиц. Зная волновую функцию можно найти энергию частицы (или спектр энергии), вероятность нахождения частицы в определённом объёме, плотность вероятности.

Однако при этом теряется смысл в понятиях координаты и траектории частицы, поэтому для микрочастиц справедлив принцип неопределённости Гейзенберга.

Чем точнее определяется координата, тем менее точно описывается импульс квантовой частицы.

Свойства волновой функции.

1. Волновые функции, характеризующие частицы, на бесконечности обращаются в 0.

2. На границах функции должны быть гладкими, т. е. сами функции и их производные слева и справа от границы должны быть равны.

3. Принцип суперпозиции. Если получаем несколько решений для волновой функции, то конечное решение – сумма всех решений.