5. Бесконечно малая величина

В теории числовых последовательностей важную роль играет бесконечно малая величина.

Последовательность называется бесконечно малой величиной, если она сходящаяся и её предел равен нулю:

.

Пример 5.1. Последовательность , где – произвольное число, является бесконечно малой величиной:

.

Пример 5.2. Последовательность –бесконечно малая величина:

.

Отметим два важных свойств бесконечно малых величин.

Свойство 5.1. Сумма двух бесконечно малых величин является бесконечно малой величиной.

Следствие 5.1. Сумма любого конечного числа бесконечно малых величин является бесконечно малой величиной.

Свойство 5.2. Произведение бесконечно малой величины на ограниченную величину является бесконечно малой величиной.

Связь между сходящейся последовательности, её пределом и бесконечно малой величины приводится в следующей теореме.

Теорема 5.1. Для того, что последовательность являлась сходящейся с пределом равным , необходимо и достаточно, чтобы имело место представление

,

где – некоторая бесконечно малая величина.

6. Свойства сходящихся последовательностей

Всюду в этом пункте будем предполагать, что последовательности и являются сходящимися и имеют конечные пределы:

.

Теорема 6.1. Предел постоянной величины равен самой постоянной величине:

.

Теорема 6.2. Постоянный множитель можно вынести за знак предела:

или

.

Теорема 6.3. Предел суммы двух последовательностей равен сумме пределов этих последовательностей:

или

.

Теорема 6.4. Предел разности двух последовательностей равен разности пределов этих последовательностей:

или

.

Теорема 6.5. Предел произведения двух последовательностей равен произведению пределов этих последовательностей:

или

.

Теорема 6.6. Предел частного двух последовательностей равен частному пределов этих последовательностей, если предел знаменателя не равен нулю:

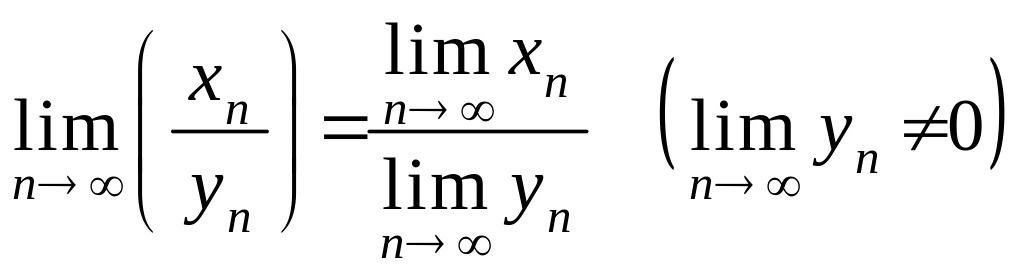
или

.

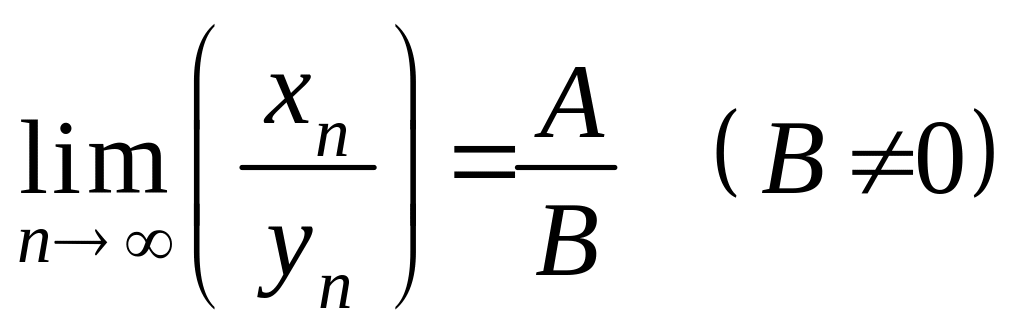7. Предельный переход в неравенствах

Теорема 7.1. Пусть все члены сходящейся последовательности удовлетворяют неравенству . Тогда и предел этой последовательности удовлетворяет этому неравенству

.

Замечание 7.1. Если для членов сходящейся последовательности выполняется строгое неравенство , то предел этой последовательности может равняться этому числу: .

Пример 7.1. Все члены последовательности -строго положительны (строго отрицательны), т.е. . Однако

.

Теорема 7.2. Пусть все члены сходящихся последовательностей и удовлетворяют неравенству . Тогда их пределы удовлетворяют этому неравенству

.

Замечание 7.2. Если для членов сходящихся последовательностей и выполняется строгое неравенство , то их пределы могут быть равными

.

Теорема 7.3. Пусть все члены сходящейся последовательности принадлежат промежутку , т.е. . Тогда и предел этой последовательности принадлежит этому промежутку, т.е. .

Замечание 7.3. Если все члены сходящейся последовательности принадлежат промежутку , т.е. , то предел этой последовательности может не принадлежать этому промежутку, т.е. могут выполняться нестрогие неравенства .

Теорема 7.4. Пусть все члены последовательностей , и удовлетворяют неравенствам . Тогда если последовательности и сходятся и имеют общий предел , то последовательность также сходится и имеет место равенство

.