4.2Пример определения вертикального перемещения поперечного сечения (прогиба) балки с помощью линий влияния

Определить прогиб δ_с в середине пролета балки АВ при различных вариантах ее нагружения (рис. 53).

Балка имеет постоянное по ее длине сечение с моментом инерции J относительно оси изгиба, модуль упругости материала Е.

Решение.

Построение линии влияния δс.

Выберем систему координат: начало координат в точке А, ось «х» направим вправо, ось «δ_с» - вниз (рис. 53 в).

Необходимо рассмотреть два участка - от А до С и от С до В. Помещая единичный груз в произвольное положение поочередно на каждом участке и определяя прогиб δ_с, можно было бы получить уравнения линии влияния δ_с для каждого участка.

Однако в данном случае целесообразно воспользоваться принципом взаимности перемещений и рассматривать уравнения линии влияния на каждом участке как уравнения изогнутой оси балки на этих же участках от добавочной силы Р₂=1, приложенной в рассматриваемом сечении С балки (см.п.4.1.).

Получить уравнения изогнутой оси балки для каждого участка можно путем интегрирования ее дифференциального уравнения:

±EJ·(d²δ_с/dx²) = M(x),

где EJ – жесткость балки; M(x) – изгибающий момент; d²δ_с/dx² – вторая производная от прогиба δ_с.

Знак изгибающего момента М (х) не зависит от направления оси перемещений «δ_с», а знак второй производной зависит. Вторая производная положительна, если в сторону положительного направления оси «δ_с» обращена вогнутость кривой, и отрицательна, если выпуклость.

Оставим ранее принятое правило знаков для изгибающего момента – он положителен, если изгибает балку выпуклостью вверх.

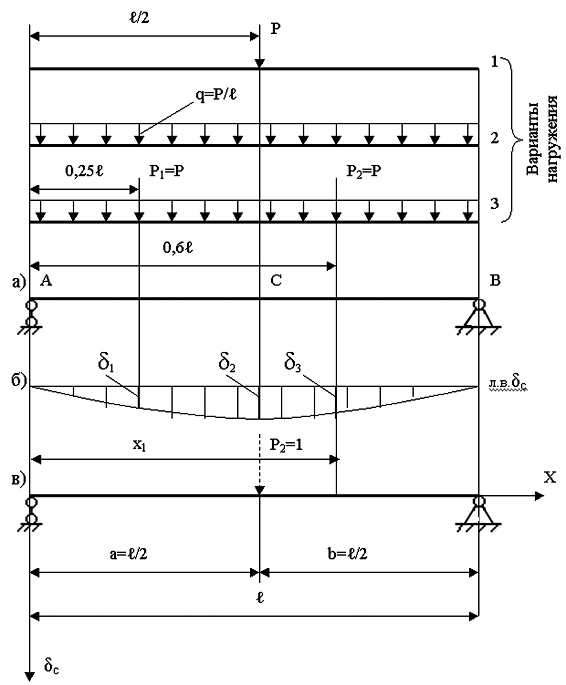
Рис. 53

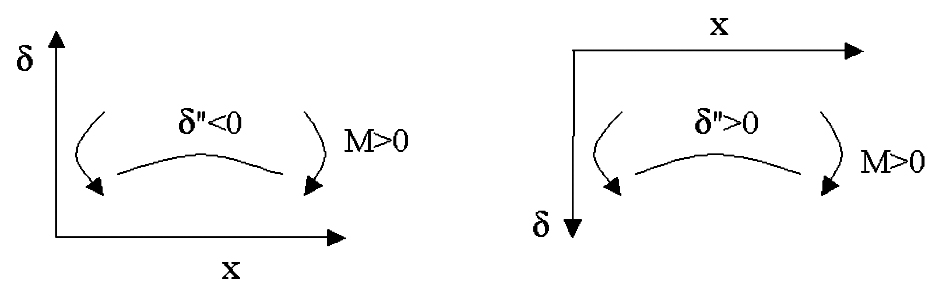
Рис. 54

На рис. 54 показано, что при направлении оси «δ» вниз знаки М и δ совпадают. В этом случае дифференциальное уравнение изогнутой оси балки запишется в виде:

EJδ_c" = M (x).

Изгибающие моменты в произвольных сечениях рассматриваемых участков (с координатами x и x₁), вызванные добавочной силой Р₂=1, приложенной в сечении «С», будут равны (рис. 53 в):

для левого участка М (x) = -R_A·x = -b·x/ℓ;

для правого участка M (x₁) = - R_A·x₁+(x₁-a) = -b·x₁/ℓ+(x₁-a).

Дифференциальные уравнения для каждого участка запишутся в виде:

E·J·δ_c" = -b·x/ℓ, E·J·δ_c" = -b·x₁/ℓ+(x₁-a).

В результате интегрирования этих уравнений, определения постоянных интегрирования и некоторых преобразований получим уравнения изогнутой оси балки для каждого участка, которые в то же время являются уравнениями линий влияния для этих участков:

для левого участка 0 ≤ x ≤ a

δ_с = 1/(EJ)·[-bx³/(6ℓ)+bx/(6ℓ)·(ℓ²-b²)],

для правого участка a ≤ x ≤ ℓ

δ_с = 1/(EJ)·[-bx₁³/(6ℓ)+(x₁-a)³/6+bx₁/(6ℓ)·(ℓ²-b²)].

Эти уравнения являются уравнениями линии влияния прогиба в любом сечении балки, положение которого определяется отрезками «a» и «b».

Для рассматриваемого сечения «С» при a = b =ℓ/2 уравнения линии влияния δ_с получат вид:

для левого сечения a ≤ x ≤ ℓ/2

δ_с = 1/(48EJ)·(3ℓ²x-4x³),

для правого сечения ℓ/2 ≤ x ≤ ℓ

δ_с = 1/(48EJ)·[8(x₁-ℓ/2)³- 4x₁³ +3ℓ² x₁].

Линия влияния δ_с изображена на рис. 53 б.

Определение прогиба δс.

Для определения прогиба δ_с линию влияния δ_с строить не нужно. Необходимые ординаты и площади линии влияния под погонной нагрузкой следует определять по ее уравнениям.

а) При первом варианте нагружения прогиб δ_с = P·δ₂.

Ордината δ₂ находится по уравнению линии влияния для любого участка:

δ₂ = ℓ³/(48EJ).

Следовательно, δ_с = Pℓ³/(48EJ).

б) При втором варианте нагружения прогиб δ_с = q·w,

где w – площадь всей линии влияния.

Линия влияния симметрична относительно сечения «С». Поэтому, воспользовавшись уравнением для левого участка, получим:

_ℓ/2

w = 2∫ [1/(48EJ)·(3ℓ²x-4x³)]dx = 5ℓ⁴/(384EJ).

⁰

Следовательно, δ_с =5qℓ⁴/(384EJ) = 0,625Pℓ³/(48EJ).

в) При третьем варианте нагружения прогиб

δ_с = P₁·δ₁+ P₂·δ₃+q·w₁ = P·(δ₁+ δ₃)+q·w₁,

где w₁ – площадь левой половины линии влияния, расположенная под погонной нагрузкой.

Воспользовавшись первым уравнением линии влияния δ_с для определения δ₁ при x = 0,25ℓ и вторым уравнением для определения δ₃ при x = 0,6ℓ, получим:

δ₁ = 0,6875ℓ³/(48EJ), δ₃ = 0,944ℓ³/(48EJ).

Используя первое уравнение линии влияния δ_с, получим:

_ℓ/2

w₁ = ∫ [1/(48EJ)·(3ℓ²x-4x³)]dx = 5ℓ⁴/(768EJ).

⁰

q·w₁ = 0,3125Pℓ³/(48EJ).

Следовательно, δ_с = Pℓ³/(48EJ)·(0,6875+0,944+0,3125) = 1,944Pℓ³/(48EJ).