3.7Пример расчета сварной фермы

Требуется спроектировать сварную ферму пролетом 8 м, высотой 3 м. Длина панели 2 м. Неподвижная нагрузка Р составляет 10 т, подвижная нагрузка Т_max = 5 т, Т_min = 0,1 т и находится внизу. Расстояние между подвижными грузами t равно 2 м (рис. 43). Материал фермы низкоуглеродистая сталь ВСт.3, допускаемое напряжение []_р = 16 кг/мм².

Рис. 43

Построение линии влияния продольных усилий в стержнях фермы

В начале определим реакции на опорах. Для этого примем следующую систему координат: начало координат на левом конце фермы, ось х направлена вправо, ось z – вверх. Движение единичного груза примем по нижнему поясу (рис. 44).

;

;

;

.

Рис. 44

Линии влияния для стержней поясов, параллельных оси X (рис. 45)

Это стержни 0-1, 1-3.

Рассмотрим стержень 0-1. Построим фиктивный стержень 2-2'. Проведем сечение I-I, которое пересекает три стержня. В этом случае для стержня 0-1 моментной точкой является точка 2.

Разбиваем ферму на две части слева и справа от моментной точки. Поставим единичный груз справа от моментной точки. В равновесии рассмотрим левую часть фермы (рис. 46 а).

.

Отсюда

.

Это уравнение справедливо на участке   l:

при x = ,

при x = l = 0.

l

Рис. 45

Поставим единичный груз слева от моментной точки, в равновесии рассмотрим правую часть фермы (рис. 46 б).

.

Отсюда

.

Это уравнение справедливо на участке 0  x  :

при x = 0 = 0,

при x = .

Линия влияния N_0-1 показана на рис. 45.

а) б)

Рис. 46

Рассмотрим стержень 1-3. Проведем сечение 2, которое пересекает три стержня. Для стержня 1-3 моментной точкой является точка 4. Поставим единичный груз справа от точки 4 и рассмотрим в равновесии левую часть фермы (рис. 47 а).

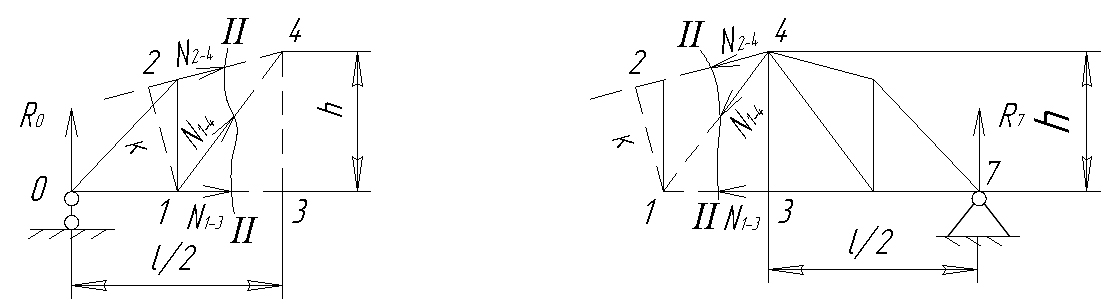
а) б)

Рис. 47

.

Отсюда

.

Это уравнение справедливо на участке  x  l:

при x = ;

при x = l = 0.

Поставим единичный груз слева от точки 4 и рассмотрим в равновесии правую часть фермы (рис. 47 б).

.

Отсюда .

Это уравнение справедливо на участке 0  x  :

при x = 0 = 0,

при x = .

Линия влияния N_1-3 показана на рис. 45.

Линии влияния для стержней поясов, непараллельных оси х

Это стержни 0-2, 2-4.

Для построения линий влияния стержня 0-2 нужно взять проекцию сил на ось Z. (сечение I-I, рис. 46 а). Линия влияния состоит из трех участков: справа от точки 1, слева от опоры (точка 0) и в пределах разрезанной панели 0-1.

Поставим единичный груз справа от точки 1. В равновесии рассмотрим левую часть фермы (рис. 46 а).

.

Отсюда

.

Это уравнение справедливо на участке  x  l.

; ; .

При x = l = 0.

При x = .

Поставим единичный груз слева от точки 0 (за пределы опоры). В равновесии рассмотрим правую часть фермы (рис. 46 б).

.

Отсюда

.

Это уравнение справедливо на участке -  x  0.

При x = 0 = 0.

Нулевую точку 0 соединяем с ординатой -1,01 и получаем третий участок линии влияния .

Линия влияния N_0-2 показана на рис. 45.

Рассмотрим стержень 2-4. Для построения линий влияния продольного усилия в этом стержне воспользуемся сечением II-II, которое пересекает три стержня. Для стержня 2-4 имеется моментная точка 1. Поставим единичный груз справа от моментной точки 1 и рассмотрим в равновесии левую часть фермы (рис. 47 б).

,

отсюда

.

Это уравнение справедливо на участке  x  l.

При x = .

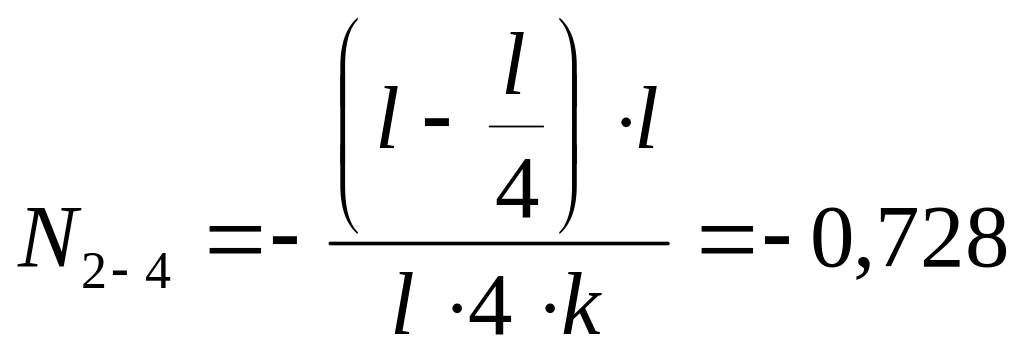При x = l .

Поставим единичный груз слева от моментной точки 1 и рассмотрим в равновесии правую часть фермы.

.

Отсюда

.

Это уравнение справедливо на участке 0  x  .

При x =0 N_2-4=0.

При x = .

Плечо момента N_2-4k находится из треугольника 1' 4 1 (рис. 48).

k = 1'1 = сsin;  = 90° –  – ;

; ; ;  = 34°;

; ;

; ;  = 21°;

 = 90° – 21° – 34° = 35°; sin = 0,573;

к = сsin = 3,60,573 = 2,06.

Рис. 48

При x = l N_2-4 = .

При x = .

Линия влияния N_2-4 показана на рис. 45.