2.3. Расчёт основных характеристик вариационного ряда

Статистический анализ вариационных рядов распределения предполагает расчёт характеристик центра распределения, его структуры, оценку степени вариации и дифференциации изучаемого признака, изучение формы распределения.

В качестве показателей центральной тенденции распределения используются: среднее арифметическое значение, мода и медиана. Основными показателями являются: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Для характеристики структуры распределения: медиана, квартили, децили и прочие перцентили.

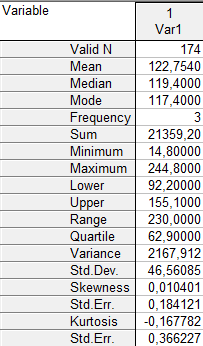
Рис. 2.22. Основные характеристики вариационного ряда

Приведем формулы полученных статистических характеристик:

Valid N — объем выборки (число единиц в совокупности).

Mean — средняя арифметическая:

,

где - значение признака у i-й единицы совокупности;

n – объем совокупности (Valid N).

Median — медиана:

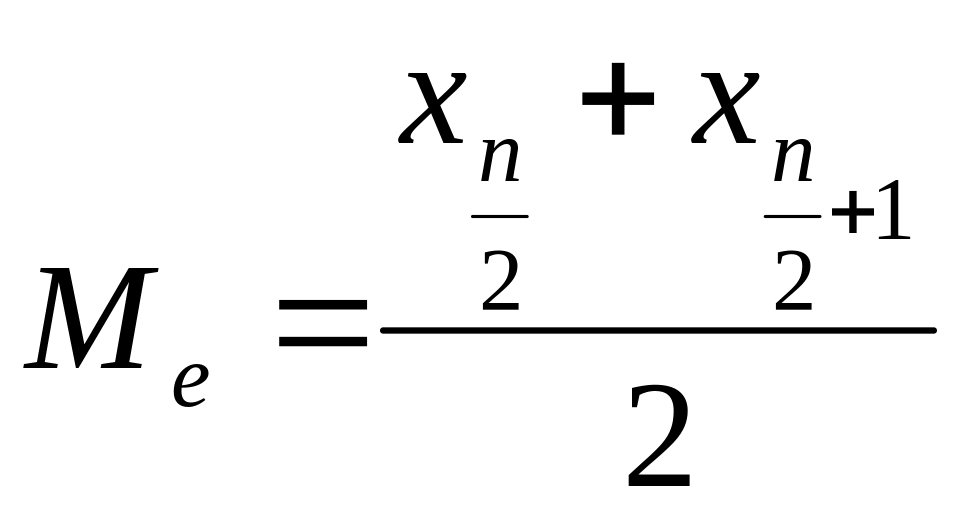, если n — четное,

, если n — нечетное.

Так как n=174, т.е. четное,

Mode —мода (М_о) определяется непосредственно по исходным данным.

Frequency – частота модального значения.

Sum — сумма значение признака в совокупности: .

Variance — дисперсия: ,

где - средняя арифметическая.

Coef.Var. – коэффициент вариации: .

Standard deviation — среднеквадратическое (стандартное) отклонение:

.

Standard (Standard error) — средняя (стандартная) ошибка выборки:

.

Minimum — минимальное значение признака в совокупности: x_{min .}

Maximum — максимальное значение признака в совокупности: x_max.

Range — размах вариации: R = x_max – x_min.

Lower (Lower quartile) — нижний (первый) квартиль:

Upper (Upper quartile) — верхний (третий) квартиль:

Quartile (Interquartile range) — межквартальный размах: Q₃ – Q_1.

Skewness — асимметрия:

.

Std.err. (Standardized skewness) — стандартизованная асимметрия:

Kurtosis — коэффициент эксцесса (куртозис):

.

Std.err. (Standardized kurtosis) — стандартизованный куртозис.

Сравним значение показателей, полученных в системе и рассчитанные вручную по сгруппированным данным.

Таблица 2.1

Сравнение статистических показателей, рассчитанных различными способами

№	Название показателя	Значения в ППП STATISTICA	Значения ручного расчета по сгруппированным данным
1	Средняя арифметическая	122,754	123,22
2	Медиана	119,4	120
3	Мода	117,4	108
4	Дисперсия	2167,912	2236,768
5	Верхний квартиль	155,1	155,8
6	Нижний квартиль	92,2	92,6

2.4. Сглаживание эмпирического распределения. Проверка гипотезы о законе распределения.

Процедура выравнивания, сглаживания анализируемого распределения заключается в замене эмпирических частот теоретическими, определяемыми по формуле теоретического распределения, но с учётом фактических значений переменной. Для проверки статистической гипотезы о законе распределения будем использовать универсальный критерий χ  -критерий Пирсона.

Мы определили, что наиболее подходящее для нас число интервалов равно 8. Проверим гипотезу о нормальном, логарифмически нормальном и прямоугольном распределениях.

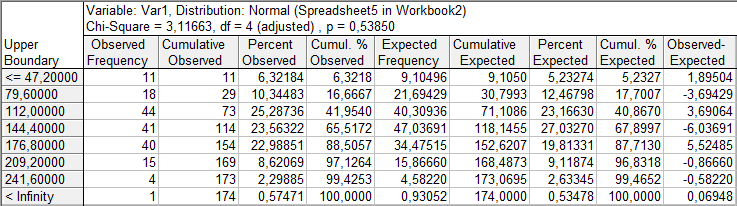
Рис. 2.23. Проверка гипотезы о нормальном распределении переменной Var1.

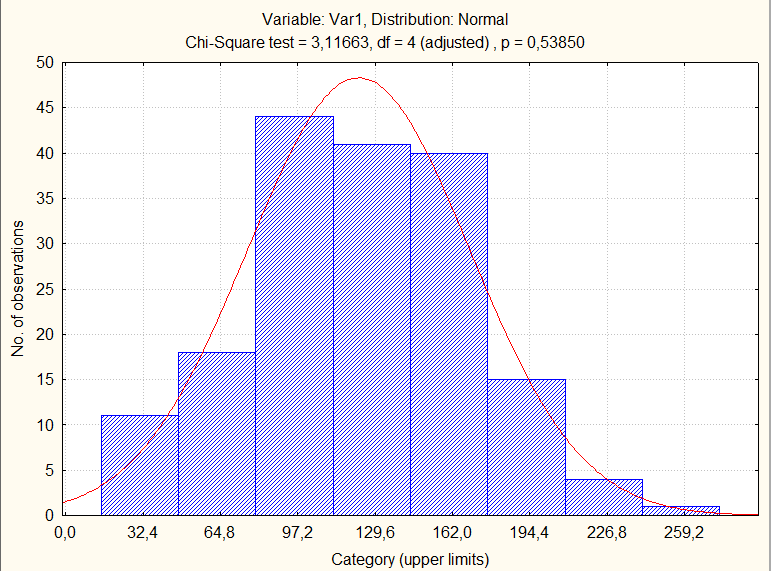
Рис. 2.24. Гистограмма и расчетная кривая нормального распределения для переменной Var1.

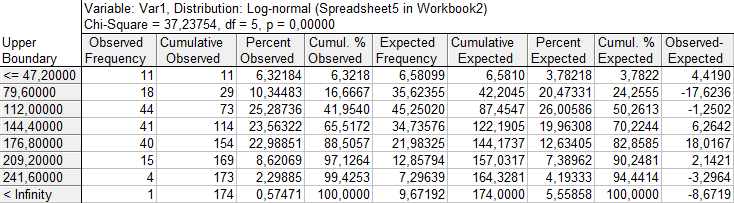
Рис. 2.25. Проверка гипотезы о логарифмически нормальном распределении переменной Var1.

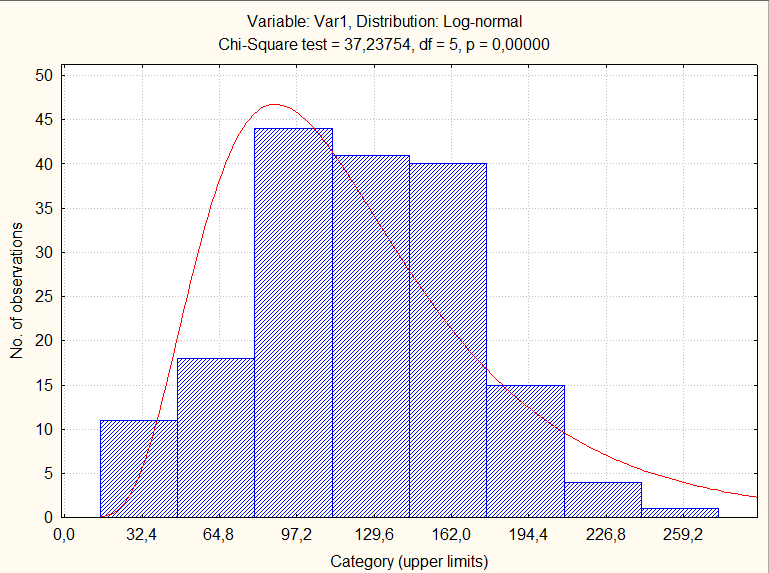
Рис. 2.26. Гистограмма и расчетная кривая логарифмически нормального распределения для переменной Var1.

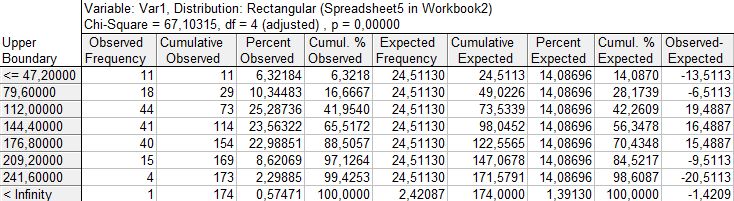
Рис. 2.27. Проверка гипотезы о прямоугольном распределении переменной Var1.

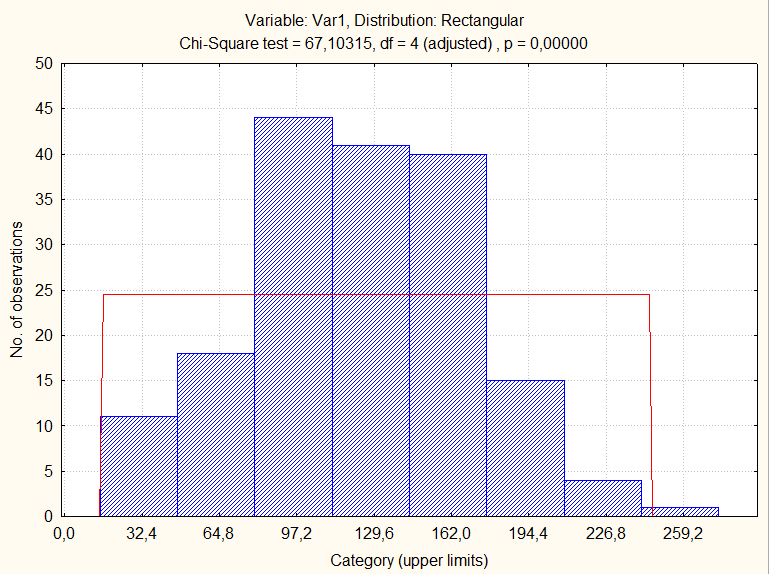
Рис. 2.27. Гистограмма и расчетная кривая прямоугольного распределения для переменной Var1.

Подведем итог решения задачи сглаживания, представив его в таблице.

Таблица 2.2

Результаты решения задачи сглаживания

Тип распределения	Число степеней свободы r	Расчетное значение критерия 20	Табличное значение критерия 2α,r	P(2α,r≥20) (расчетное значение уровня значимости)
Нормальное	4	3,11663	9,488	0,53850
Логнормальное	5	37,23754	11,07	0,0000
Прямоугольное	4	67,10315	9,488	0,0000