§ 4. Динамика газов

Элементы теории движения реальных газов

При движении газа на каждый его объем будут дейст­вовать не только те силы, которые характерны для стати­ки, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеаль­ного газа этими дополнительными силами будут силы инер­ции, а для реального газа — силы инерции и трения (вяз­кости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих мате­матических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне огра­ниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Та­ким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.

Уравнение Бернулли. В практических условиях крайне распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизмен­ным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).

Для несжимаемого газа ( = const) уравнение Бернул­ли при условии, что все его члены отнесены к единице объ­ема, имеет вид

gz +р +²/2 = const. (14)

В соответствии с этим величина р является статическим давлением, величина gz — геометрическим давлением, величина ²/2 — динамическим давлением.

Уравнение Бернулли представляет собой закон сохра­нения энергии, поскольку сумма р + gz характеризует потенциальную, а величина ²/2 — кинетическую энергию.

Как отмечалось выше, в металлургической теплотехни­ке в подавляющем большинстве случаев пользуются дав­лением, избыточным над атмосферным. Поэтому полезно уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью _в, по которому движется газ плотностью _г. Принимая плотности газа и воздуха неизменными, напи­шем уравнение Бернулли и для газа и воздуха примени­тельно к сечениям канала z₁ и z₂.

Уравнение для газа

Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)

Вычитая из первого второе, получаем уравнение Бер­нулли для газа в избыточных давлениях:

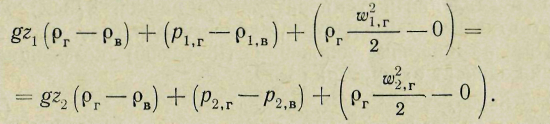
₍₁₅₎

Если перейти к ранее принятому обозначению через h, то уравнение можно соответственно переписать в таком виде:

(15)

Однако равенство h_1 = h_2 строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Но если по каналу перемещается реальная (вязкая) жид­кость (газ), то часть энергии тратится на преодоление различных сопротивлений и происходит потеря энергии.

В этом случае при движении от сечения I к сечению II

h_1 = h_2 + h_потерь (16)

и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жид­кости (газа) для различных сечений канала сумма давле­ний всех видов является постоянной».

Рассмотрим, что представляет собой потерянное давле­ние, входящее в уравнение Бернулли.

При движении реального газа часть его энергии расхо­дуется на преодоление различных сопротивлений.

Различают потери на трение и потери на преодоление местных сопротивлений. Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при пово­роте канала или усложнении его сечения (трубчатый пу­чок). Величину потерь напора выражают в долях динами­ческого давления.

Потери на трение Л_тр можно определить по формуле (Па)

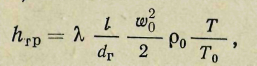(17)

где  — коэффициент трения; l — длина канала, м; d_г — гидравлический диаметр канала, м (для некруглого сече­ния канала d_г =4F/П, F — площадь сечения канала, м²; П — периметр канала, м); ₀ и ₀ — плотность и скорость жидкости (газа) при нормальных условиях, т. е. при атмос­ферном давлении и температуре Т₀, равной 273 К; Т — действительная температура жидкости или газа, К.

При ламинарном движении (Rе < 2300) коэффициент трения зависит от критерия Rе

 = 64/Rе. (18)

При турбулентном движении коэффициент трения зави­сит не только от критерия Rе, но и от относительной шеро­ховатости стенки канала (/d), равной отношению абсо­лютной шероховатости  (в мм) к диаметру канала d:

_(18)

При приближенных практических расчетах коэффици­ент трения  можно принимать постоянным и равным для кирпичных каналов 0,05, для металлических 0,04.

Потери на преодоление местных сопротивлений опреде­ляются по формуле (Па)

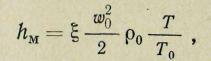
где  — коэффициент местных сопротивлений. Его величи­на зависит от формы местного сопротивления и, как прави­ло, определяется опытным путем.

Важнейшим расчетом, который выполняется для подав­ляющего большинства печей, является определение сум­марных потерь давления на пути движения дымовых газов от печи до дымовой трубы. Суммарные потери исполь­зуются при определении размеров дымовой трубы, кото­рая рассчитывается из условия, что разрешение, создавае­мое дымовой трубой, должно быть по абсолютной величине больше суммы всех сопротивлений, возникающих в дымо­вом тракте печи (см. том 2-й настоящего издания).

Таким образом, уравнение (закон) Бернулли находит очень широкое применение. Наряду с уравнением Бернул­ли важную роль в гидро- и аэродинамике играют также уравнение сплошности и уравнение импульсов Эйлера.

Уравнение сплошности. В практических условиях наи­более распространенными являются такие процессы, при которых масса газа, протекающая по какому-то объему, остается неизменной. При этом, естественно, масса газа, втекающая в объем в единицу времени, должна быть рав­на массе вытекающего газа.

Следовательно, можно написать, что т₁ = т₂, или, учи­тывая, что масса есть произведение скорости, сечения по­тока и плотности, получаем

₁f1₁ = ₂f₂₂.

При условии постоянства плотности (₁ = ₂) последнее выражение принимает вид

₁f1 = ₂f₂. (19)

Если в качестве скорости принимать среднюю скорость потока, то выражение (19) применимо для практических расчетов при течении в трубах и каналах, причем средняя скорость потока определяется как частное от деления се­кундного объема среды, проходящего через данное сече­ние, на величину площади сечения, т. е.

 = V/f.

Уравнение импульсов Эйлера. Уравнение импульсов (количеств движения) Эйлера имеет важное значение для некоторых практических расчетов. Это уравнение приме­нимо к какому-то воображаемому контуру, выделенному в общем потоке газа, через боковую поверхность которого ни движения, ни массообмена не происходит.

В подобном контуре под действием внешних сил (в по­токе газа под действием давления) происходит изменение количества движения газа. Если изменение импульсов проходящего газа и изменение внешних сил отнести к единице времени, то теорема импульсов Эйлера может быть сфор­мулирована следующим образом: «Изменение импульса всех сил, приложенных к газу, проходящему через выделен­ный контур, равно результирующей внешних сил, действу­ющих на данный контур».

Записывается это уравнение так:

(m) = P. (20)

Применение уравнения импульсов будет проиллюстри­ровано ниже при рассмотрении струйных аппаратов. Рас­четы инжекторов и эжекторов с использованием выраже­ний, полученных на основании применения уравнения им­пульсов Эйлера, приведены во 2-м томе настоящего изда­ния.

Применение уравнения Бернулли

Трудно назвать раздел механики газов, где не исполь­зовалось бы в той или иной мере уравнение Бернулли. По­знакомимся лишь с некоторыми наиболее важными случа­ями применения этого уравнения.

Истечение газов через отверстия и насадки

Истечение газов через отверстия и насадки наблюдает­ся при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истече­ние. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.

Отверстия с острыми краями. Положим, что из сосуда очень больших размеров, давление в котором р₁, газ выте­кает через отверстие сечением f₀ в среду с давлением р₂. Для определения скорости истечения газа ₂ напишем уравнение Бернулли для сечений I и II (рис. 9). Поскольку температура газа неизменна, постольку h_г1 = h_г2. В этом случае, пренебрегая потерями, можно написать

₍₂₁₎

_{Вследствие большого размера сосуда можно принять 1 = 0}

Тогда

Отсюда

(22)

В силу инерции частичек истекающего газа сечение струи f меньше сечения отверстия f₀. Отношение f/f₀ =  называется коэффициентом сжатия струи. Скорость ₂ фактически относится не ко всему сечению отверстия f₀, а лишь к сечению струи f. Для определения расхода газа че­рез отверстие f₀ найдем V = ₂f. Но f = f₀ следовательно,

(23)

С учетом гидродинамических потерь при истечении че­рез отверстие выражение (23) принимает вид (м³/с)

(24)

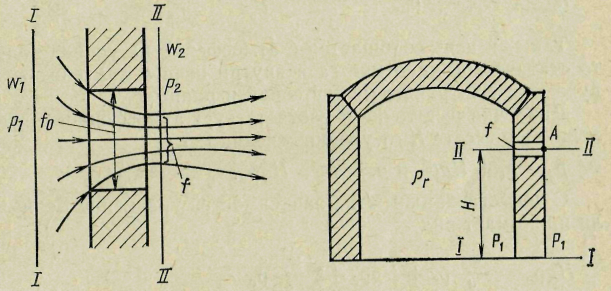
Рис. 9. Истечение газа из отвер- Рис. 10. Истечение из отверстия в

стия в тонкой стенке стечке печи

Смысл коэффициентов  и , ясен из следующего при­мера.

Истечение из отверстия в стенке печи (рис. 10) — весь­ма распространенный на практике случай. Рассмотрим подобный случай истечения (с учетом потерь) из отверстия сечением f, расположенного на высоте Н от уровня пода печи. Напишем уравнение Бернулли для сечения I и точки А в сечении II:

Скорость движения газов в отверстии ₂ много больше скорости ₁; исходя из ₂  ₁, принимаем ₁ = 0.

Как следует из изложенного выше, потери на местные сопротивления могут быть определены как

Так как печь сообщается с атмосферой на уровне пода, то статическое давление газа внутри печи и давление воз­духа снаружи равны между собой и равны р₁.

Давление р₂ в точке А соответствует атмосферному дав­лению на высоте H от уровня сечения I, т. е.

С использованием этих зависимостей уравнение Бернул­ли принимает вид

или

Отсюда

(25)

Величина учитывает гидравлическое сопро­тивление отверстия, через которое происходит истечение.

Количество истекающей из рассматриваемого отвер­стия среды (м³/с) V = ₂f₂, где f₂ — сечение струи, м².

Но если использовать понятие коэффициента сжатия струи  = f₂/f, то

.

Произведение  =  называют коэффициентом расхода.

Истечение через насадки. Насадком называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадка обычно составляет 3—4 его диаметра. Ко­личество газа, протекающее через насадок, при прочих равных условиях зависит от формы входных кромок и формы самого насадка. Рассмотрим насадки трех видов, представленные на рис. 11. Пользуясь уравнением (22), получим для них следующие расчетные формулы: для насадки с открытыми кромками

(26)

(27)

Для насадков с закругленными кромками и диффузора

(28)

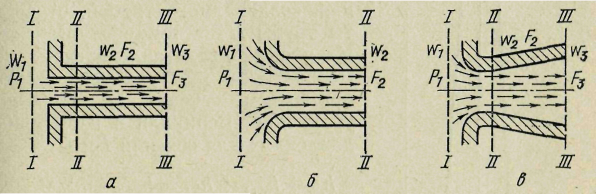
Рис. 11. Истечение газа через цилиндрические насадки:

а — с открытыми кромками; б — с закругленными краями; в — диффузор

Для этих насадков в сечении ІІІ сечения струи и отвер­стия равны друг другу и поэтому здесь  = 1,0. Сравнение выражений (26), (27) и (28) показывает, что наибольший расход при одинаковом значении р₁ — р₂ и при одинаковом минимальном сечении насадков получается при истечении газа через диффузор, так как площадь выходного сечения у диффузора F₃ больше, чем у насадков других типов. Угол конусности диффузора не должен превышать 6—7° во избежание отрыва потока от стенок диффузора.

Истечение газов через небольшие отверстия в стенках печи (например, гляделки) можно рассчитывать по фор­мулам для цилиндрического насадка.

Д ымовая труба. Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение соз­дается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному, как будет показано ниже, разностью плотностей холодного наружного воздуха и горячих газов. Найдем зависимость разреже­ния, создаваемого трубой, от высо­ты трубы Н и температуры газов. На рис. 12 представлена схема ды­мовой трубы. За уровень отсчета принимаем сечение ІІ. Напишем уравнение Бернулли в избыточных давлениях для сечений І и ІІ:

h_г1 + h_ст1 + h_д1 = h_ст2 + h_д2 + h_пот.

Труба в сечении II сообщается с атмосферой, поэтому h_ст2 = 0. Из приведенного выше уравнения сле­дует, что статическое давление в основании трубы

h

Рис. 12 Схема дымовой трубы

_ст1 = – h_г1 + h_д2 – h_д1 + h_пот.

Ввиду незначительных скоростей движения газов в тру­бе величины потерь, выражаемые в правой части приведен­ного выше уравнения тремя последними членами, значи­тельно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, статическое давление в основании трубы будет отрицательным, т. е. там будет разрежение. Умножив правую и левую части последнего уравнения на минус единицу, получаем

– h_ст1 = h_раз = h_г – (h_д2 – h_д1) – h_пот. (29)

Потери давления в трубе h_пот складываются из потерь на трение h_тр и потерь, возникающих при выходе газов из трубы в атмосферу и равных h_д2. Учитывая, что коэффи­циент местного сопротивления на выходе из трубы ра­вен единице ( = 1), можно написать, что

h_пот = h_тр + h_д2.

Вследствие этого уравнению (29) можно придать сле­дующий вид:

h_раз = h_г + h_д1 – 2 h_д2 – h_тр. (29)

Для того чтобы получить окончательное выражение для h_разр, в уравнение (29) необходимо подставить все входя­щие в него величины. Температура газов по высоте дымо­вой трубы и ее сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения га­зов в дымовой трубе определяются по средней температу­ре по высоте трубы. Величина геометрического давления h_г, входящего в уравнение (29), выражается уравнением (13). Динамические давления будут соответственно равны

Потери давления на трение находят по уравнению

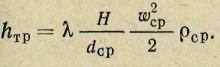
Подставив в уравнение (29') значения h_г, h_д1, h_д2, h_тр и выразив их через скорости и плотности при нормальных условиях (₀ и ₀) по указанным выше выражениям, окон­чательно получаем (Па)

(30)

где h_разр — действительное разрежение в основании дымо­вой трубы (сечение I), Па; и — плотность соответст­венно воздуха и газов при нормальных условиях, кг/м³; d_ср — средний по высоте диаметр трубы, м; ₀₁ и ₀₂ — скорость газов в сечениях I (в основании трубы) и II (в устье трубы) при 0°С, м/с; _0ср — средняя скорость га­зов по высоте трубы при 0°С, м/с; t_в — температура окружающего воздуха, °С; — средняя температура газов по высоте трубы, °С; t_г1 и t_г2 — температура газов в сечениях I и II, °С.

Если учесть, что

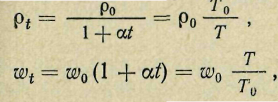
где Т₀ = 273 К, то выражение (30) может быть переписано следующим образом:

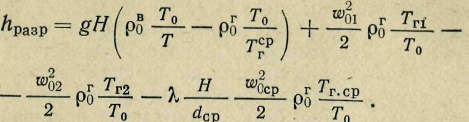
Отсюда

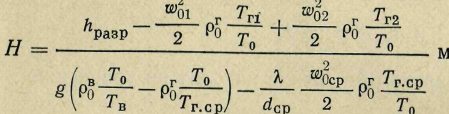
(30)

В расчетах разрежение в основании дымовой трубы принимают обычно с запасом, равным h_разр = 1,3 h_пот. Ве­личина  h_пот представляет собой суммарные потери напо­ра на пути движения газов от печи до основания дымовой трубы.

При расчете дымовой трубы внутренний диаметр в устье ее d_у (на выходе) принимают, исходя из скорости газов, равной 3—10 м/с (при скорости выхода газов, не меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы d₀ прини­мают в 1,5 раза больше внутреннего диаметра устья трубы d_у, т. е. d₀ = 1,5d_у.

По условиям выполнения кладки d_у для кирпичных труб не должен быть меньше 0,8 м.

Падение температуры газов на 1 м высоты трубы при­нимается для кирпичных и железобетонных 1,0—1,5 °С, а для металлических 3—4°С. Ориентировочно высота тру­бы может быть определена по уравнению (30) без трех последних его членов.

Подсчитав сумму потерь всех видов на пути движения газов от печи до основания дымовой трубы, по уравнению (30') находят расчетную высоту трубы Н. Независимо от расчета высота дымовой трубы по правилам сантехники должна быть не менее 16 м и в 2 раза выше самого высо­кого здания, находящегося в радиусе 100 м вокруг трубы.

Сверхзвуковое движение газов

Общие сведения. В металлургических печах в ряде слу­чаев применяются такие устройства, в которых газ движется с весьма высокой скоростью, превышающей иногда скорость звука.

С огласно современным представлениям, скорость звука определяют формулой Лапласа, по которой

(31)

где א = с_р/с_V — коэффициент, равный отношению теплоем­кости среды при постоянном давлении к теплоемкости при постоянном объеме.

Применяя формулу Клапейрона (р/ = RТ), получим

(32)

Из выражения (32) следует, что скорость звука зависит только от температуры и физических свойств газа.

С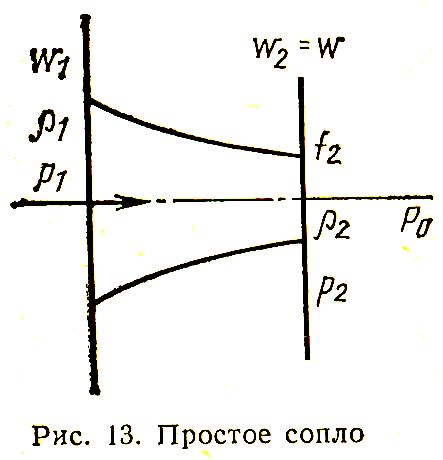 корость газа может быть мень­ше скорости звука, больше и равна ей. Если скорость движения газа станет равной местной скорости звука, то такая скорость газа  = а называется критической. Сечение потока, в котором достигается это равенство, называется критическим. Критическим называются также давление, плотность и температура в этом сечении.

Отношение скорости движения газа  к местной скорости звука а называется числом (кри­терием) Маха М. При М<1 поток дозвуковой, при М = 1 звуковой и при М>1 сверхзвуковой.

Движение газа по трубе переменного сечения. Посте­пенно сужающаяся по ходу газа труба называется конфузором, а постепенно расширяющаяся — диффузором. Соот­ношение между скоростью движения газов и сече­нием канала (трубы) переменного сечения описывается уравнением Гюгонио, которое в конечных разностях может быть представлено следующим образом:

Величины  и F представляют собой малые прираще­ния (изменения) соответственно скорости движения среды и сечения канала, по которому эта среда движется.

Из этого уравнения можно сделать следующие выводы:

1. если М<1, то знак  противоположен знаку F. Следовательно, при дозвуковом движении газа (как и не­сжимаемой жидкости) с возрастанием площади сечения трубы скорость движения уменьшается, и наоборот;

2. если М>1, то знак  одинаков со знаком F. Сле­довательно, при сверхзвуковом движении в суживающейся трубе движение замедляется, а в расширяющейся трубе ускоряется. Это происходит в результате того, что при расширении газа плотность его настолько сильно уменьшается, что произведение F уменьшается, несмотря на увеличение F. Это в свою очередь приводит к увеличению , поскольку F = const;

3. если М=1, то F = 0 и соответствующее сечение будет критическим. Критическое сечение является минимальным, так как при подходе к нему дозвуковой поток замедляется, а сверхзвуковой ускоряется.

Простое сопло. Большую роль в технике играют устрой­ства, обеспечивающие создание потока газа, истекающего с большой скоростью. Основным элементом таких устройств является сопло (рис. 13). При истечении газов через сопла происходит резкое изменение давления и, следовательно, объема. Поэтому уравнения движения и истечения, приве­денные выше для несжимаемого газа, здесь неприемлемы.

Скорость истечения газов из сопла может быть дозву­ковой, равной скорости звука и сверхзвуковой.

При установившемся движении в каждом сечении соп­ла поток газов будет характеризоваться определенными ме­стными значениями скорости движения , давления Р, плотности  и температуры Т.

Если в данном сечении скорость движения газа  рав­на скорости распространения звука, то скорость движения газа, давление и другие параметры, соответствующие этому условию, будут иметь критические значения _кр и P_кр.

Как видно из уравнения Гюгонио, особенностью газов является то, что при переходе от звуковой скорости движе­ния к сверхзвуковой изменяется характер зависимости ме­жду давлением Р и плотностью  и соответственно между сечением F и скоростью движения .

В дозвуковой области давление и плотность газов свя­заны между собой так, что увеличение сечения канала вы­зывает соответствующее уменьшение скорости , и наобо­рот. При сверхзвуковых скоростях связь между Р и  та­кова, что увеличение F сопровождается увеличением скорости .

Максимальная скорость истечения газа из обычного (суживающегося) сопла может достигать только критического значения, но не выше, независимо от давления перед соплом. Критические параметры истечения из простого соп­ла могут быть определены из следующих выражений.

Критическая скорость истечения, м/с

Критическое давление, Па

Критическая масса газа, кг/с

Коэффициент א = 1,4 для двухатомных газов и א = 1,3 для сжатого пара.

С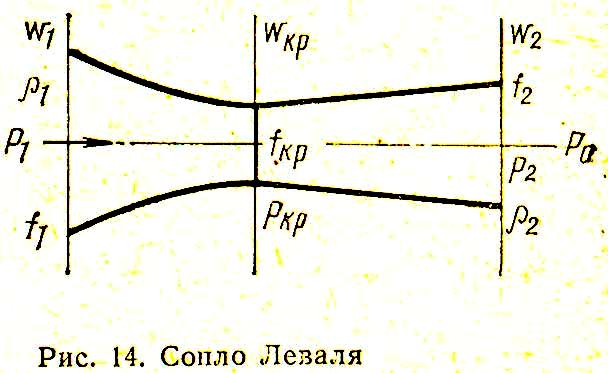 опло Лаваля. Сверхзвуковая скорость >_зв может быть получена в сопле, состоящем из суживающейся и рас­ширяющейся частей (рис. 14). Такое сопло называется соплом Лаваля по имени его создателя. Сопло Лаваля рассчитывают таким обра­зом, чтобы скорость в са­мом узком критическом се­чении его была критичес­кой, а в расширяющейся части превосходила звуко­вую, постепенно возрастая по мере приближения к выходному отверстию сопла. Если ско­рость в критическом сечении f_кр сопла будет меньше крити­ческой, то в расширяющейся части она будет уменьшаться, а не увеличиваться, т. е. будет изменяться так же, как и в обычном сопле.

В сопле Лаваля выравнивание (уменьшение) давления в критическом сечении до Р_с происходит не за соплом, а в расширяющейся части сопла, и сопровождается увеличени­ем скорости истечения. Соответственно возрастает кинети­ческая энергия струи, которая используется для соверше­ния полезной работы. В этом преимущество сопла Лаваля перед обычным соплом.

Максимум полезно используемой энергии достигается при условии, что длина расширяющейся части сопла Лава­ля не больше и не меньше, чем это требуется для полного выравнивания (уменьшения) давления. Если это условие не выполняется, то эффективность применения сопла Лаваля уменьшается.

Характеристики истечения из сопла Лаваля могут быть определены из следующих выражений:

критическая скорость, м/с

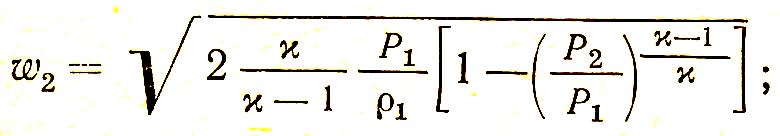
критическая масса, кг/с

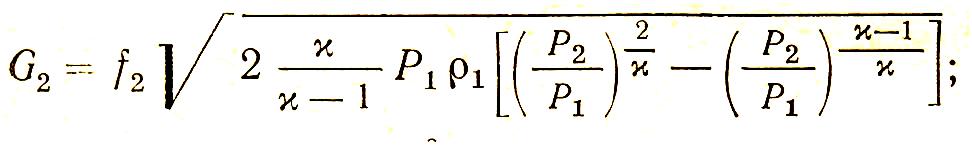
площадь сечения, м²

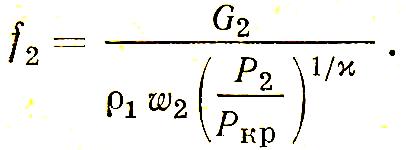
Сопла Лаваля широко применяются при создании кис­лородных и газокислородных фурм для конвертеров, мар­теновских и двухванных печей.