§ 3. Теплопроводность

Теплопроводность при стационарном состоянии

При стационарном тепловом состоянии температура с тече­нием времени остается неизменной. В практике металлурги­ческой теплотехники подобные случаи передачи тепла теплопроводностью встречаются при передаче тепла через плоские стенки.

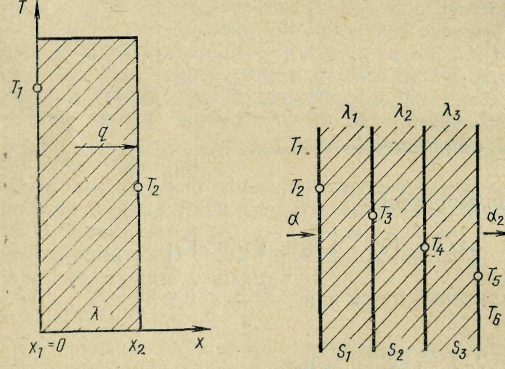
Рис. 27. Плоская однослой- Рис. 28. Плоская трехслойная

ная стенка стенка

Однослойная стенка. Чтобы получить выражения, позво­ляющие определить распределение температур в стенке и количество передающегося через нее тепла, необходимо ре­шить дифференциальные уравнения теплопроводности со­вместно с краевыми условиями I рода. Применительно к этому случаю (рис. 27), когда тепло передается через стенку толщиной s = х₂ — x₁ от поверхности с температурой Т₁ к поверхности с температурой Т₂, изменение температу­ры по толщине стенки описывается уравнением

₍₄₀₎

а плотность теплового потока, проходящего через стенку, Вт/м²

Следует заметить, что выражение (40) представляет собой уравнение прямой линии, следовательно, распростра­нение температуры в однослойной плоской стенке при  = const имеет прямолинейный характер. Если , зависит от температуры, то распределение температуры имеет криво­линейный характер, причем кривая выгибается вверх, когда  увеличивается с повышением температуры, и вниз, когда , уменьшается с увеличением температуры.

Многослойная стенка. Рассмотрим плоскую стенку, со­стоящую из трех слоев (рис. 28). Можно принять любое число слоев, причем каждый из них может обладать свои­ми физическими свойствами. Чтобы получить выражение, позволяющее определить количество тепла, проходящее через многослойную стенку, необходимо помнить, что для стационарного процесса плотность теплового потока, про­ходящего через каждый слой, одинакова, т. е. q₁ = q₂ = q₃ = q

Как видно, знаменатель данного уравнения представля­ет собой сумму тепловых сопротивлений отдельных слоев.

Передача тепла от более нагретого газа к менее нагре­тому через плоскую стенку. На практике часто приходится определять количество тепла, которое требуется передать от одного газа к другому (или к жидкости) через стенку (многослойную или однослойную), т. е. решать задачу, по­добную изображенной на рис. 28.

Поскольку рассматривается стационарное тепловое со­стояние, постольку температуры теплоотдающего газа Т₁ и тепловоспринимающего газа Т₆, так же как и величины Т₂, Т₃, Т₄, и Т₅ остаются во времени неизменными. Соблюдение постоянства температуры окружающей среды — есть усло­вие, присущее граничным условиям III рода. Процесс теп­лообмена определяется в данном случае коэффициентами теплоотдачи ₁ и ₂.

Плотность теплового потока, который отдается более нагретым газом, может быть определена по выражению

Плотность теплового потока, который передается через стенку, была определена в предыдущем разделе:

Плотность теплового потока, передаваемого от стенки к менее нагретому газу:

При стационарном состоянии

После сложения этих трех уравнений, получаем

(41)

Как указывалось выше, величина обратная коэффициен­ту теплоотдачи 1/₁ (или s/), выражает тепловое сопро­тивление. Следовательно, знаменатель уравнения (41) представляет собой сумму тепловых сопротивлений различ­ных звеньев передачи тепла. Уравнение (41) может быть записано в виде:

q = K(T₁ – T₆),

Величину К называют коэффициентом теплопередачи. Напомним, что разница между терминами «теплоотдача» и «теплопередача» заключается в том, что термин теплоотда­ча применим для какой-либо одной ступени передачи тепла, например от газа к стенке, от стенки к газу и т. п. Термин «теплопередача» применим для обозначения более сложно­го процесса передачи тепла, включающего в себя несколько ступеней этого процесса, например передачу тепла от газа к газу через стенку, где наблюдаются три ступени теплоперехода: от газа к стенке, через стенку и от стенки к друго­му газу. Подобным же образом можно объяснить различие между коэффициентом теплоотдачи  и коэффициентом теплопередачи K.

Теплопроводность при нестационарном состоянии

Основные решения. Как отмечалось выше, при нестаци­онарном состоянии с течением времени происходит измене­ние температуры тела, т. е. дТ/д  0.

Подобное изменение температуры тела возможно, когда тело остывает или когда оно нагревается. На практике это широко распространенный процесс нагрева металла. Реше­ние дифференциального уравнения теплопроводности со­вместно с краевыми условиями представляет собой весьма сложную математическую задачу, поэтому остановимся лишь на решении при краевых условиях III рода, получив­шем наибольшее практическое распространение. На прак­тике часто встречаются печи, в которых нагрев металла происходит при неизменной температуре рабочего простран­ства. Некоторые печи с изменяющейся температурой по длине печи можно условно разделить на расчетные участки с приближенно неизменной температурой в пределах каж­дого участка и к каждому из них применить решения, полу­ченные при краевых условиях III рода.

Приведем без вывода окончательное решение дифферен­циального уравнения теплопроводности для бесконечной плиты при краевых условиях III рода, которое имеет сле­дующий вид:

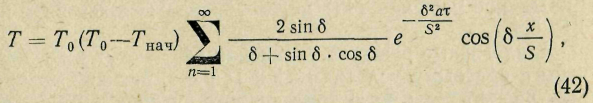
где Т₀ — температура печи (среды), К; Т_нач — температура металла в начальный момент нагрева, К; а — коэффициент температуропроводности, м²/с;  — время нагрева (или ох­лаждения) тела, с; S — расчетная толщина нагреваемого тела, м;  — величина, зависящая от S/;  — коэффици­ент теплоотдачи (от газа к металлу), Вт/(м²К); х — рас­стояние от центра тела до той точки, для которой определя­ют температуру Т, м.

А нализируя уравнение (42), можно видеть, что темпера­тура нагрева металла Т зависит от трех безразмерных ком­плексов: критериев а/S², S/ и х/S и что уравнение (42) может быть заменено критериальным уравнением следую­щего вида:

(43)

где  — безразмерный температурный критерий; Т₀ — тем­пература среды (печи); Т_нач и Т_кон —температура нагрева­емого тела соответственно начальная и конечная.

В зависимости от условий решения уравнения Т_кон мо­жет представлять собой как конечную температуру поверх­ности тела (при х/S = 1), так и конечную температуру в центре тела (при х/S = 0).

Безразмерный комплекс а/S² представляет собой из­вестный критерий Фурье, а безразмерный комплекс S/ — критерий Био.

Безразмерный геометрический симплекс х/S определяет собой местоположение точки в теле, для которой определя­ют температуру. Так, для центра нагреваемого тела x = 0 и х/S = 0, для поверхности тела x = S и х/S = 1.

Таким образом, решая уравнение (43) для поверхности тела (х/S = 1), получаем температурный критерий

Характер нагрева тел существенно зависит от критерия Вi. Данное решение (42) целесообразно использовать при Вi>0,5.

Аналогичные решения уравнения (42) могут быть полу­чены с краевыми условиями I и II рода, расчеты по кото­рым рассмотрены во II томе данного учебника. Для инже­нерных расчетов зависимости типа (43) обычно представляются в графическом виде.

В металлургии и машиностроении распространенным процессом нестационарной теплопроводности является про­цесс нагрева металла перед обработкой давлением и для термической обработки. В процессе нагрева изменяется не только температура металла, но и его физические свойства (, с, ) и коэффициент теплоотдачи. Однако аналитические решения типа (42) и (43) получены при условии, что эти величины не изменяются во времени. Поэтому для получе­ния надежных результатов весь период нагрева целесооб­разно разбивать на интервалы и в пределах каждого интер­вала температуру усреднять и по ней выбирать и опреде­лять , с,  и .

Метод конечных разностей. Некоторые практические задачи могут быть решены с применением приближенных методов. К их числу отно­сится метод конечных разностей (метод Шмидта), который часто при­меняют для нагрева или остывания огнеупорной футеровки печи. Этот метод основан на том, что в дифференциальном уравнении теплопро­водности бесконечно малые величины заменяют малыми, но уже ко­нечными величинами. Дифференциальное уравнение теплопроводности для одномерного потока имеет вид

Если бесконечно малые приращения dТ, d, dх заменить конечными малыми прираш.ениями, то уравнение можно записать так:

(44)

В этом уравнении конечные малые приращения представляют со­бой:  — отрезок времени, в течение которого происходит изменение температуры T, с; x — толщину элементарного слоя нагреваемого материала, на протяжении которой происходит изменение температуры в течение времени , м.

Для практического применения этого метода необходимо выбрать значения величин x и 

Для определения x всю стенку конечной толщины следует произ­вольно разделить на некоторое число равных по толщине слоев и таким образом определить величину x, выраженную в метрах, а следователь­но, и число слоев m = x/x. Отсчет слоев x следует вести от более нагретой стороны стенки к менее нагретой: x₁ — слой, расположенный непосредственно у более нагретой поверхности, а x_m — слой, располо­женный около холодной поверхности.

Отрезок времени  определяют в зависимости от величины по вы­ражению

где а — коэффициент температуропроводности, м²/с.

Задача расчета заключается в том, чтобы установить распределение температур в стенке по истечении определенного времени , прошедше­го с момента начала нагрева. Таким образом, частное n = / дает число расчетных отрезков времени, из которых ₁ — начальный, а _к — конечный отрезок времени, ч.

В начале нагрева, т. е. в начале отрезка, характеризующего вре­мя ₁ температура нагреваемого тела в пределах каждого отрезка x считается неизменной. Обычно нагрев подобного рода происходит с од­ной стороны, поэтому для расчета необходимо знать температуру по­верхности или закон изменения температуры поверхности с более нагре­той стороны. Как более нагретой, так и менее нагретой поверхности стенки приписывается роль отдельных очень тонких слоев. Так, индекс x₀ обозначает более нагретую поверхность, прилегающую к слою x₁. Индекс x_m+1 обозначает менее нагретую поверхность.

Методом конечных разностей наиболее часто пользуются для расче­та прогрева стен в печах периодического действия, где зачастую пред­ставляется возможным задать изменение температуры поверхности стен с внутренней стороны, поскольку температура собственно поверхности бывает близка к температуре раскаленных газов, заполняющих печь. Однако температуру поверхности можно определить и расчетным путем по выражению

(45)

где — температура поверхности x_m+1 в любой отрезок времени, К; Т₂ — температура газовой среды, омывающей стенку, К;  — коэффициент теплоотдачи от стенки к газу, Вт/(м²К);  — коэффици­ент теплопроводности материала стенки, Вт/(мК).

Температура в каждом слое стенки в определенный отрезок време­ни может быть определена как полусумма температур предыдущего и последующего слоев в предшествующий отрезок времени. Так

Таким образом, можно получить распределение температур в плос­кой однородной стенке. Однако если стенка состоит из двух различных материалов (например, шамот + тепловая изоляция), то в расчет необ­ходимо внести некоторые дополнения. Первую стенку х, как и в случае однородной стенки, следует разделить на определенное число элемен­тарных слоев x, причем отрезки времени должны быть получены из уравнения

Эти отрезки времени должны быть, естественно, одинаковыми для первой и второй стенок, т. е. _x = _y =.

Поэтому толщину элементарных слоев второй стенки у нельзя вы­бирать произвольно; ее следует определять по выражению

,

где а_х и а_y — коэффициенты температуропроводности первой и второй стенок, м²/с.

В пределах каждой из двух стенок температуру элементарных сло­ев определяют, как и для однородной стенки. Температуру поверхности также определяют по выражению (45).

В месте соприкосновения двух материалов температуру можно най­ти по выражению

(46)

где — температура в месте соприкосновения двух стенок в про­извольный отрезок времени _n, К; и — температура соприкасающихся слоев соответственно первой и второй стенок в тот же отрезок времени _n, К; R₁ = x/₁ и R₂ = x/₂ — тепловое сопротив­ление элементарных слоев первой и второй стенок.

Выяснив таким образом, каково распределение температур, можно путем простого арифметического усреднения получить среднюю темпе­ратуру прогретой стенки и определить то количество тепла, которое аккумулировано стенкой в процессе нагрева. Аккумулирование тепла кладкой является очень важной расходной статьей теплового баланса периодически действующих печей.