2.7. Кинематика вращательного движения.

2.7.1. Угловая скорость.

ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.

В

Рис. 2.14

качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)

Для характеристики вращательного движения вводится понятие угловой скорости

.

Вектор направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).

Модуль вектора угловой скорости равен . Если = const, то такое движение называется равномерным, при этом , следовательно и при t₀ = 0 получаем .

Если ₀ = 0, то  = ·t или .

Таким образом, при равномерном движении  показывает на какой угол поворачивается тело за единицу времени. Размерность угловой скорости []=рад/сек.

Равномерное вращение можно характеризовать периодом вращения T, под которым понимают время, за которое тело делает один полный оборот, т.е. поворачивается на угол 2. В этом случае , следовательно .

Ч

Рис. 2.15

астота вращения (число оборотов в единицу времени): =1/T=/2. Отсюда =2.

Дополнение 1.

Поворот тела на некоторый малый угол d можно задать в виде отрезка, длина которого равна d, а направление совпадает с осью, вокруг которой совершен поворот. Таким образом, повороту тела можно приписать некоторое численное значение и направление. При этом направление вектора можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом ( , , и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный: .

2.7.2. Угловое ускорение.

Вектор угловой скорости может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется о величине), так и за счет поворота оси вращения в пространстве (в этом случае изменяется по направлению). Для характеристики быстроты изменения вводится физическая величина , называемая угловым ускорением.

ОПРЕДЕЛЕНИЕ: Средним угловым ускорением называется величина , где t – промежуток времени за который произошло изменение угловой скорости.

ОПРЕДЕЛЕНИЕ: Мгновенным ускорением называется величина равная ;

Если направление оси вращения в пространстве постоянно, то угловая скорость изменяется только по величине и в этом случае .

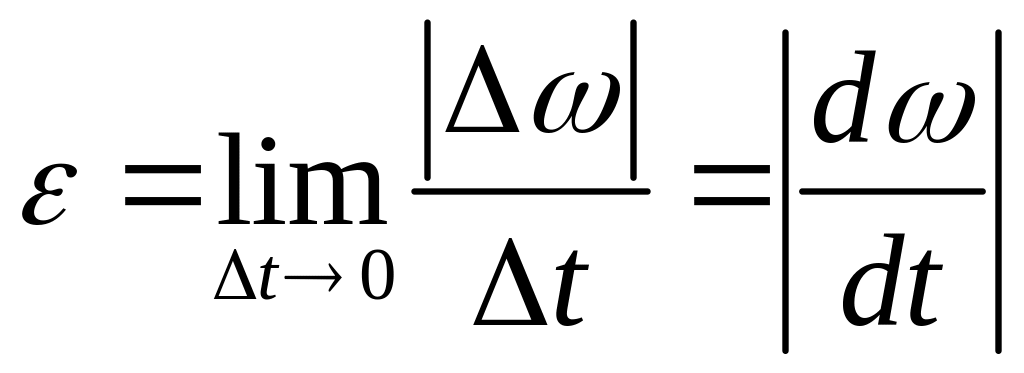Если под  понимать проекцию вектора на направление , то последняя формула примет вид . Здесь  – алгебраическая величина и

если  , то >0 (векторы и одного направления),

е

Рис. 2.16

сли  , то <0 (  ).

1) Если >0  вращение равноускоренное (  ) (рис. 2.16).

2) Если <0 – (  ) (рис. 2.16).

В системе СИ []=рад/с².

Для равноускоренного движения:

Следовательно,  = ₀ + ·(t - t₀). При t₀ = 0 получаем  = ₀ + ·t.

Тогда ;

Окончательно

(2.6)

Теперь установим