Лекция 7. Понятие линейного преобразования. Собственные векторы.

Пусть переменные х₁ и х₂ связаны с переменными х₁^/ и х₂^/ следующими формулами

, (1)

тогда матрица А = называется матрицей линейного преобразования вектора

в вектор , или точки М(x₁, x₂) в базисе , в точку М’(x’₁, x’₂) в базисе .

Матричная запись линейного преобразования

.

В общем случае отличаются по величине и по направлению. Важное значение имеют те векторы , которые при линейном преобразовании не меняют прямой, на которой они находились до преобразования.

Определение. Ненулевой вектор ē называется собственным вектором линейного преобразования с матрицей А, если он переводится этой матрицей в вектор, коллинеарный вектору ē, то есть,

Аē = λē, (2)

где λ- некоторое число, которое называется собственным значением матрицы А.

Пусть вектор ē {m;n}, тогда из матричного уравнения (2) следует

или

(3)

Вопрос о существовании собственных векторов сводится к вопросу о существовании ненулевого решения линейной относительно m и n, однородной системы (3).

Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю:

=0 (4)

Уравнение (4) называется характеристическим уравнением.

В матричном виде уравнение (4):

| A – λ E | = 0. (5)

Уравнение (4) может не иметь действительных корней, и тогда собственных векторов с вещественными координатами нет.

Если корни характеристического уравнения вещественные равные, то можно указать собственный вектор.

Если характеристическое уравнение имеет два различных вещественных корня, то можно найти два собственных вектора.

Симметрическое линейное преобразование.

Линейное преобразование называется симметрическим, если его матрица А симметрична:

А = А^т

Для матрицы размера (2 × 2) это условие имеет вид а₁₂ = а₂₁.

Теорема. Собственные значения симметрического линейного преобразования вещественны, а собственные векторы ортогональны.

Теорема о приведении матрицы к диагональному виду.

Пусть матрица линейного преобразования

А = .

Пусть ₁,₂-собственные значения матрицы А, ē₁ {m₁, n₁} и ē₂{m₂, n₂} соответствующие собственные векторы, причем неколлинеарные.

Рассмотрим матрицу из координат собственных векторов:

В= , det(B)0, тогда матрица B^-1AB= .

Преобразование координат при переходе к новому базису (изменение направления осей).

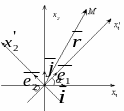Пусть система координат х₁0х₂ определяется ортонормированным базисом . Единичные векторы ē₁ ={m₁, n₁}, ē₂{m₂, n₂} примем за направляющие векторы новых осей координат системы , ē₁ ┴ ē_2.

Пусть новая система координат, определяемая базисом ē_1, ē₂ повернута на угол α относительно старой системы координат, определяемой базисом .

Матрица В = , составленная из координат векторов ē₁ и ē₂, является матрицей перехода к новому базису.

Координаты нового базиса ē₁, ē₂ относительно старого базиса будут:

и, следовательно, матрица перехода к новому базису имеет вид:

B= и B^-1=

В данном случае транспонированная матрица совпадает с обратной.

X=BX‘, =

(5) и (5’)

Полученные формулы (5) и (5^/) являются формулами преобразования координат при повороте осей координат.