Линии (кривые) второго порядка

1. Эллипс. Каноническое уравнение эллипса

Определение 1. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F₁ и F₂ той же плоскости есть величина постоянная, большая, чем расстояние между точками F₁, F₂.

Точки называются фокусами, расстояние F₁F₂ называется фокальным расстоянием. Обозначаем его через 2с. Через 2а обозначим сумму расстояний от любой точки эллипса до фокусов. По определению a > c.

В ыведем уравнение эллипса в прямоугольной системе координат Oxy, связанной с эллипсом. Для этого начало O системы координат поместим в середину отрезка F₁F₂, ось Ox направим по прямой F₁F₂. Такая система координат называется канонической. В выбранной системе координат фокусы имеют координаты F₁(-c, 0) и F₂(c, 0) .

Пусть M(x,y) - произвольная точка плоскости Oxy. По определению 1 точка M принадлежит эллипсу тогда и только тогда, когда

MF₁ + MF₂ = 2c. (1)

Находим

MF₁ = , MF₂ = .

Отсюда получим уравнение эллипса

. (2)

Обозначаем

и найденное выше уравнение запишем в виде

. (3)

Уравнение (3) называется каноническим уравнением эллипса. Отрезки MF₁, MF₂ называются фокальными радиусами точки M.

Замечание 1. Если точки F₁ и F₂ совпадают, то из определения 1 следует, что в этом случае эллипс превращается в окружность радиуса а. При этом уравнение (3) принимает вид x² + y² = a².

2. Исследование эллипса по каноническому уравнению. Эллипса и окружность. Эксцентриситет эллипса.

1. Эллипс не проходит через начало системы координат, так как координаты точки О(0,0) не удовлетворяют уравнению (3).

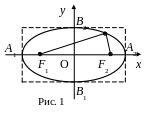
2. Найдем точки пересечения эллипса с осями координат. Для нахождения точки пересечения с осью Ох полагаем в уравнении (3) у = 0 и находим x = a. Таким образом эллипс пересекает ось Ох в точках A₁(-a, 0), A₂(a, 0). Аналогично находим, что эллипс пересекает ось Оy в точках B₁(0,-b), B₂(0, b).

Точки A₁, A₂, B₁, B₂ называются вершинами эллипса, отрезки A₁A₂, B₁B₂ осями эллипса; A₁A₂ =2a, B₁B₂ =2b; числа a, b называются полуосями эллипса. Так как a > b, то A₁A₂ называется большой осью, B₁B₂ - малой осью.

3. Так как все переменные входят в уравнение (3) в четной степени, то вместе с точкой (x, y) эллипсу принадлежат четыре точки (x, y) (с произвольными комбинациями знаков). Таким образом, эллипс симметричен относительно, всех координатных осей Ox, Oy и начала координат. Точка О называется центром эллипса.

4. Из уравнения эллипса находим, . Отсюда следует, что эллипс ограниченная линия, которая находится в прямоугольнике: -a  x  a, -b  y  b (см. рис. 1).

5. Исследуем поведение эллипса в первой четверти. Для этого выразим y из уравнения (3) через x:

.

Отсюда видим, в первой четверти на отрезке [0, a] эллипс является графиком убывающей функции.

6. Любая прямая, проходящая через начало координат, пересекает эллипс в двух точках. Действительно, вертикальная прямая, ось Oy, пересекает эллипс в двух вершинах, любую другую прямую можно задать уравнением y = kx, k  R.

Эллипса и окружность. Эксцентриситет эллипса.

Теорема 1. Любой эллипс, отличный от окружности может быть получен в результате сжатия окружности к диаметру.

Уравнения

(4)

являются параметрическими уравнениями эллипса.

Определение 2. Эксцентриситетом  эллипса называется число, равное отношению его фокального расстоянию с к длине его большей полуоси a: .

Из определения эллипса следует, что 0   < 1. Для окружности эксцентриситет равен нулю.

Так как , то . Из этого соотношения получаем, что чем ближе  к 1, тем меньше отношение b/a, при одинаковых значениях a тем более продолговатый эллипс.