Лабораторна робота № 1 Тема: Побудова множинної лінійної регресійної моделі.
Завдання.
Побудувати модель множинної лінійної регресії, вибравши статистичну вибірку згідно варіанту. Розрахунок параметрів моделі провести за 1МНК. Провести дисперсний аналіз отриманої моделі:
обчислити коефіцієнти множинної детермінації та кореляції і зробити висновки щодо отриманих результатів;
чи адекватною (статистично значимою) є отримана модель;
перевірити гіпотези про значимість всіх коефіцієнтів множинної регресії отриманої моделі;
перевірити гіпотезу про статистичну значимість коефіцієнта детермінації;
побудувати інтервали надійності для всіх коефіцієнтів множинної регресії;
зробити точковий прогноз значення регресанта при значенні регресорів
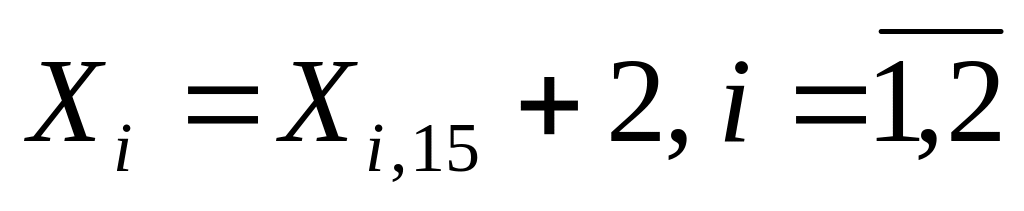
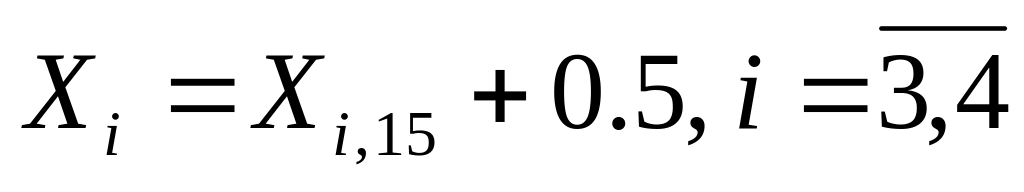та обчислити середню стандартну
(середньоквадратичну) похибку прогнозу;зробити інтервальний прогноз для значень регресанта при значенні регресорів , .
Варіанти завдань.
Залежність між продуктивністю праці Y та фондозабезпеченістю, тис. грн., Х1, стажем роботи в роках Х2, Х3 — плинністю кадрів (у частках), рівнем оплати праці, тис. грн/рік — Х4 наведено в таблицях:
№ з/п |
Y |
X1 |
X2 |
X3 |
X4 |
1 |
14,85 |
60 |
30 |
0,15 |
5,0 |
2 |
11,94 |
48 |
19 |
0,02 |
3,1 |
3 |
8,03 |
39 |
8 |
0,14 |
4,7 |
4 |
7,11 |
28 |
18 |
0,11 |
2,5 |
5 |
9,50 |
45 |
9 |
0,12 |
4,9 |
6 |
9,40 |
37 |
23 |
0,10 |
2,6 |
7 |
11,60 |
58 |
15 |
0,13 |
4,6 |
8 |
8,14 |
27 |
17 |
0,09 |
3,4 |
9 |
15,62 |
58 |
28 |
0,07 |
4,8 |
10 |
11,12 |
47 |
16 |
0,12 |
4,9 |
11 |
7,34 |
38 |
7 |
0,08 |
3,2 |
12 |
10,58 |
44 |
15 |
0,11 |
4,7 |
13 |
7,37 |
23 |
25 |
0,15 |
2,7 |
14 |
10,63 |
57 |
8 |
0,13 |
5,0 |
15 |
10,63 |
38 |
24 |
0,07 |
2,9 |