1.4. Парабола

Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.

Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Пусть фокус имеет координаты 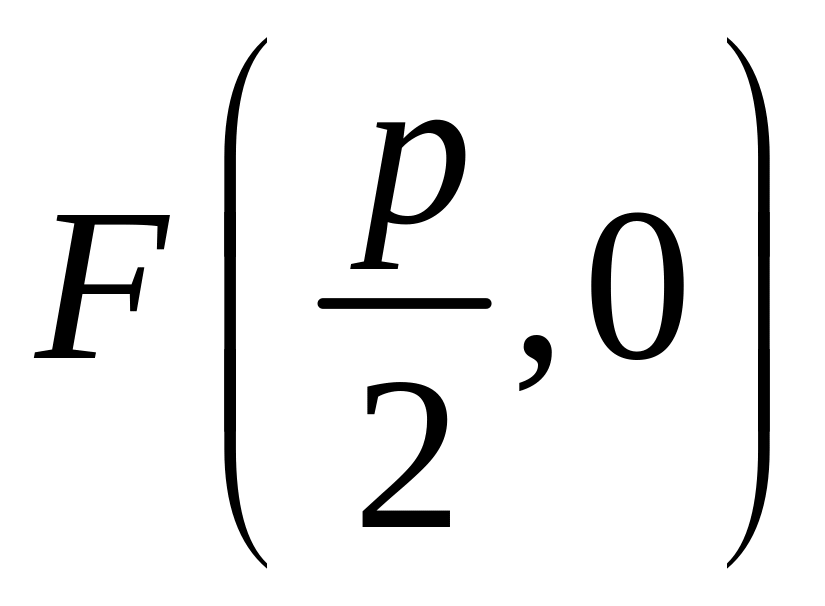, а уравнение директрисы имеет вид . Тогда уравнение параболы запишется в виде:

(9)

Данное уравнение называется каноническим уравнением параболы. Ось абсцисс будет являться осью симметрии параболы, заданной уравнением (9). При все точки такой параболы располагаются в правой полуплоскости (рис. 5), а при – в правой.

Рис. 5

Если же мы поместим фокус на оси ординат, т.е. он будет иметь координаты 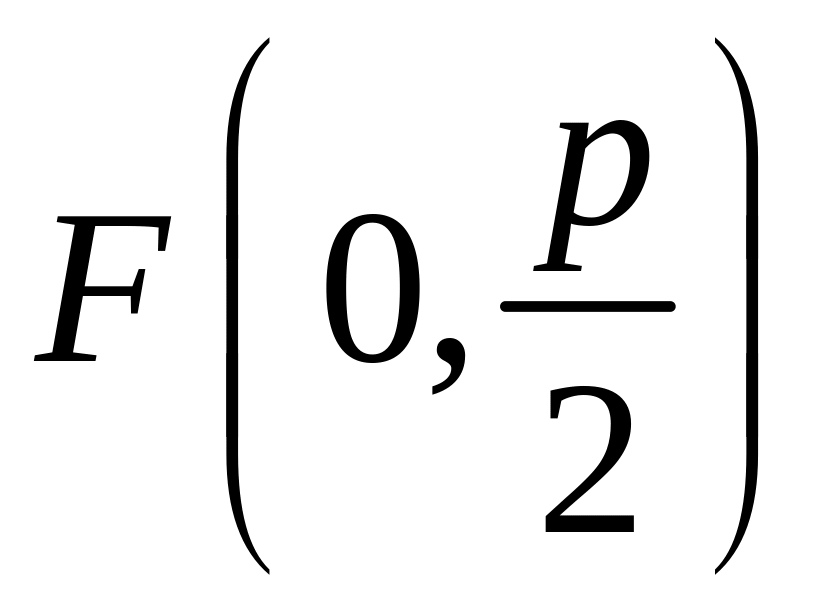, а уравнение директрисы имеет вид , то канонической уравнение параболы выглядит так:

(10)

Для параболы, заданной уравнением (10), осью симметрии является ось ординат. При все точки такой параболы располагаются в верхней полуплоскости, а при – в нижней.

Р ис. 6

2. Приведение уравнений кривых второго порядка к каноническому виду с помощью преобразования координат

2.1. Пятичленное уравнение кривой второго порядка

Вернемся к общему уравнению кривой второго порядка (1). Предположим для начала, что коэффициент уравнения B равен нулю, т.е. в уравнении отсутствует смешанное произведение x и y. Итак, уравнение является пятичленным:

,

(11)

Рассмотрим следующие случаи уравнения (11):

1. Пусть ; тогда уравнение определяет эллипс (действительный, мнимый или выродившийся в точку). Если , то получим окружность.

2. Пусть ; тогда мы имеем дело с гиперболой, вырожденный случай которой представляет собой пару пересекающихся прямых (если левая часть уравнения может быть представлена в виде произведения двух линейных сомножителей).

3. Пусть , но ; тогда уравнение описывает параболу, которая может вырождаться в пару пересекающихся прямых, если левая часть уравнения не содержит одной из двух переменных x или y.

Для установления вида кривой и ее расположения необходимо привести уравнение к каноническому виду, первоначально выделив полные квадраты по переменным и .

.

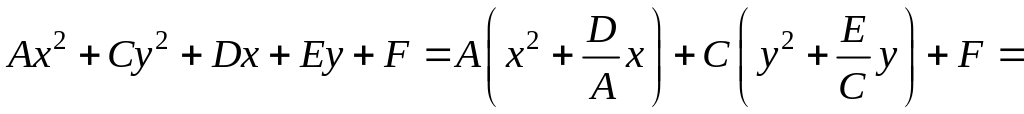
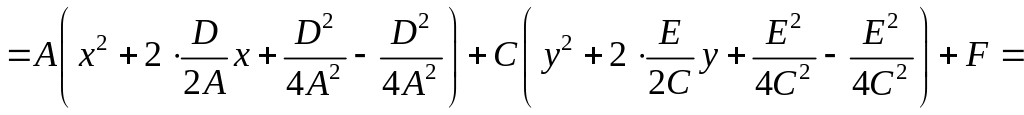
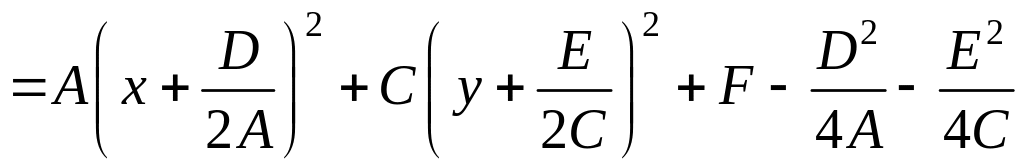Обозначим , , 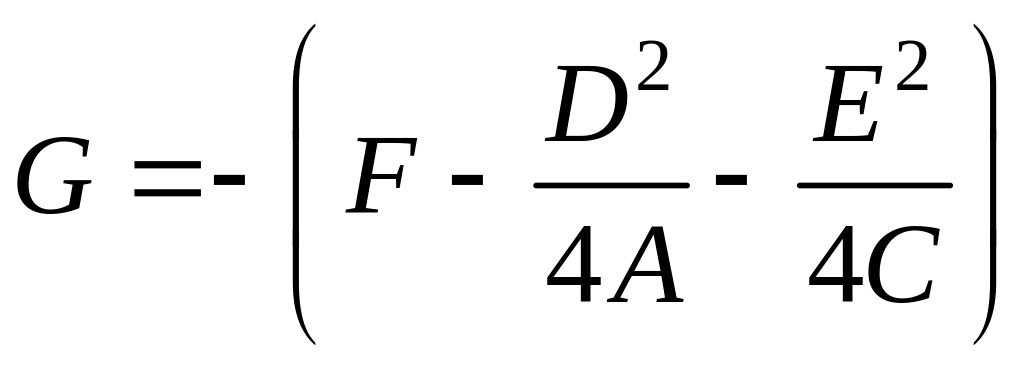. Получим

,

(12)

Остается только перенести в правую сторону равенства (12) и, разделив обе части на , получить каноническое уравнение кривой в новой декартовой системе координат, полученной из старой параллельным переносом начала координат в точку .

2.2. Полное уравнение кривой второго порядка

Теперь рассмотрим уравнение кривой второго порядка, в котором коэффициент .

В этом случае необходимо применить преобразование поворота осей координат по формулам:

(13)

При этом угол подбирается таким образом, чтобы уравнение стало пятичленным, т.е. не содержащим произведения . Дальнейшие преобразования аналогичны приведенным выше преобразованиям для пятичленного уравнения.