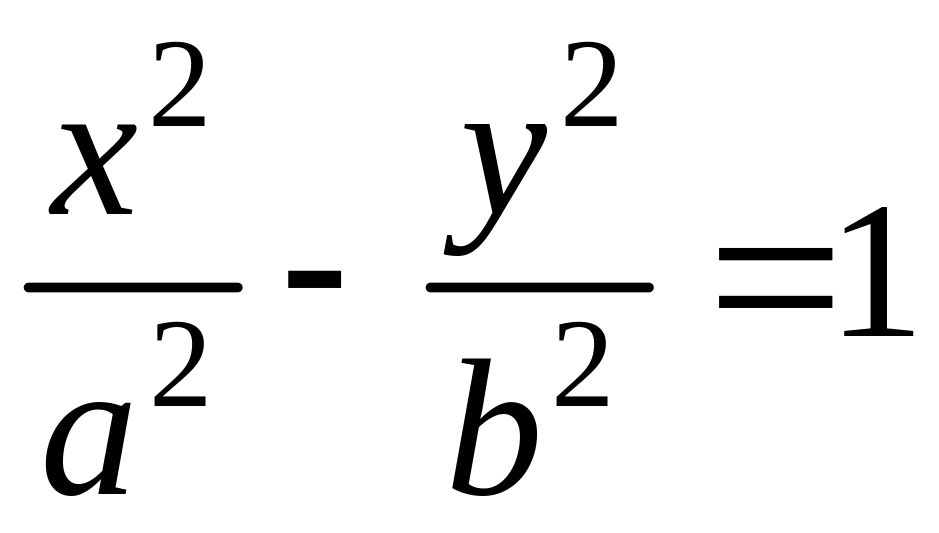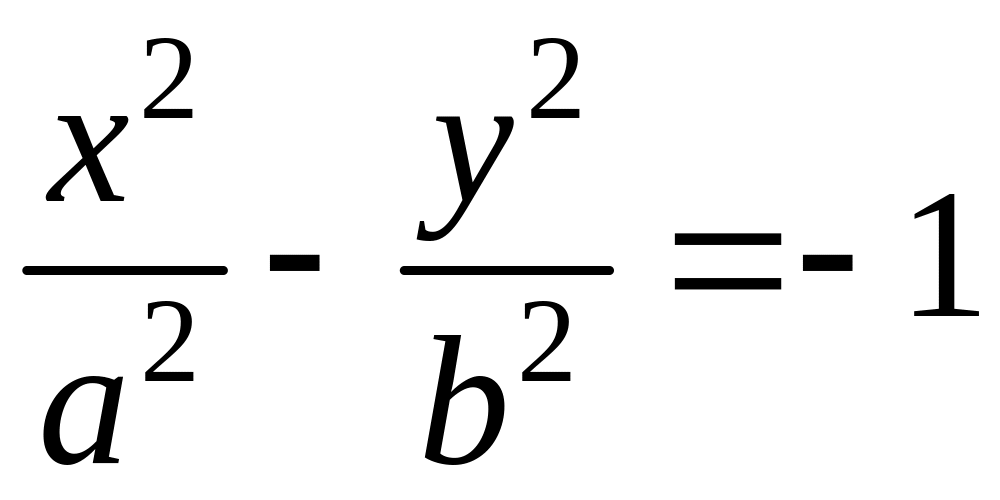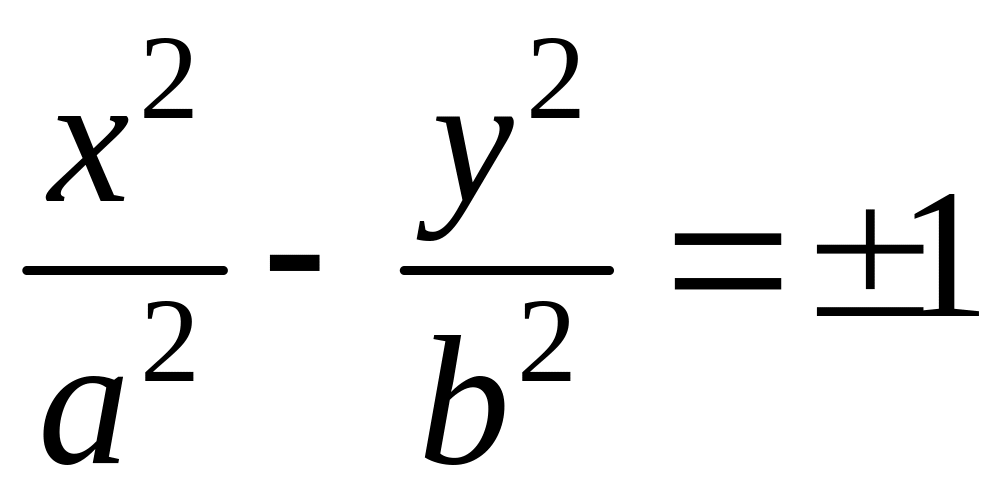О. В. ГАТЕЛЮК, А. М. СОКОЛЬНИКОВА

КРИВЫЕ ВТОРОГО ПОРЯДКА

ОМСК 20011

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

___________________________________

О. В. Гателюк, А. М. Сокольникова

КРИВЫЕ ВТОРОГО ПОРЯДКА

Утверждено редакционно-издательским советом университета

в качестве методических указаний для индивидуальной работы

студентов первого курса всех специальностей

Омск 2011

УДК 514.12(07)

ББК 22.151.54я7

С13

Кривые второго порядка: Методические указания для индивидуальной работы студентов первого курса / О. В. Гателюк, А. М. Сокольникова; Омский гос. ун-т путей сообщения. Омск, 2011. 27 с.

Методические указания написаны в соответствии с действующей программой по курсу математики для технических вузов, содержат основные виды кривых второго порядка. Приведены примеры решения стандартных задач, варианты типового расчета.

Предназначены для студентов первого курса очной и заочной форм обучения всех специальностей.

Библиогр.: 8 назв. Рис. 11.Табл. 6

Рецензенты:;

канд. пед. наук, доцент И. А. Круглова

_________________________

© Омский гос. университет

путей сообщения, 2011

ОГЛАВЛЕНИЕ

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1. Типы кривых второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.1. Основные понятия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2. Эллипс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.3. Гипербола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.4. Парабола. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2. Приведение уравнений кривых второго порядка к каноническому виду с помощью преобразования координат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.1. Пятичленное уравнение кривой второго порядка . . . . . . . . . . . . . . . . 2.2. Полное уравнение кривой второго порядка . . . . . . . . . . . . . . . . . . . . 3. Примеры выполнения заданий типового расчета. . . . . . . . . . . . . . . . . . . . 4. Варианты типового расчета «Кривые второго порядка» . . . . . . . . . . . . . . Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 6 6 6 8 10 11 11 12 13 18 25

ВВЕДЕНИЕ

Методические указания содержат краткие теоретические сведения по теме «Кривые второго порядка» из курса аналитической геометрии.

Цель данных указаний – помочь первокурсникам в изучении свойств и методов построения кривых второго порядка на плоскости. Для удобства пользования данными методическими указаниями приведены основные формулы и даны основные определения. Однако, большее внимание уделяется не выводу математических формул, а их практическому применению.

Часть методических указаний посвящена решению нескольких стандартных задач по данной теме. Задачи сопровождаются подробными объяснениями, которые должны помочь студенту при решении типового расчета.

Задания типового расчета подобраны таким образом, что их выполнение обеспечивает закрепление навыков решения стандартных задач: определение по виду уравнений вида кривой, приведение пяти- и шестичленного уравнения кривой к каноническому виду; построение кривой.

Задания соответствуют различным уровням сложности. Первые два имеют простой уровень и для их решения достаточно лишь усвоения начального теоретического материала. Решение третьего и четвертого задания требуют определенных практических навыков и могут быть отнесены ко второму уровню сложности. Пятое и шестое задания предназначены для студентов, полностью овладевших теорией по данному разделу и имеющих хороший практический опыт решения подобных задач.

Приведены примеры решения задач из предлагаемого студентам типового расчета.

1. Типы кривых второго порядка

1.1. Основные понятия

Кривой второго порядка называется линия, имеющая в некоторой декартовой системе координат уравнение второй степени относительно x и y

,

(1)

где .

Можно показать, что уравнение (1) может задавать только эллипс, параболу или гиперболу. Остальные случаи будем называть вырожденными. Ниже рассмотрим подробнее все перечисленные типы кривых второго порядка.

1.2. Эллипс

Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.

Обозначим фокусы эллипса через F₁ и F₂, расстояние между ними назовем фокусным расстоянием и обозначим 2c, а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокуса, через 2a (по условию ).

Введем декартову систему координат так, чтобы фокусы F1 и F2 оказались на оси абсцисс, а начало координат совпало с серединой отрезка F1F2. В выбранной таким образом системе координат левый фокус имеет координаты , а правый – (рис. 1)

Р ис. 1

Пусть – произвольная точка эллипса. По определению сумма расстояний от этой точки до фокусов равна 2a. Исходя из этого факта и введя обозначение , получим уравнение эллипса:

(2)

Оно называется каноническим уравнением эллипса. Здесь a и b – большая и малая полуоси эллипса. Оси координат будут являться также осями симметрии эллипса.

В описанном выше случае . Если фокусы F1 и F2 располагаются на оси ординат симметрично относительно начала координат, т.е. имеют координаты и , то обозначив сумму расстояний от любой точки эллипса до фокусов 2b и введя , вновь получим уравнение (2), но при этом (рис. 2) Точка называется центром, а точки с координатами и – вершинами эллипса.

Р ис. 2

Отношение величины расстояния между фокусами к длине большей оси называется эксцентриситетом эллипса и обозначается e.

(3а)

или

(3б)

Отсюда и возникло название кривой: в переводе с греческого эллипс означает «недостаток».

При построении эллипс вписывают в «опорный» прямоугольник, т.е прямоугольник с центром в начале координат и длинами сторон 2a и 2b.

В случае равенства осей уравнение принимает вид

(4)

и мы получаем частный случай эллипса – окружность. У окружности расстояние между фокусами равно нулю , оба фокуса при этом совпадают с центром окружности.

Обычно для построения эллипса на осях координат откладывают полуоси и строят прямоугольник со сторонами, параллельными осям координат. При этом длины сторон и , а серединами сторон являются точки и . Затем в полученный прямоугольник вписывают эллипс.

1.3. Гипербола

Гиперболой называется геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.

Введем декартову систему координат аналогично случаю, описанному выше для эллипса, т.е. фокусы имеют координаты и (рис. 3). Каноническое уравнение гиперболы в этом случае будет иметь вид:

(5)

Рис. 3

Здесь или . При этом a называется действительной, а b – мнимой полуосью гиперболы.

При гипербола называется равнобочной.

Если же декартова система координат выбрана таким образом, что фокусы имеют координаты и (рис.4), то каноническое уравнение гиперболы принимает вид:

(6)

В этом случае b называется действительно полуосью, а a – мнимой.

Объединив формулы (5) и (6), получим каноническое уравнение гиперболы в виде:

(7)

Р ис. 4

Как и в случае с эллипсом, координатные оси являются осями симметрии, а точка – центром симметрии гиперболы. Прямые обладают следующим свойством: точки гиперболы при удалении от начала координат (при ) подходят сколь угодно близко к этим прямым. Прямые с таким свойством называются асимптотами.

Точка называется центром гиперболы. Точки с координатами в случае, описанном уравнением (5), и точки с координатами в случае, описанном уравнением (6), называются вершинами гиперболы.

Отношение величины расстояния между фокусами к длине действительной полуоси называется эксцентриситетом гиперболы

(8а)

или

(8б)

Отсюда и возникло название кривой: в переводе с греческого гипербола означает «избыток».

Для построения гиперболы сначала строим опорный прямоугольник со сторонами длины и , параллельными осям координат, и серединами сторон и . Каждая из двух ветвей гиперболы вписана в бесконечную область, ограниченную продолжением диагоналей опорного прямоугольника и парой его сторон. Положение ветвей определяется знаком в правой части уравнения (7): если он отрицательный, то ветви вписаны в верхнюю и нижнюю область (вершины – точки ); если же положительный, то в правую и левую (соответственно вершинами являются точки ).