3.2.3. Вычисление определителя матрицы коэффициентов системы. Некоторые свойства определителей.

Поскольку преобразования прямого хода не меняют определителя матрицы системы, то его легко можно вычислить как произведение диагональных (ведущих) элементов полученной треугольной матрицы, т.е.

. (3.2.9)

Укажем ниже некоторые свойства определителя матрицы.

1. Если к элементам некоторой строки (или некоторого столбца) матрицы прибавить соответствующие элементы другой строки (другого столбца) матрицы, умноженные на произвольный множитель, то величина определителя не изменится.

2. Если к элементам некоторой строки матрицы прибавить соответствующие элементы строки, являющейся линейной комбинацией других строк матрицы (с какими угодно коэффициентами), то величина определителя не изменится.

3. При перестановке местами двух строк (или двух столбцов) матрицы определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.

4. Умножение всех элементов некоторой строки (или некоторого столбца) матрицы на одно и тоже число равносильно умножению определителя на это число.

5. При транспонировании матрицы величина определителя матрицы не меняется.

6. Определитель матрицы с двумя одинаковыми строками (или столбцами) равен нулю.

3.2.4. Выбор главного элемента.

Существует вероятность, что значение ведущего элемента в формулах (3.2.6) либо равно нулю, либо мало. Тогда число не может быть правильно вычислено. Например, если , то (бесконечность). Во избежание такой ситуации, а также для повышения общей точности вычислений, рекомендуется выбирать среди всех строк, начиная с k-ой, такую, в которой k-й элемент является наибольшим среди этих строк и затем переставить выбранную строку с k-ой строкой. Такой подход называется выбором главного элемента по столбцу и широко применяется на практике. Также возможен выбор главного элемента по строке, но это менее выгодно с вычислительной точки зрения. Для обеспечения наибольшей надежности вычислений во многих стандартных программах применяется выбор главного элемента по всей матрице, также сопряженный с аналогичной перестановкой столбцов, что соответствует изменению нумерации неизвестных. Данный вариант актуален, например, если матрица A имеет большое число обусловленности.

3.2.5. LU-разложение.

Итак, идея метода Гаусса состоит в преобразовании исходной системы (3.2.3) в эквивалентную систему с треугольной матрицей (треугольную систему). Последняя, как было показано выше, решается относительно «легко». Рассмотрим ниже прямой ход метода Гаусса на языке матричных разложений.

1-й шаг эквивалентен умножению исходной матрицы на матрицу

,

т.е. в результате матрица коэффициентов системы принимает вид:

.

2-й шаг эквивалентен умножению матрицы на матрицу

,

т.е. в результате матрица коэффициентов системы принимает вид:

.

k-й шаг эквивалентен умножению матрицы на матрицу

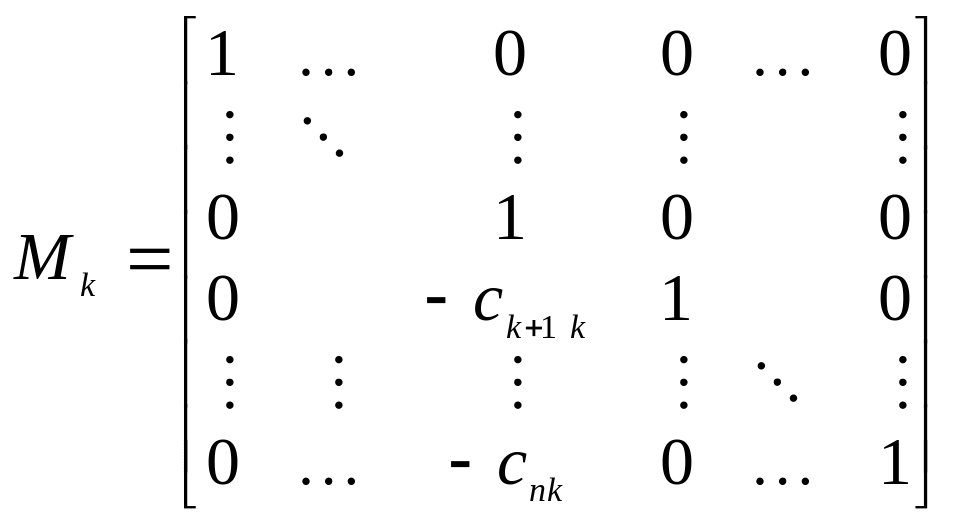, (3.2.10)

т.е. в результате матрица коэффициентов системы принимает вид:

.

Продолжая процесс, после шагов получим матрицу коэффициентов вида:

Заметим, что матрицы называются матрицами преобразования Гаусса.

Вводя переобозначение , получим:

. (3.2.11)

Как было показано выше (см. пункт 3.2.2), матрица является верхней треугольной.

Непосредственной проверкой несложно убедиться, что матрица, обратная к (3.2.10) определяется по формуле

. (3.2.12)

Таким образом, можно записать:

, (3.2.13)

где . (3.2.14)

Заметим, что каждая из матриц является нижней треугольной матрицей. Из линейной алгебры известно [18], что произведение нижних (верхних) треугольных матриц является нижней (верхней) треугольной матрицей. Тогда – нижняя треугольная матрица.

Разложение (3.2.13) называется LU-разложением матрицы .

В целом, можно сказать, что LU-разложение является «высоким уровнем» алгебраического описания метода Гаусса [11,18].

Решение исходной задачи (3.2.3) может быть найдено посредством последовательного решения двух треугольных систем:

,  . (3.2.15)

Анализируя описанный выше алгоритм, следует отметить очевидную

необходимость проверки главных элементов на равенство нулю, что свидетельствует о том, что LU-разложение может не существовать.

Для описания схем выбора главного элемента, рассмотренных в пункте 3.2.4, в «матричных терминах» необходимо ввести понятие матрицы перестановок. Матрица перестановок – это матрица, отличающаяся от единичной лишь перестановкой строк или, иначе, это матрица, у которой в любой ее строке и в любом ее столбце в точности один элемент равен 1, а остальные равны 0.

Заметим, что если – матрица перестановок, а – некоторая матрица, то тогда матрица является вариантом матрицы с переставленными столбцами, а матрица – вариантом матрицы с переставленными строками. Так, например, если – это, в частности, матрица, полученная из единичной перестановкой p-й и q-й строк, то матрица отличается от матрицы перестановкой p-й и q-й строк, а отличается от перстановкой p-го и q-го столбцов.

Матрицы перестановок ортогональны, т.е. если – матрица перестановок, то . Произведение матриц перестановок также является матрицей перестановок.

Итак, при использовании рассмотренных ранее схем выбора главного элемента в общем случае получается LU-разложение для матрицы вида

, (3.2.16)

где и – матрицы перестановок.

Разложение (3.2.16) справедливо для произвольной матрицы.

Решение системы (3.2.3) в этом случае также находится достаточно просто путем решения двух треугольных систем:

, (3.2.17)

и последующим переходом

. (3.2.18)

Важным частным случаем разложения (3.2.16) является разложение

, (3.2.19)

где – матрица перестановок.

Это разложение, возникающее в частности, при использовании схемы выбора главного элемента по столбцу, выполнимо для любой невырожденной матрицы.