3.1.4. Скалярное произведение векторов.

Несложно показать, что арифметическое пространство является евклидовым пространством.

Скалярное произведение векторов и обозначается как

, (3.1.30)

т.е. двум векторам и ставится в соответствие число s (скобки – это стандартное обозначение скалярного произведения).

В соответствии с данным выше определением евклидового пространства скалярное произведение векторов должно обладать свойствами:

; ; ;

, если и , если . (3.1.31)

Чаще всего скалярное произведение векторов определяется формулой

. (3.1.32)

Можно показать, что оно удовлетворяет всем указанным выше свойствам.

В частности, евклидовым пространством является пространство векторов, рассматриваемых в курсе аналитической геометрии.

Положительно определенной матрицей называется вещественная сим-

метричная матрица, если для любого вектора пространства справедливы соотношения:

, если и , если . (3.1.33)

Заметим, что определенная выше операция скалярного произведения векторов является наиболее употребляемой. Вместе с тем, существует более общая формула определения скалярного произведения векторов

, (3.1.34)

где – положительно определенная симметричная матрица. В выше приведенном случае (формула (3.1.32)) .

Можно показать, что для любой матрицы A справедливо равенство

. (3.1.35)

3.1.5. Норма вектора. Некоторые свойства векторных норм. Абсолютная и относительная погрешности. Сходимость.

Некоторым обобщением понятия длины вектора (оценкой величины вектора) является величина, называемая норма вектора. Функция

является нормой вектора, если она обладает следующими свойствами:

1) 0 (равенство только при );

2) ;

3) – неравенство треугольника.

Чтобы отличить одну норму от другой используются индексы при двойной черте.

Полезный класс векторных норм – это p-нормы, определяемые как

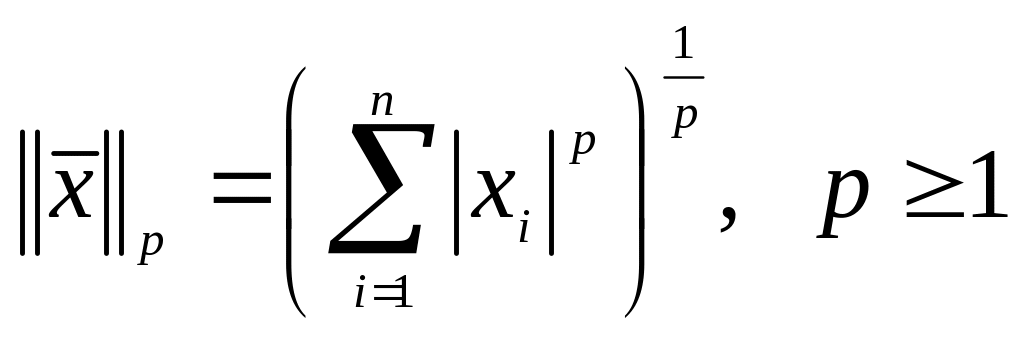. (3.1.36)

Наиболее важными из p-норм являются 1, 2 и нормы:

(3.1.37)

– норма по модулю (частный случай (3.1.36) при );

(3.1.38)

– «евклидова» норма (частный случай (3.1.36) при );

(3.1.39)

– максимум модуля для элементов вектора (частный случай (3.1.36) при ).

Очевидно, что евклидова норма . Это соответствует естественному понятию длины вектора в двумерном и трехмерном пространстве.

Единичным вектором по отношению к норме называется вектор , удовлетворяющий равенству .

Классический результат о p-нормах – неравенство Гельдера

. (3.1.40)

Очень важным частным случаем этого неравенства является неравенство Коши-Шварца:

. (3.1.41)

Все нормы в эквивалентны, т.е. для двух норм и в существуют положительные константы и , такие, что

(3.1.42)

для всех из пространства . Например, для вектора из имеем:

; ; . (3.1.43)

В вычислительной математике большую роль играет понятие «близости» двух векторов. Это соответствует понятию «расстояния», определяемому формулой

, (3.1.44)

т.е. расстояние между векторами равно норме от их разности:

, где . (3.1.45)

Оценка близости двух векторов используется для определения погрешности решения в итерационных методах.

Пусть вектор пространства есть аппроксимация к вектору пространства . Для заданной векторной нормы будем говорить, что

(3.1.46)

есть абсолютная погрешность , а при формула

(3.1.47)

задает относительную погрешность .

Сходимость. Будем говорить, что последовательность векторов , , …, , … сходится к вектору , если

. (3.1.48)

Отметим, что вследствие приведенных выше свойств векторных норм сходимость в -норме влечет сходимость в -норме и наоборот.