3.6.2. Решение систем нелинейных уравнений.

Общий вид системы уравнений с неизвестными

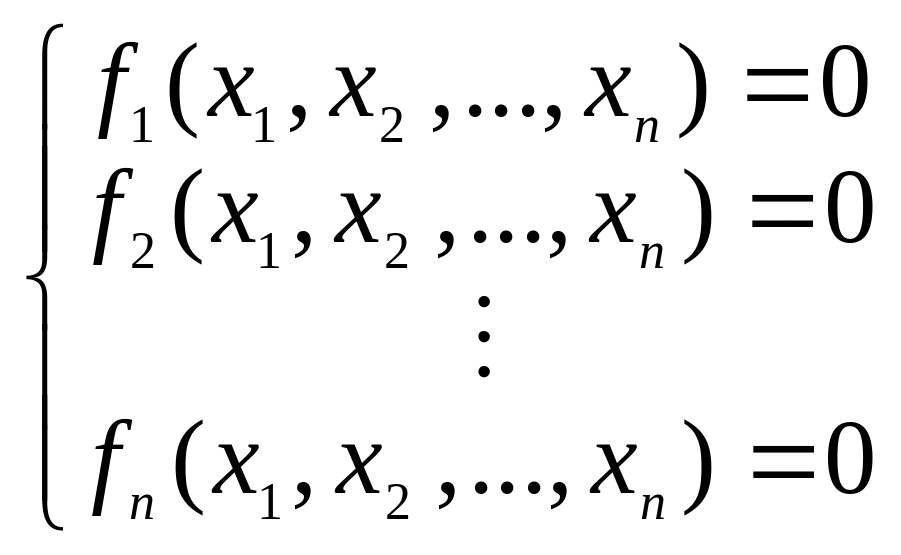(3.6.31)

или , (3.6.32)

; . (3.6.33)

Метод простой итерации. Представим систему (3.6.32) в виде

, где 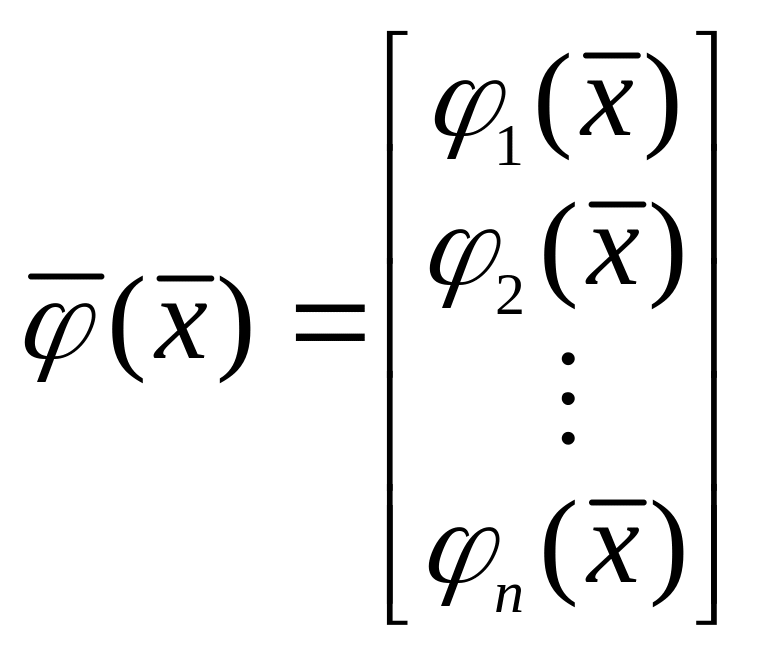. (3.6.34)

Например: если , то . (3.6.35)

Алгоритм пересчета по методу простой итерации имеет вид

, ; – задается. (3.6.36)

Процесс заканчивается если

. (3.6.37)

Рассмотрим сходимость метода простой итерации. Из формулы Тейлора вытекает следующая зависимость

, (3.6.38)

где – точное решение; – «промежуточное значение» между и ;

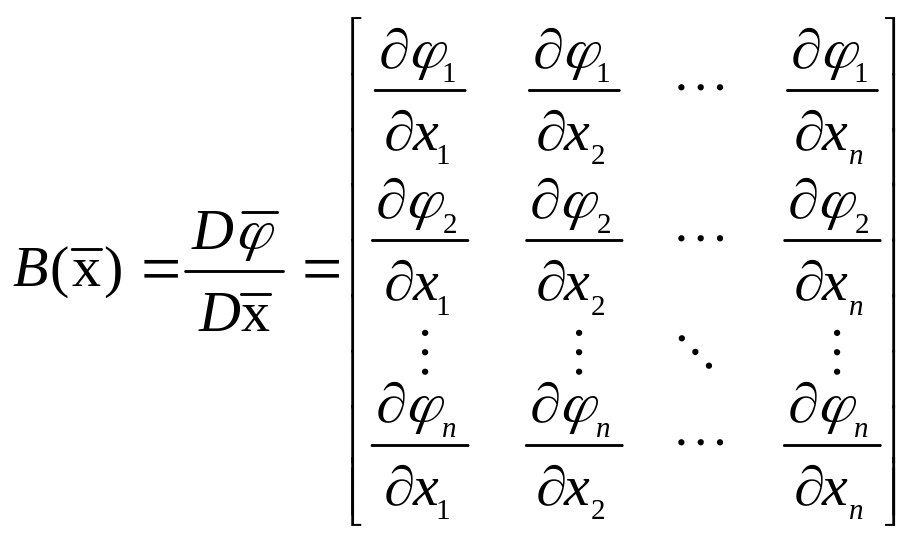– матрица Якоби; (3.6.39)

Таким образом, (3.6.40)

Для уменьшения погрешности, т.е. для сходимости, достаточно, чтобы норма матрицы Якоби была меньше единицы. Обозначим

. (3.6.41)

Тогда для сходимости достаточно выполнения любого из трех условий:

для всех ; (3.6.42)

для всех ; (3.6.43)

относительно всех и ; . (3.6.44)

Метод Ньютона. Метод Ньютона для системы (3.6.32) имеет вид:

, (3.6.45)

где является значением матрицы Якоби при :

. (3.6.46)

Окончанием итерационного процесса может быть выполнение одного из следующих условий:

– оценка невязки

; (3.6.47)

– оценка погрешности

. (3.6.48)

На практике можно перевычислять не для каждого шага итерации , а, например, для , или даже с еще более крупным шагом по .

Пример 3.6.1. Решить систему нелинейных уравнений

, где ; .

Итерационный процесс по методу Ньютона:

,

Для данного примера матрица Якоби имеет вид:

,

откуда

и формула пересчета примет вид:

при начальном приближении: , .

Нулевой шаг:

.

Первый шаг:

Проверка (оценка невязки):

; ■.

§ 3.7. Метод наименьших квадратов

3.7.1. Понятие о методе наименьших квадратов (мнк).

Пусть имеются результаты некоторой серии экспериментов, в которой выявлено, например, попарное соответствие некоторых параметров и (см. таблицу 3.7.1, где – номер опыта; , – результаты эксперимента).

Таблица 3.7.1. Результаты серии экспериментов.

			…		…
			…		…

В таких случаях, как правило, целью эксперимента является выявление зависимости между величинами и . Например, если экспериментальные точки на плоскости располагаются достаточно близко от некоторой кривой, то целесообразно получить аналитический вид этой кривой в виде .

Чаще всего такая задача решается при условии, что задан (из каких-либо практических соображений) общий вид этой кривой (полином, экспонента, сумма синусоид или др.). Такая кривая, как правило, зависит от нескольких параметров. Определением этих параметров можно получить оптимальное (наилучшее) приближение искомой зависимости в классе заданного вида кривых.

Наиболее простым случаем является представление искомой зависимости в виде полинома, т.е. требуется найти полином вида

, (3.7.1)

заданной степени , наилучшим образом отображающий полученную в эксперименте зависимость от .

Введем обозначения

, (3.7.2)

– отклонения величин значений кривой и точек эксперимента по координате (рис. 3.7.1), соответствующих одному и тому же значению .

Конечно оптимальной кривой будет такая, для которой эти отклонения будут минимальны. В соответствии с идеей метода, в качестве критерия минимума принимается минимум суммы квадратов отклонений по всем точкам эксперимента.

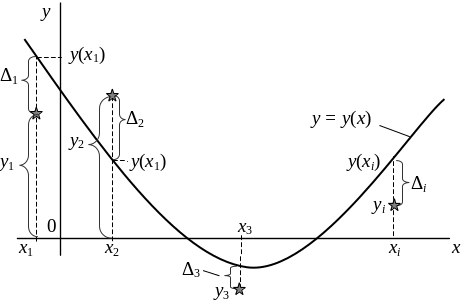
Рис. 3.7.1. Приближение результатов эксперимента некоторой кривой.

(3.7.3)

или с учетом (3.7.1)-(3.7.2)

. (3.7.4)

Таким образом, задача сводится к определению минимума , где уже является функцией от переменных, т.е.

. (3.7.5)

Из дифференциального исчисления известно, что условие минимума состоит в выполнении системы равенств

, . (3.7.6)

Распишем эти равенства, исходя из вида , получим:

, .

Следовательно, для определения коэффициентов оптимального полинома степени требуется решить систему линейных уравнений -го порядка:

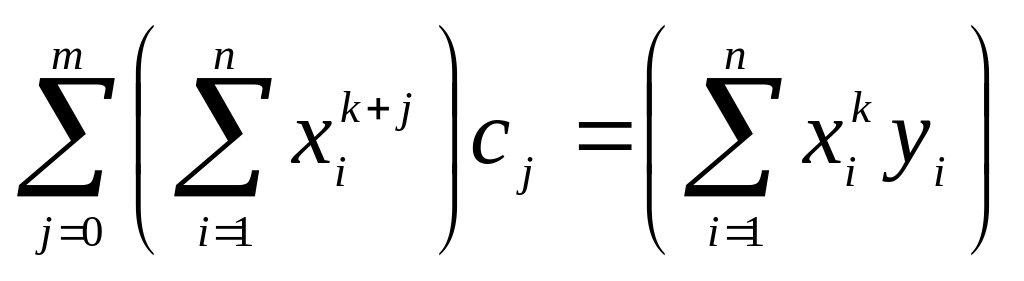, . (3.7.7)

Уравнения (3.7.7) называются нормальными уравнениями.

В частности, при для получения коэффициентов оптимальной квадратичной параболы требуется решить систему линейных уравнений третьего порядка

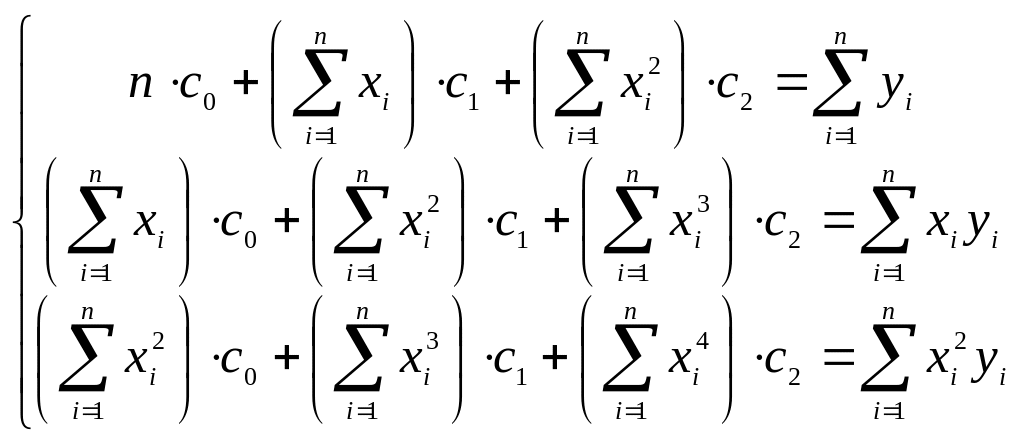(3.7.8)

Рассмотрим случай построения оптимальной прямой (полином в случае ) (рис. 3.7.2).

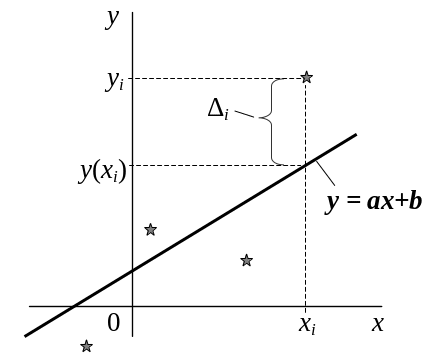
Рис. 3.7.2. Построение оптимальной прямой.

Параметры прямой и определяются из системы уравнений:

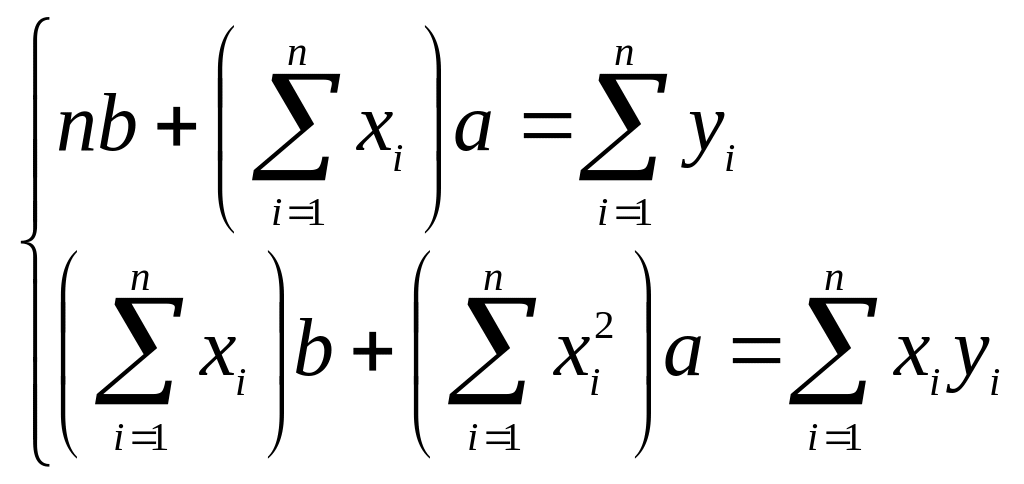(3.7.9)

или, записанной в более привычном виде (в системе (3.7.9) поменяли местами уравнения и неизвестные):

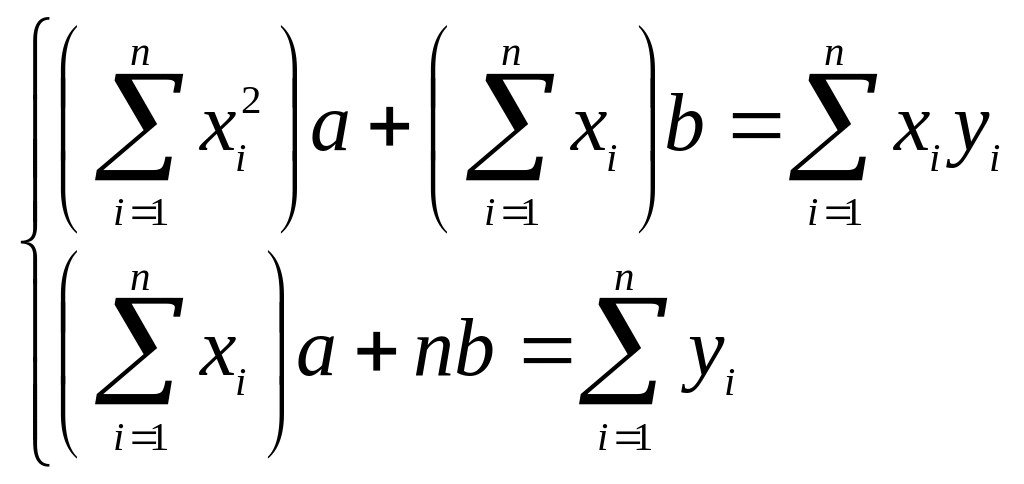(3.7.10)