3.5.2. Формула прямоугольников (формула средних).

Заменим на i-ом участке интегрируемую функцию постоянной величиной, например, равной ее значению в средней точке (рис. 3.5.2):

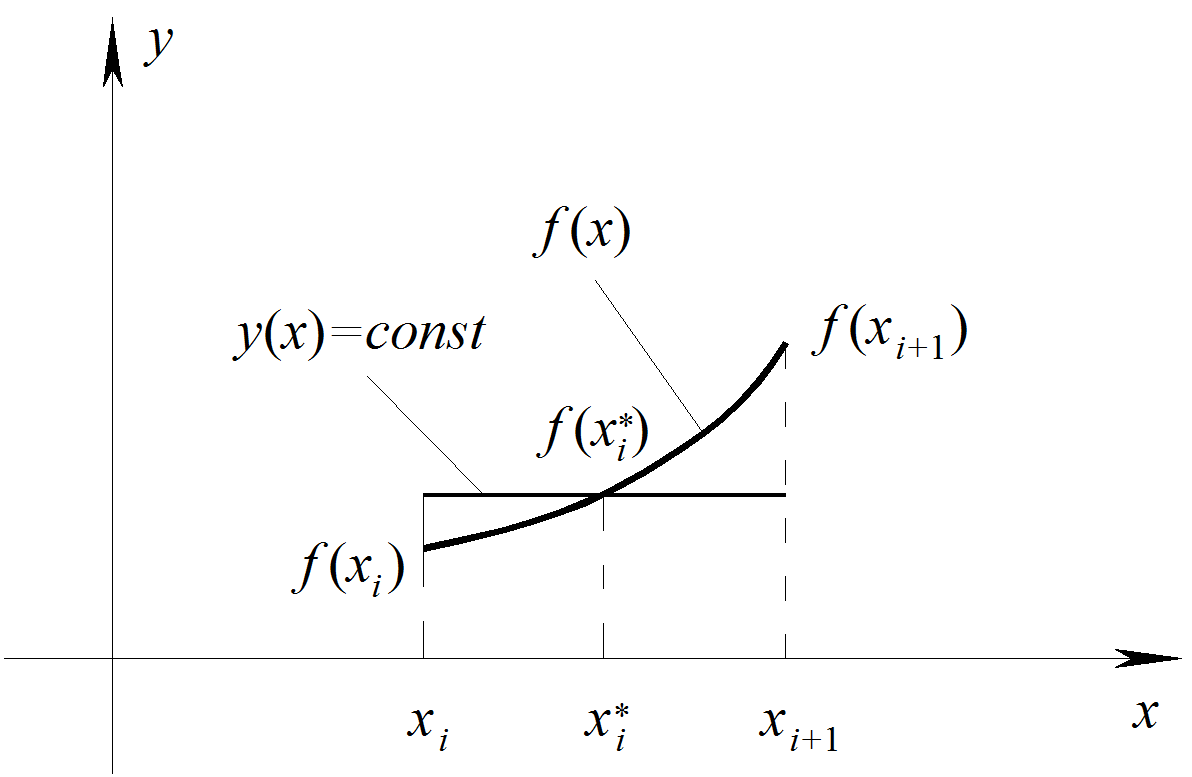
Рис. 3.5.2. К интегрированию по формуле прямоугольников.

, где . (3.5.4)

Тогда интеграл на отрезке заменяется площадью прямоугольника, т.е.

, (3.5.5)

и вычисление исходного интеграла сводится к вычислению суммы

. (3.5.6)

Заметим, что часто из практических соображений в качестве в формуле (3.5.6) берется , либо . В результате получаем:

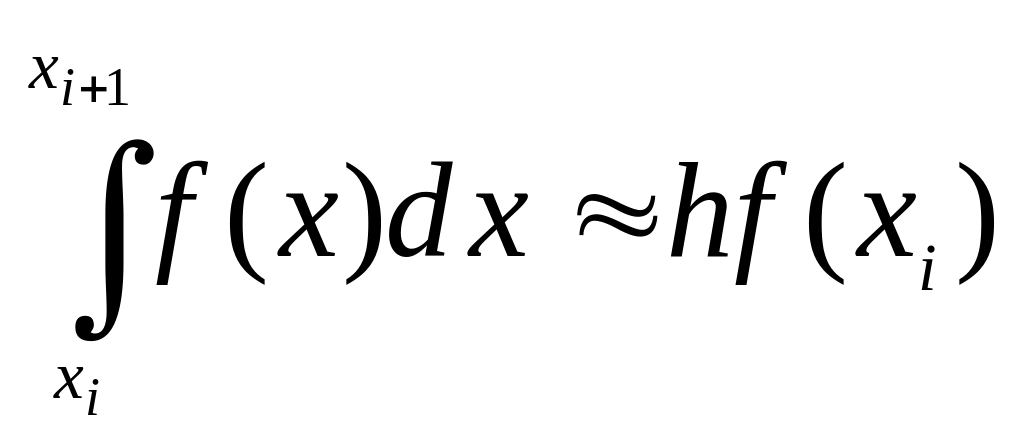(3.5.7)

– квадратурная формула «левых» прямоугольников;

(3.5.8)

– квадратурная формула «правых» прямоугольников.

Формулы (3.5.7) и (3.5.8) менее точные, чем (3.5.6), но иногда более удобные, например, при численном решении дифференциальных уравнений.

Точность вычисления. Как следует из построения квадратурные формулы прямоугольников дают точный результат интегрирования для функций, постоянных на i-ом участке ( ). Квадратурная формула «средних» прямоугольников дает точный результат также и для линейных на i-ом отрезке функций. Это утверждение достаточно проверить для .

При точном интегрировании получаем:

;

а при интегрировании по формуле «средних» прямоугольников

Как видно, результаты точного и численного интегрирования совпадают.

3.5.3. Формула трапеций.

Заменяем на i-ом участке интегрируемую функцию линейной функцией , принимающей в точках и значения (рис. 3.5.3):

, . (3.5.9)

Рис. 3.5.3. К интегрированию по формуле трапеций.

Тогда интеграл на отрезке заменятся площадью трапеции ( и – основания, – высота)

. (3.5.10)

Вычисление исходного интеграла сводится к вычислению суммы

, (3.5.11)

или . (3.5.12)

Точность вычисления. Как следует из построения квадратурная формула трапеций дает точный результат интегрирования для функций, линейных на i-ом участке ( ).

3.5.4. Формула Симпсона.

Разобьем интервал интегрирования на четное число отрезков. Рассмотрим сдвоенный участок [ ]. Построим параболу , принимающую в точках значения (рис. 3.5.4). Такая парабола может быть представлена формулой

, (3.5.13)

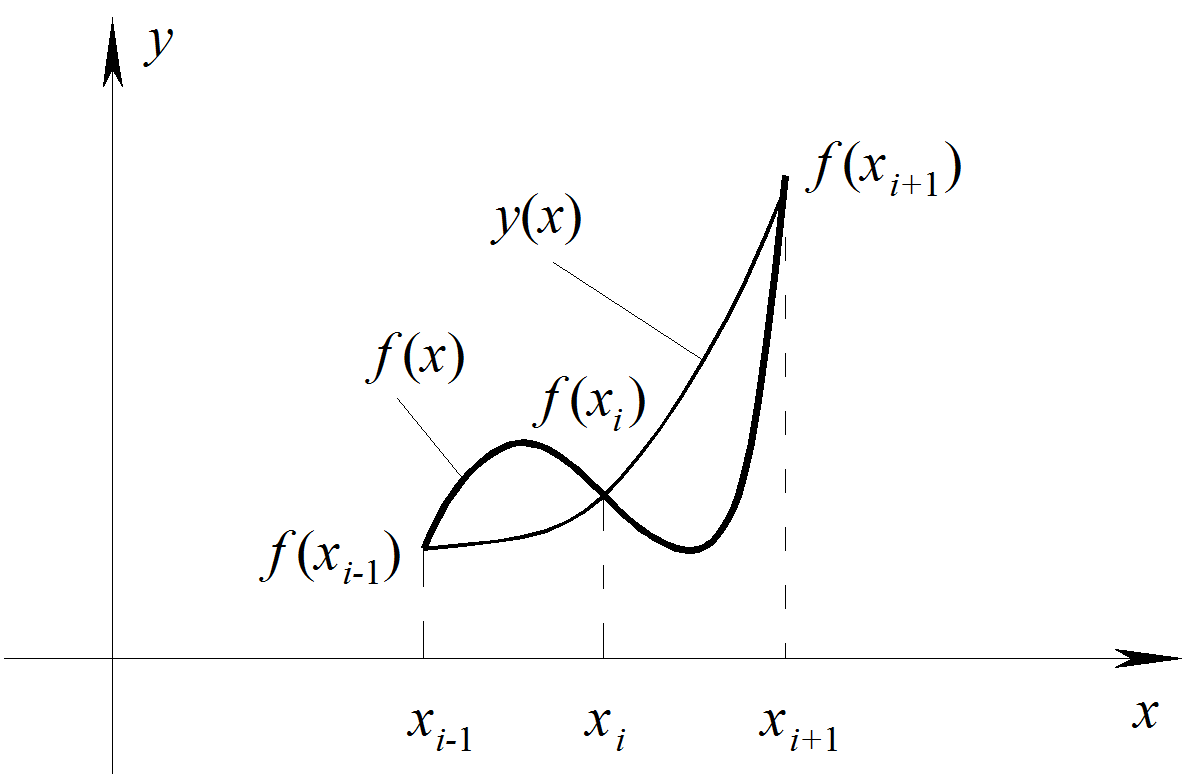
Рис. 3.5.4. К интегрированию по формуле Симпсона.

где , при этом (3.5.14)

или . (3.5.15)

Делая замену переменных, вычислим приближенное значение интеграла

.

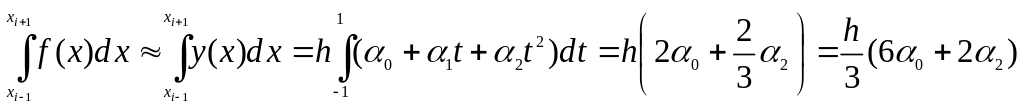Параметры , определим из условий

В итоге получим квадратурную формулу Симпсона

. (3.5.16)

Общая формула для вычисления приближенного значения интеграла примет вид

. (3.5.17)

Суммирование ведется только по нечетным i. Если перегруппировать члены суммы, получим

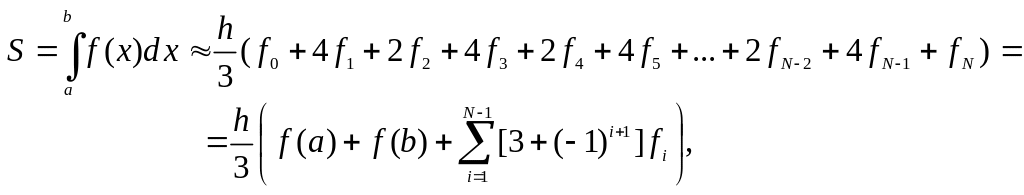
т.е. (3.5.18)

Точность вычисления. Как следует из построения квадратурные формулы Симпсона дают точный результат интегрирования для функций, имеющих вид квадратичной параболы на сдвоенном участке [ ] ( – нечетное). Заметим, что одинаковая длина сдвоенных участков вовсе не обязательна и использовалась здесь исключительно для упрощения промежуточных выкладок и вида результирующих формул (3.5.17)–(3.5.18). В том случае, когда сдвоенные участки имеют одинаковую длину ( – средняя точка сдвоенного участка), формула Симпсона точна для функций, имеющих вид кубической параболы на этих участках. Это утверждение достаточно проверить для .

При точном интегрировании имеем:

,

а при интегрирование по формуле Симпсона получаем:

=

Как видно, результаты точного и численного интегрирования совпадают.