3.4.5. Собственные значения обратной матрицы.

Пусть

,

т.е. и – собственное значение и собственный вектор матрицы A.

Умножая обе части данного равенства на , получим

.

Следовательно, – собственный вектор матрицы , а – собственное значение матрицы .

3.4.6. Обобщенная проблема собственных значений.

Пусть даны матрицы и , при этом – невырожденная. Требуется найти ненулевой вектор и число , удовлетворяющие равенству

. (3.4.23)

В этом случае и , соответственно, называются обобщенными собственным числом и собственным вектором.

Умножая на обе части (3.4.23), получим

. (3.4.24)

Таким образом, задачу можно свести к определению собственных чисел и векторов матрицы .

На практике в современных стандартных программных комплексах реализована непосредственно обобщенная проблема собственных значений. Для этих целей, например, используется так называемый QZ-алгоритм, представляющий собой устойчивое обобщение QR-алгоритма.

3.4.7. Вычисление минимального собственного числа степенным методом.

Как уже отмечалось в п. 3.4.5. собственные векторы матриц и

совпадают, а собственные значения связаны соотношением

, (3.4.25)

откуда , (3.4.26)

где – минимальное собственное значение матрицы ; – максимальное собственное значение матрицы .

Таким образом, для определения минимального собственного числа матрицы достаточно вычислить максимальное собственное число матрицы степенным методом.

§ 3.5. Методы численного интегрирования

3.5.1. Понятие о формулах численного интегрирования.

Пусть требуется вычислить определенный интеграл вида

. (3.5.1)

Для многих функций первообразные представляют собой достаточно сложные комбинации элементарных функций, либо вовсе не выражаются через них. В таких случаях использование формулы Ньютона-Лейбница на практике не представляется возможным. Во многих практических случаях достаточно получить значение интеграла с заданной точностью . Для вычисления приближенного значения интеграла существуют формулы численного интегрирования. Суть построения формул численного интегрирования состоит в следующем.

Разобьем отрезок на частей. Для простоты изложения положим эти части одинаковой длины .

Пронумеруем точки разбиения так, как показано на рис. 3.5.1. Имеем:

,

при этом .

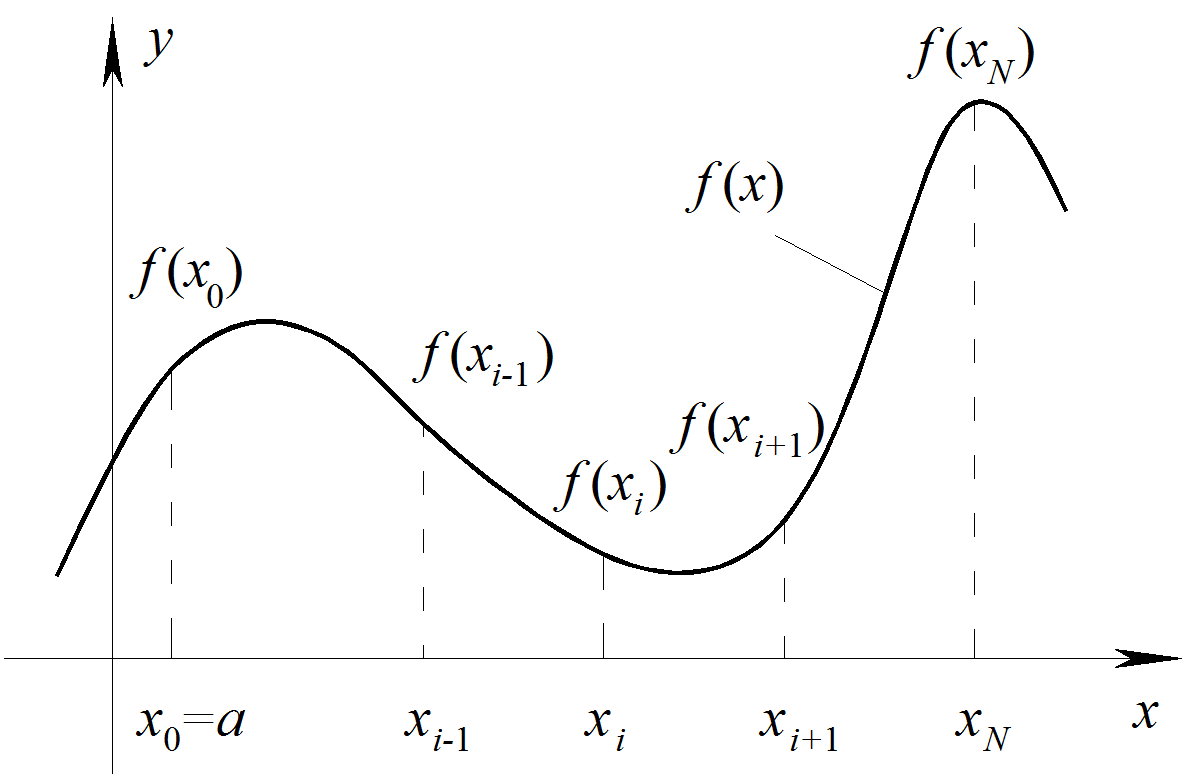
Рис. 3.5.1. К вопросу о численном интегрировании.

Исходный интеграл (3.5.1) может быть представлен в виде суммы интегралов по полученным в результате разбиения «малым» отрезкам:

. (3.5.2)

Интегралы

(3.5.3)

вычисляются по приближенным формулам.

Простейшие формулы для приближенного вычисления интегралов по отрезку называются квадратурными формулами [8,66]. Рассмотрим некоторые из них ниже, а также изучим вопросы их точности. Порядок точности квадратурной формулы определяется степенью полинома (многочлена), для которой эта квадратурная формула точна.