8.2. Построение аксонометрических проекций моделей

Наглядность изображения геометрического тела зависит от вида аксонометрической проекции и его ориентации относительно осей координат. Поэтому перед построением аксонометрической проекции модели на чертеже обозначают оси присоединенной к нему системы координат.

Последовательность построения аксонометрической проекции определяется формой модели. Построение аксонометрических проекций необходимо выполнять с использованием рациональных приемов построения, чтобы избежать лишней работы. Изображение начинают строить с основания и характерной части предмета, а затем последовательно пополняют его недостающими элементами.

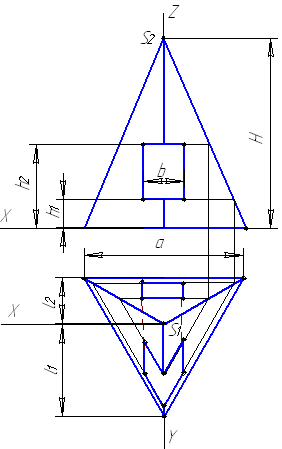
Пример 8.1. Построить аксонометрической проекции правильной пирамиды с поперечным сквозным отверстием (рис. 8.5 а - г).

1.На чертеже пирамиды обозначаем систему координат и отмечаем размеры, необходимые для построения аксонометрической проекции (рис. 8.5 а).

Выполняем построение целой пирамиды в изометрической и диметрической проекциях, чтобы определить, на которой из них получается наиболее наглядное изображение пирамиды.

2. Построение изометрической проекции (рис. 8.5 б). На оси Y в положительном и отрицательном направлениях отрезки соответственно L₁ и L₂ и получаем точки 1 и 2. Через точку 2 проводим прямую, параллельную оси X, и на ней откладываем в обе стороны отрезки, равные а/2. Концы этих отрезков – точки 3 и 4 соединяем прямыми с точкой 1 и получаем проекцию основания пирамиды.

На оси Z откладываем высоту пирамиды Н и получаем проекцию вершины S.

Строим боковые ребра пирамиды S – 1, S – 2 и S – 3.

3. Диметрическую проекцию пирамиды (рис. 8.5 в) строим в такой же последовательности, но отрезки L₁ и L₂, которые откладываем на оси Y, уменьшаем в два раза.

При сравнении построенных аксонометрических проекций пирамиды более наглядной оказалась диметрическая проекция, т. к. на ней видны обе передние грани.

При сравнении построенных аксонометрических проекций пирамиды более наглядной оказалась диметрическая проекция, т. к. на ней видны обе передние грани.

4. Диметрическую проекцию сквозного отверстия (рис. 8.5 г) начинаем с построения на высоте h₁ и h₂ двух треугольников, подобных основанию пирамиды. На каждом треугольнике на стороне, параллельной оси X, откладываем ширину отверстия b и получаем точки 1 и 2. Через эти точки проводим прямые, параллельные оси Y, и продолжаем их до пересечения со сторонами построенных треугольников. Соединяем прямыми линиями полученные отрезки верхнего и нижнего отсеков отверстия, принадлежащие одной боковой грани пирамиды.

5. Обводим видимые линии контура диметрической проекции.

б а

в г

Рис. 8.5

На аксонометрической проекции модели с отверстием с помощью двух секущих плоскостей удаляют часть предмета, чтобы показать его внутренние поверхности. Направление линий штриховки на плоскостях показано на рис. 8.6 а для изометрической проекции и на рис 8.5 б для диметрической проекции.

а б

Рис. 8.6

Задача 8.1. Построить изометрическую проекцию восьмиугольной призмы.	Задача 8.2. Построить фронтальную диметрию детали .
Задача 8.3. Построить профильную и прямоугольную диметрическую проекции модели. В аксонометрии применить вырез четверти.	Задача 8.4. Построить профильную и изометрическую проекции геометрического тела со сквозным отверстием. В аксонометрии применить вырез четверти.
Задача 8.5, 8.6. Построить комплексный чертеж по заданному аксонометрическому изображению детали.