7.3. Пересечение поверхностей вращения. Способ концентрических сфер

В некоторых случаях построения линии пересечения поверхностей целесообразно применять способ вспомогательных секущих сфер.

Способ концентрических сфер применяется при построении линии пересечения поверхностей вращения, если их оси в пространстве пересекаются и параллельны одной из плоскостей проекции.

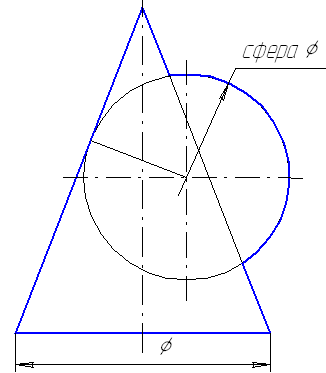
В основу способа положена следующая теорема. Две соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей (рис. 7.5).

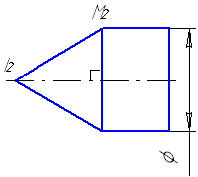
Рис. 7.5 Рис. 7.6

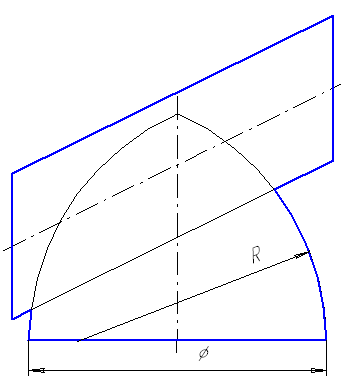
Если центр сферы расположен на оси поверхности вращения, то сфера пересекает данную поверхность по окружностям, которые проецируются на плоскость, параллельную оси, в прямые, перпендикулярные оси поверхности вращения (рис. 7.6).

Пример 7.5. Построить фронтальную проекцию линии пересечения двух конусов, оси которых пересекаются (рис. 7.7).

Высшая и низшая точки 1 и 2 линии пересечения определяются как точки пересечения очерков обоих конусов, т.к. плоскость, проведенная через оси конусов, является фронтальной плоскостью уровня.

Точки 3, 4 и 5 находим с помощью двух вспомогательных концентрических сфер.

Ц

Рис. 7.7

ентр сфер находится в точке О пересечения осей конусов. Точку 3 получаем с помощью сферы минимального радиуса R min. Она касается вертикального конуса по окружности m и пересекает наклонный конус по окружности n.

В пересечении фронтальных проекций m₂ и n₂ окружностей получена точка 3₂. Точки 4 получаем аналогично с помощью сферы большего радиуса.

Соединяем полученные точки.

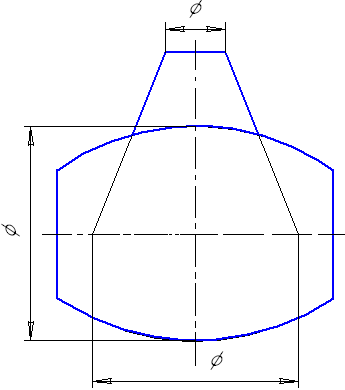
Если пересекаются два цилиндра одинакового диаметра с пересекающимися осями, то поверхности этих цилиндров описаны вокруг шара, диаметр которого равен диаметру цилиндров (рис. 7.8). Поверхности этих цилиндров пересекаются по эллипсам. Если оси цилиндров параллельны плоскости проекций, то эллипсы проецируются в прямые линии.

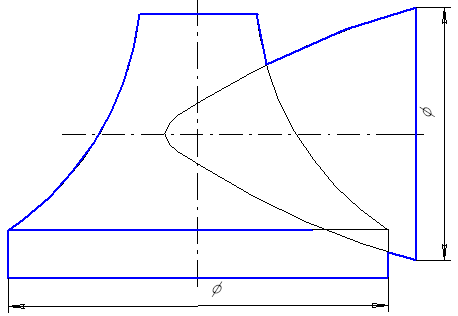
То же будет при построении линий пересечения поверхностей цилиндра и конуса или поверхностей конусов, если в них можно вписать общую сферу (рис. 7. 9).

Рис. 7.8 Рис. 7.9

Задача 7.14. Построить линию пересечения двух цилиндров.	Задача 7.15. Построить линию пересечения конуса со сферой.
Задача 7.16. Построить линию пересечения тора с конусом	Задача 7.17. Построить линию пересечения двух конусов
Задача 7.18. Построить линию пересечения данных поверхностей	Задача 7.19. Построить линию пересечения тора с наклонным цилиндром