6.4. Развертки поверхностей вращения

Процесс совмещения поверхности с плоскостью называется развертыванием поверхности. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертываемой, а полученная при этом плоская фигура – ее развертка.

К развертываемым поверхностям относятся только линейчатые поверхности, образующей которых является прямая. Из поверхностей вращения к таким относятся цилиндр и конус. Что касается поверхностей сферы и тора, то здесь можно говорить только об их условном развертывании.

Построение развертки цилиндра и конуса осуществляется в одинаковой последовательности. Сначала раскатывают боковую поверхность, а затем достраивают основание.

Развертку боковой поверхности прямого кругового цилиндра заменяют разверткой боковой поверхности правильной n-угольной призмы, вписанной в данный цилиндр. Развертку боковой поверхности прямого кругового конуса заменяют разверткой боковой поверхности правильной n-угольной пирамиды, вписанной в данные конус. Развертки получается приближенными, но эти искажения считаются допустимыми в начертательной геометрии.

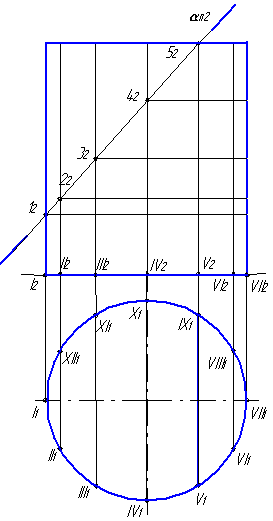
Пример 6.5. Построить развертку боковой поверхности прямого кругового цилиндра, усеченного плоскостью α (рис. 6.9 а,б).

1. Делим основание цилиндра на 12 равных частей и проводим через точки деления образующие цилиндра (рис. 6.9).

2. На фронтальной проекции отмечаем точки пересечения сечения цилиндра фронтально-проецирующей плоскостью α с образующими – точки 1₂, 2₂, 3₂, 4₂, 5₂. Достраиваем горизонтальную проекцию. Проводим линию пересечения заданной плоскости α с поверхностью цилиндра.

3

. На свободном поле чертежа проводим прямую, на которой откладываем последовательно от произвольной точки I равные отрезки I – II, II – III,… (рис. 6.9 б).

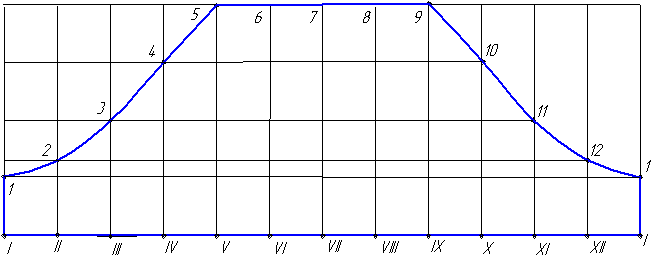
4. Через точки I, II, III,… проводим перпендикуляры к прямой и на них откладываем длины соответствующих образующих цилиндра, получаем точки 1, 2, 3 и т. д.

5. Соединив точки на концах образующих, расположенные на участке V – IX прямой, а на остальных участках – плавной кривой, получаем развертку боковой поверхности усеченного цилиндра.

а б

Рис. 6.9

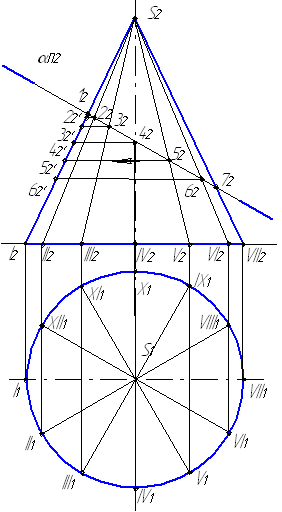
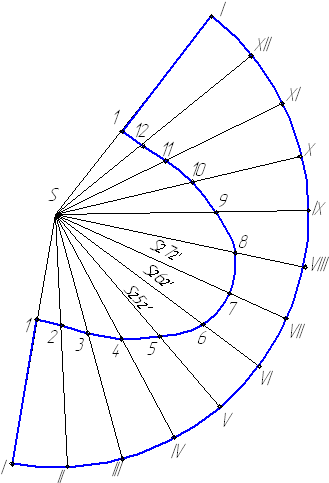
Пример 6.6. Построить развертку боковой поверхности кругового конуса, усеченного плоскостью α (рис. 6.10 а, б).

Развертка конуса – это сектор окружности радиусом, равным длине образующей конуса.

а б

Рис. 6.10

1. Делим основание конуса на 12 равных частей и проводим через точки деления горизонтальные и фронтальные проекции образующих конуса (рис. 6.10,а). Определяем точки их пересечения с плоскостью α.

2. Строим развертку боковой поверхности полного конуса (рис. 6.10 б). Из произвольной точки S на свободном месте поля чертежа проводим дугу окружности радиусом, равным длине образующей конуса. Откладываем последовательно из произвольной точки на дуге 12 дуг, хорды которых равны стороне 12-угольника. Проводим образующие конуса.

3. На каждой образующей откладываем натуральную величину длины отрезка соответствующей образующей конуса от его вершины до точки пересечения с плоскостью α. Натуральная величина отрезков находится вращением вокруг горизонтально-проецирующей оси.

4. Концы отрезков соединяем плавной кривой. Развертка боковой поверхности конуса построена.

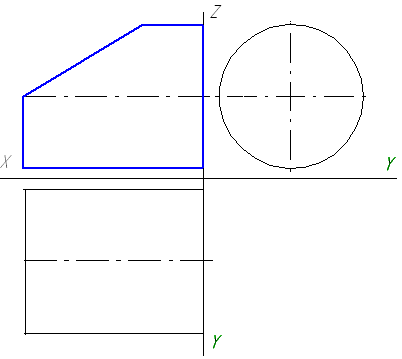
Задача 6.28. По фронтальной проекции усеченного прямого кругового цилиндра построить его горизонтальную и профильную проекции. Дать натуральный вид сечения и полную развертку тела.

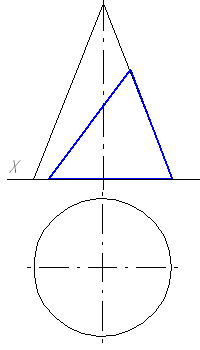
Задача 6.29. По фронтальной проекции усеченного конуса построить его горизонтальную проекцию. Дать натуральный вид сечения и полную развертку тела.