6.2. Пересечение поверхности вращения прямой линией

Для отыскания точек пересечения прямой с поверхностью вращения применяется метод вспомогательной секущей плоскости, которая проводится через рассматриваемую прямую так, чтобы получить простейшую фигуру сечения. .

Пример 6.1. Построить проекции точек пересечения отрезка прямой АВ с поверхностью одной четвертой части открытого тора. Определить видимость отрезка. M, N = AB ∩ Ф - ? (рис. 6.5)

1

. Через отрезок АВ проведем вспомогательную секущую плоскость α. Плоскость α выбираем перпендикулярно оси открытого тора АВ  α, α  I, α || П₂.

2. Плоскость α пересекает поверхность по кольцу радиусом (R, R').

3. Отрезок АВ пересекается с сечением в точках M и N, которые являются искомыми точками пересечения отрезка с поверхностью тора.

4. В горизонтальной проекции точка М₁ видна, так как расположена над экватором тора, точка N₁ не видна. Во фронтальной проекции точки M₂ и N₂ не видны, они расположены на задней части поверхности.

Рис. 6.5

П

ример 6.2. Найти проекции точек пересечения прямой общего положения с конусом (рис. 6.6).

1. Проводим через прямую d горизонтально-проецирующую плоскость.

2. Горизонтальная проекция линии пересечения плоскости и конуса совпадает с d₁ и α₁. Для построения фронтальной проекции этой линии достаточно определить проекции нескольких точек. Характерные точки 1₁, 2₁ лежат на основании конуса, точка 3₁ расположена на образующей S₁В₁. Берем промежуточную точку 4₁. Для их построения используют правила построения проекций точек на поверхности. Соединяем точки 1_2, 4₂, 3₂, 2₂ . Имеем фронтальную проекцию линии пересечения горизонтально-проецирующей плоскости α и конуса.

3

Рис. 6.6

. d₂ ∩ (1₂ 4₂ 3₂ 2₂) = M₂ и N₂ – фронтальные проекции точек пересечения прямой с конусом. По линиям связи получаем горизонтальные проекции точек – M₁ и N₁.

4. Определяем видимость прямой d.

Задачи 6.5, 6.6. Построить проекции точек пересечения отрезка MN с поверхностью закрытого тора, сферы.
Задачи 6.7, 6.8. Построить проекции точек пересечения отрезка прямой АВ с поверхностью конуса, сферы.
Задачи 6.9, 6.10. Построить проекции точек пересечения отрезка прямой АВ с поверхностью тора, цилиндра.
Задача 6.11, 6.12. Построить проекции точек пересечения прямой MN с поверхностью закрытого тора, наклонного конуса.

6.3. Пересечение поверхности вращения плоскостью

Линия пересечения поверхности вращения плоскостью определяется по точкам пересечения параллелей (или образующих) поверхности вращения с плоскостью. Определяют главные, характерные точки линии пересечения и промежуточные точки. К главным линиям относятся точки пересечения с плоскостью главного меридиана поверхности, экватора поверхности, а также высшая и низшая точки линии пересечения относительно плоскости, перпендикулярной оси поверхности вращения.

В зависимости от положения секущей плоскости линия пересечения с поверхностью вращения имеет разную форму.

Цилиндр (прямой). Если секущая плоскость параллельна основанию, то линия пересечения – окружность; расположена под углом к основанию – эллипс; перпендикулярна основанию – прямоугольник.

Сфера. Независимо от положения секущей плоскости линия пересечения – окружность.

Тор. Если секущая плоскость перпендикулярна оси тора, то в сечении получается кольцо (в частном случае круг); расположена под другим углом к оси – две окружности, два эллипса, один эллипс, или по форме похожа на цифру «8».

Конус (прямой). Если секущая плоскость параллельна основанию, то линия пересечения – окружность; пересекает две образующих конуса – эллипс; параллельна образующей – парабола; пересекает одну образующую – гипербола; проходит через вершину конуса – треугольник.

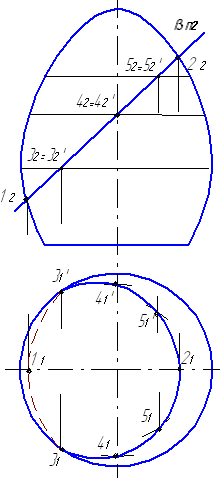
Пример 6.3. Построить проекции линии поверхности вращения с фронтально-проецирующей плоскостью β (рис. 6.7).

1. Главными точками линии пересечения являются точки 1 и 2, принадлежащие главному меридиану поверхности, а также точки 3 и 3', в которых экватор поверхности пересекается с плоскостью β. Точки 1 и 2 являются одновременно низшей и высшей точками линии пересечения.

2. Произвольно выбранные параллели поверхности пересекаются с плоскостью β в точках 4, 4', 5 и 5'. Соединив в горизонтальной проекции найденные точки плавной кривой, получим горизонтальную проекцию линии пересечения.

Фронтальная проекция является отрезком 1₂ – 2₂ на следе β_П2 плоскости β.

3

Рис. 6.7

. Определяем видимость линии пересечения. Часть линии пересечения, которая расположена выше экватора, является видимой на горизонтальной проекции.

Графические построения проекции линии пересечения поверхности вращения плоскостью значительно проще, если плоскость проецирующая.

Пример 6.4. Построить проекции конуса, усеченного заданными плоскостями (рис. 6.8).

1. Горизонтальные проекции характерных точек 1, 2, 3, 4, 5, расположенных на поверхности конуса определяем по правилам построения проекций точек на поверхности. Например, проекция точки 1₁ строится так: через точку 1₂ проводим горизонтальную прямую до пересечения с контуром конуса в точке 6₂, затем радиусом S₁6₁ проводим дугу окружности и на ней по линии связи с точкой 1₂ находим точку 1₁.

2. Выбираем по необходимости промежуточные точки, строим их проекции.

3. Соединяем полученные горизонтальные проекции точек. Линия пересечения представляет собой на участках: S1 – отрезок прямой; 12 – дугу окружности; 23 – участок параболы; 34 – участок эллипса; 45 – гиперболу.

4

. Профильную проекцию строим на основании правила взаимосвязи проекций. При этом необходимо учесть контурные точки 7,8, профильные проекции которых лежат на контуре S₃A₃. Участок образующей SA между точками 7 и 8 «вырезан» секущими плоскостями.

Относительно осей Ф₁ и Ф₃ получаем симметричную картинку, поэтому достаточно построить проекции на половине конуса.

Невидимые проекции линий пересечения секущих плоскостей показываем штриховой линией.

Рис. 6.8

Задачи 6.13 – 6.15. Построить проекции сечения конуса вращения проецирующей плоскостью β.

Задача 6.16. Построить проекции сечения тора проецирующей плоскостью α.

Задачи 6.17, 6.18. Построить сечения тора проецирующей плоскостью α.

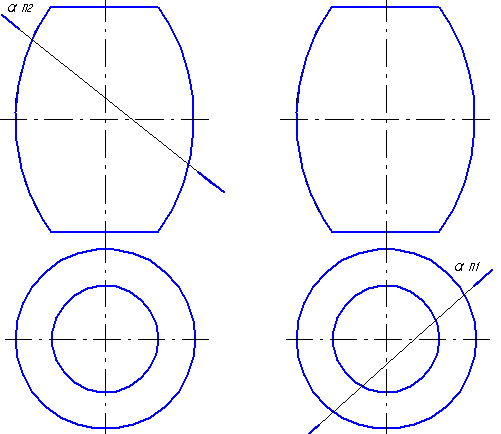
Задачи 6.19, 6.20. Построить проекции сечения тора, сферы проецирующей плоскостью α.

Задачи 6.21, 6.22. Построить проекции сечения тора проецирующей плоскостью α.

Задача 6.23. Построить проекции сечения цилиндра плоскостью β.

Задача 6.24. Построить проекции сечения конуса плоскостью α.

З адача 6.25. По фронтальной проекции цилиндра с вырезом построить его горизонтальную и профильную проекции.

Задача 6.26. По фронтальной проекции конуса с вырезом построить его горизонтальную и профильную проекции.

З

адача 6.27. По фронтальной проекции сферы с вырезом построить ее горизонтальную и профильную проекции.