5.3. Развертки многогранников

Многогранные поверхности являются развертываемыми, так как могут быть совмещены с плоскостью без разрывов и складок.

Разверткой многогранника называется плоская фигура, составленная из его граней, совмещенных с одной плоскостью. При этом смежными будут две грани, имеющие общее ребро.

Все грани на развертке изображаются в натуральную величину, поэтому ее построение сводится к нахождению натуральных величин отдельных граней поверхности.

Для построения развертки призмы применяют два метода: нормального сечения и раскатки.

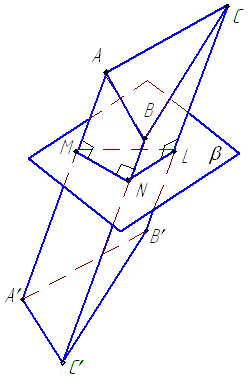
Метод нормального сечения. Нормальным сечением призмы называется ее сечение плоскостью β, перпендикулярной ребрам призмы (рис. 5.4 а). Такая плоскость пересекает призму по некоторому многоугольнику, в нашем случае треугольник MNL, стороны которого перпендикулярны ребрам призмы и равны расстояниям между соответствующими соседними ребрами призмы. Так АА'  MN, ВВ'  MN, ВВ'  NL. MN, NL и LM – соответственно расстояния между ребрами АА' и ВВ', ВВ' и СС', СС' и АА'.

Для построения развертки такой призмы сначала следует ее нормальное сечение MNL развернуть в прямую линию М₀М₀ (рис. 5.4 б). Затем провести к этой прямой в точках М₀, N₀, L₀ перпендикуляры, на которых соответственно отложить длины ребер от нормального сечения до вершин призмы: М₀А₀ = МА, М₀А₀' = МА' и т. д. Соединив полученные точки ломаными линиями, получим развертку боковой поверхности призмы.

Ч

тобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основания призмы – треугольники АВС и А'В'С', предварительно определив их натуральную величину.

а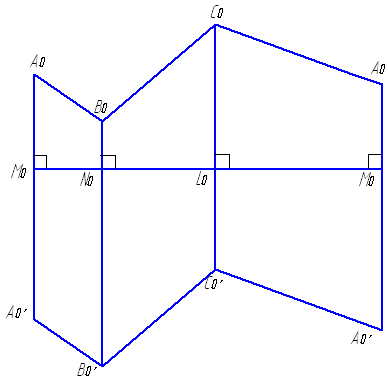

б

Рис. 5.4 а,б

Метод раскатки. Раскатываем боковую поверхность призмы на плоскости чертежа одну грань за другой.

Этот способ наиболее эффективен тогда, когда основание призмы проецируется в натуральную величину на плоскость проекций.

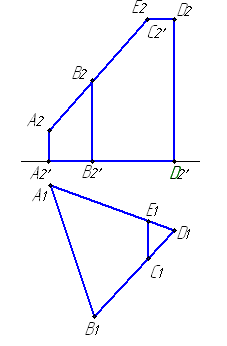
Пример 5.4. Построить развертку прямой пятиугольной призмы частного положения (рис. 5.5).

Рис.5.5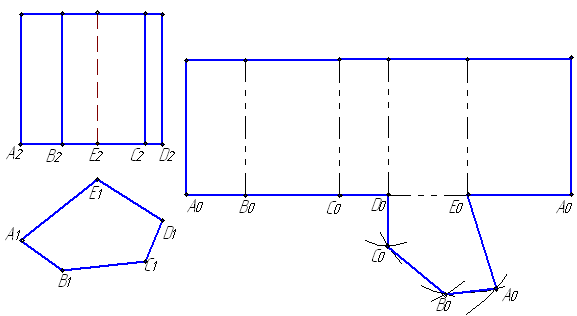

1. Ребра основания проецируются в натуральную величину на П₁, а длину боковых ребер измеряем на П₂.

2. Отметим в произвольном месте чертежа точку А₀ на горизонтальной линии. Строим последовательно В₀, С₀, D₀, E₀, A₀, перенося на эту линии длину отрезков A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁A₁. В результате раскатываем все боковые грани призмы.

3. Строим на одной из сторон, например D₀E₀, нижнее основание, применяя метод триангуляции. Аналогично строим верхнее основание.

Развертка полной пирамиды представляет собой совокупность основания пирамиды (многоугольник) и всех ее граней (треугольников). Для построения развертки боковой поверхности пирамиды в общем случае применяют метод треугольников (триангуляции), т.е. последовательно строят каждую боковую грань пирамиды.

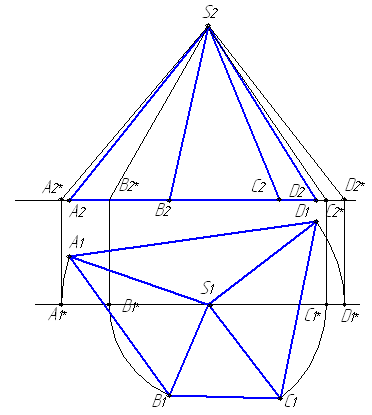
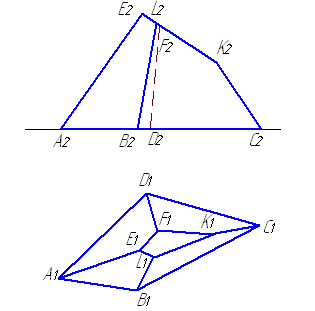
Пример 5.5. Построить развертку четырехугольной пирамиды SABCD (рис. 5.20 а,б).

1. Определяем натуральную величину ребер пирамиды. Натуральную величину каждого из боковых ребер находим способом вращения вокруг проецирующей оси, за которую принимаем горизонтально-проецирующую прямую, проходящую через вершину пирамиды S. Ребра приводим в положение фронталей и находим новые фронтальные проекции (рис. 5.6,а). Отрезки S₂A₂*, S₂B₂*, S₂C₂*, S₂D₂* - натуральные величины боковых ребер.

Н

Рис. 5.6 а

атуральная величина ребер основания пирамиды – длина их горизонтальных проекций, т.к. основание пирамиды занимает положение горизонтальной плоскости уровня.

2. Вычерчиваем первую грань SAB. Для этого свободном месте поля чертежа ставим точку S₀ (рис. 5.6,б). Через нее проводим прямую линию в произвольном направлении и на ней откладываем длину SA = S₂A₂*, получаем точку А₀.

Из точки А₀ проводим дугу окружности радиусом АВ = А₁В₁, а из точки S₀ радиусом SB = S₂B₂*. На их пересечении лежит точка В₀. Соединив точки S₀, A₀, B₀, получаем грань SAB.

3. Аналогично строим остальные боковые грани пирамиды.

4. Достраиваем к одному из ребер основания пирамиды четырехугольник A₁D₁C₁D₁ этим же способом.

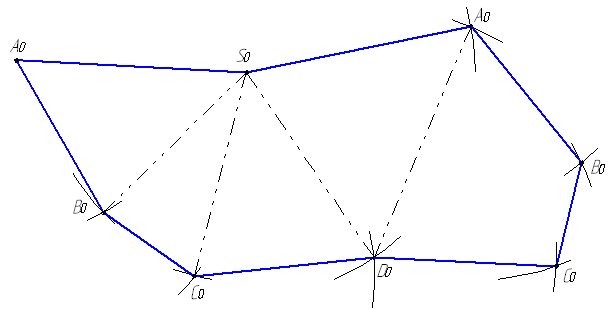
Рис. 5.6 б

Задача 5.14. Построить развертку усеченной треугольной призмы.

Задача 5.15. Построить развертку усеченной четырехугольной пирамиды.