2. Вращение вокруг проецирующих прямых

Этот способ является частным случаем плоскопараллельного перемещения: все точки геометрической фигуры перемещаются в пространстве также в плоскостях, параллельных плоскостям проекций, но не по произвольной траектории, а по окружностям.

Рис. 4.6 Рис. 4.7

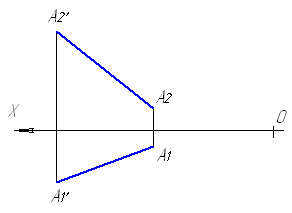
При повороте точки А вокруг горизонтально проецирующей оси I  П₁ на угол φ против часовой стрелки (рис. 4.6) точка А перемещается в плоскости   I   || П₁ по окружности радиуса R_А = I₁А₁. Горизонтальная проекция точки А₁ описывает дугу А₁А₁' окружности радиуса R_А с центральным углом φ. Фронтальная проекция точки А₂ движется по прямой, параллельной оси координат ОX (Z_A = const). Зная новое положение А₁', определяем ее фронтальную проекцию А₂'.

На рис. 4.7 показан поворот точки В вокруг фронтально проецирующей оси на угол ψ по часовой стрелке - I  П₂, В    I   || П₂, R_В = I₂B₂, Y_B = const.

Вращение прямой вокруг оси, пересекающей эту прямую, сводится к вращению какой-либо одной ее точки, поскольку точка пересечения прямой с осью вращения остается неподвижной.

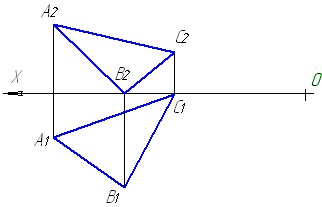
На рис. 4.8 отрезок АВ общего положения вращением вокруг оси

I  П₁  В  I приведен в положение, параллельное фронтальной плоскости проекций П₂ - А₂'В₂ || П₂, А₂'В₂ = |АВ|.

Рис. 4.8

5. Многогранники

Многогранником называется геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, которые являются его гранями (боковые грани, основания), а линии их пересечения – ребрами. Концы ребер называются вершинами многогранника. Наиболее распространенными видами многогранников являются прямые призмы и пирамиды.

5.1. Изображение многогранников

На ортогональном чертеже любой многогранник может быть задан проекциями его вершин (точками), ребер (отрезками прямых), и граней (плоскими фигурами).

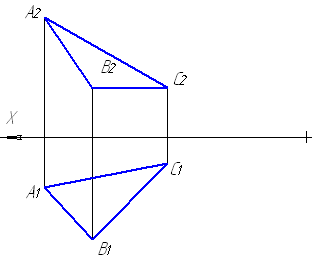
Пример 5.1. Построить проекции прямой призмы высотой 45 мм, стоящей на плоскости α, заданной следами. Основание призмы – равнобедренный треугольник АВС с основанием АВ || П₁ и равным 40 мм, высота CD – 25 мм (рис. 5.1).

Рис. 5.1

1. В плоскости строим основание призмы - ∆ АВС. На горизонтали А-1 откладываем А₁В₁ = |AB| = 40, A₁B₁ || OX. Высота треугольника CD лежит на линии ската D-2 плоскости α. Горизонтальная проекция С₁ вершины с определяется с помощью вспомогательного треугольника D₁2₁2*.

2. Строим боковые ребра призмы. Через точку А проводим отрезок АК, перпендикулярный плоскости. А₁К₁  α_П1, А₂К₂  α_П2. Точка К выбрана произвольно на данном направлении перпендикуляра к плоскости.

Определяем натуральную величину отрезка АК методом вспомогательного прямоугольного треугольника и на направлении его гипотенузы откладываем высоту призмы Н = 45мм и строим точку А' верхнего основания призмы. Ребра ВВ' и СС' параллельны и равны ребру АА'.

3. Видимость призмы на плоскостях проекций определяется по правилам: 1) Контур проекций многогранника всегда видимый.

2) Если внутри контура проекции пересекаются две прямые, то одна из них видима, а другая нет (применяется метод конкурирующих точек).

3) Если внутри контура проекции пересекаются три линии и одна из них видима, то и две остальные видимы и наоборот.

Задача 5.1. Построить проекции прямой призмы с основанием АВС, если дано ребро АА'. Стороны основания: АС || П1, и равна 40 мм, АВ || П2 и равна 30 мм. Определить видимость.

Задача 5.2. Построить проекции пирамиды с основанием АВС. Высота проходит центр треугольника и равна 40 мм. Определить видимость.

Задача 5.3. Построить проекции прямой призмы высотой 40 мм, зная проекции ее нижнего основания. Определить видимость.	Задача 5.4. Построить комплексный чертеж пирамиды и ломаную линию на ее поверхности.