
- •Кратні і криволінійні інтеграли
- •§1 Подвійний інтеграл
- •Поняття подвійного інтеграла.
- •§2. Геометричні застосуваання.
- •§3. Застосування подвійного інтеграла у фізиці.
- •§4 Потрійний інтеграл.
- •2.Геометричні та фізичні застосування потрійного інтегралу
- •§5 Криволінійні інтеграли.
- •Криволінійний інтеграл I роду.
- •Приклад:
- •Приклад 2
- •Формула Гріна (зв‘язок з подвійним інтегралом)
Кратні і криволінійні інтеграли
§1 Подвійний інтеграл
Поняття подвійного інтеграла.
Нехай функція
f(x,y)
завдана
на прямокутнику D:
a![]() x
b,
c
y
d.
x
b,
c
y
d.

 d
d

Dij
c

Xi-1 Xi
a b
Розіб`ємо
відрізок [a,b]
точками
x![]() =a+
=a+![]() i,
i,
![]() на
n
відрізків [x
на
n
відрізків [x![]() ;
x
],
i=0,n довжини
;
x
],
i=0,n довжини
![]() x
=
,
а відрізок [с,d],
точками
[y
;
y
],
x
=
,
а відрізок [с,d],
точками
[y
;
y
],
![]() ,
довжини
у
,
довжини
у![]() =
=![]() .
Таким
чином прямокутник D
розіб’ється
на
n
.
Таким
чином прямокутник D
розіб’ється
на
n![]() прямокутників
D
прямокутників
D![]() ,
площа
будь-якого з них
x
y
.
Складемо
інтегральну суму
,
площа
будь-якого з них
x
y
.
Складемо
інтегральну суму
(1) ![]() (
(![]() ,t
)
x
у
,
де
(
,t
)-
деяка точка прямокутника Dij.
,t
)
x
у
,
де
(
,t
)-
деяка точка прямокутника Dij.
Якщо
розглянемо границю виразу (1) коли n![]()
![]() ,
то отримаємо вираз
,
то отримаємо вираз
(2) ![]()
![]() (
,t
)
x
у
=
(
,t
)
x
у
=![]() dx
dy.
dx
dy.

О зн.1 Подвійним
інтегралом функції f(x,y)
називається
границя
зн.1 Подвійним
інтегралом функції f(x,y)
називається
границя
інтегральних сум по області D. (Вир.2)
Зауваження: інколи вираз dxdy пишуть як ds
Т еор.1 Якщо подвійні інтеграли від функцій f(x,y) і g(x,y) по
п рямокутнику
D
існують,
то для будь-яких чисел А і В виконується
рівність
рямокутнику
D
існують,
то для будь-яких чисел А і В виконується
рівність
(3) ![]() dx
dy=A
dx
dy=A![]() dxdy+
B
dxdy+
B![]() dxdy+B
dxdy+B
Дов. : Згідно з Озн.1 і властивостями границь послідовностей маємо:
![]() dx
dy=
dx
dy=
![]() (
,t
)
+Bg(
,t
))
(
,t
)
+Bg(
,t
))
x
у
=A
![]() (
,t
)
x
у
+B
(
,t
)
x
у
+B
![]() (
,t
)
x
у
(
,t
)
x
у
=A
![]() dxdy+B
dxdy+B![]() dxdy
dxdy
Щ.п.д.
Теор.2 Якщо
функція
f(x,y),
x![]() D,
a
x
b,
c
y
d
неперервна,
але вона
D,
a
x
b,
c
y
d
неперервна,
але вона
і нтегруєма у D.
(4) ![]() dxdy=
dxdy=![]() (
(![]() dx
dx
Дов. : Розіб’ємо відрізок [a,b] точками x на n рівних по довжині частин:
[x![]() x
],
тоді
(
dx=
x
],
тоді
(
dx=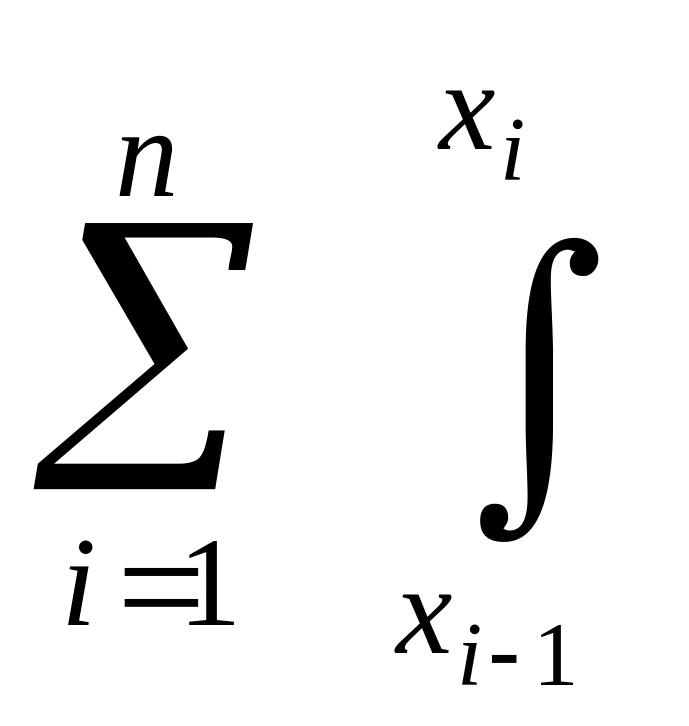 (
(![]() dx
dx
За
теоремою про середнє для інтегралів
існує
![]()
![]() ,
,![]() таке,
таке,
що
![]() (
dx=
(
dx=![]()
![]() .
.
Аналогічно
розіб’ємо
![]() і отримаємо:
і отримаємо:
![]()
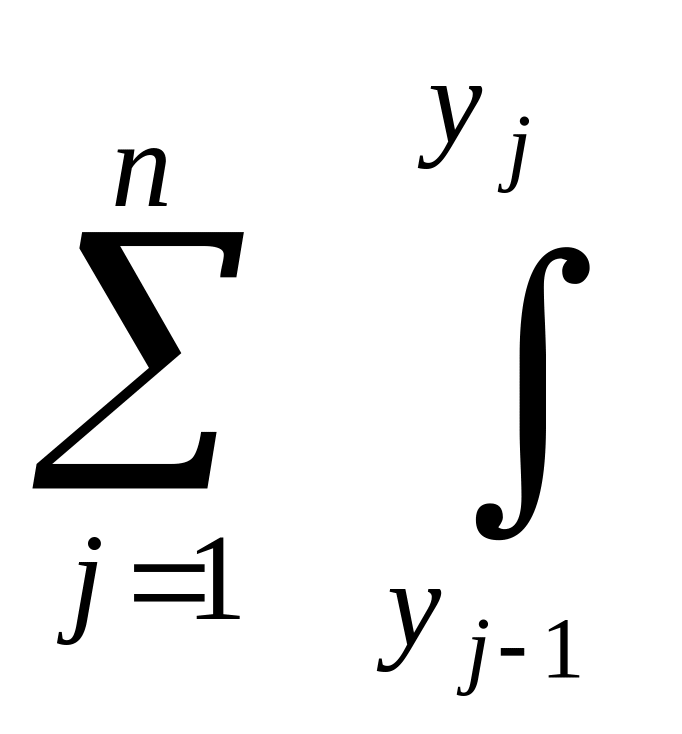 (
(![]()
![]() за
теоремою про середнє існує
за
теоремою про середнє існує
![]() таке, що
таке, що
![]()
![]() =
=![]() після чого
(
після чого
(![]()
Знайдемо
границю, коли
![]() і
отримаємо рівність (4)
і
отримаємо рівність (4)
Зауваження : Формула (4) – є формулою зведення подвійного інтегралу до повторного.
Таким чином:
(
 5)
5) ![]() dxdy=
dxdy=![]()
![]()


2. Подвійний інтеграл за будь-якою областю D
Нехай дана
![]() у де якій
обмеженій області
G
на
координатній площині .
у де якій
обмеженій області
G
на
координатній площині .

Y
 D
D
G
C

0 X
U B
Позначимо через
D
найменший прямокутник зі сторонами,
паралельними вісям. Розглянемо
![]() яка
співпадає з
в
т.
яка
співпадає з
в
т.
![]() за означенням
за означенням
За
означенням (6) ![]() dxdy=
dxdy
dxdy=
dxdy
Розглянемо
випадок, коли G
обмежена
зліва та справа відрізками
![]() ,
,
а знизу
та зверху графіками неперервних функцій
![]()
![]() тобто
G:
тобто
G:
![]() ,
тоді
,
тоді
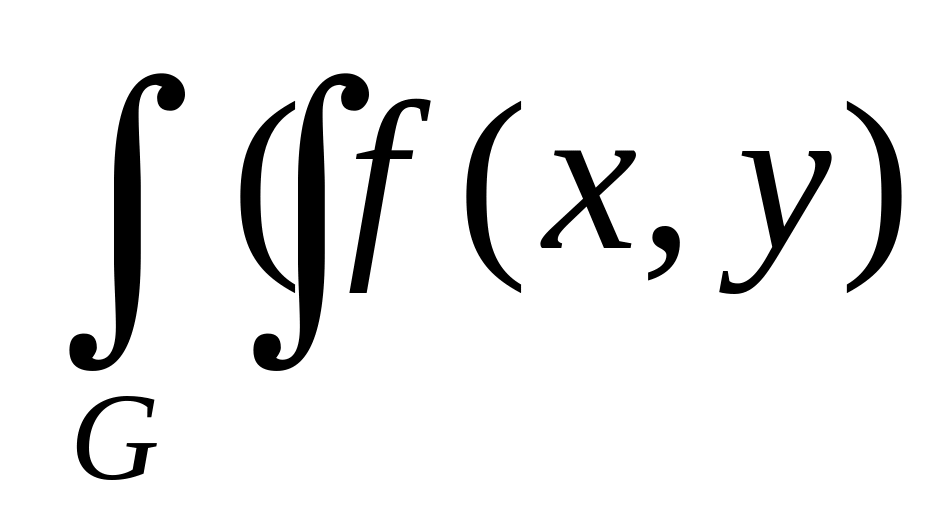 dxdy=
dxdy=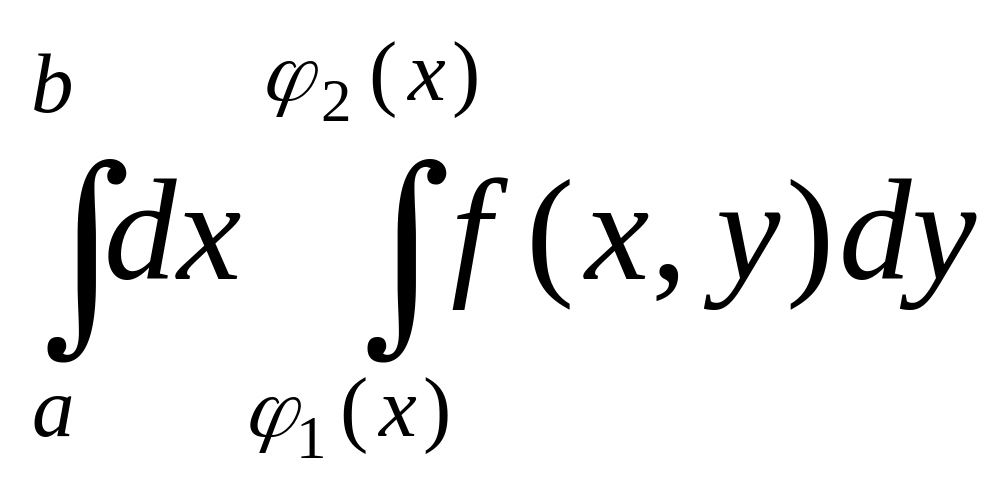

 Y2
Y2
G
Y1

a b
Аналогічно
розглянемо подвійний інтеграл , коли G
обмежена![]() ,
,
а
![]()
![]() =
=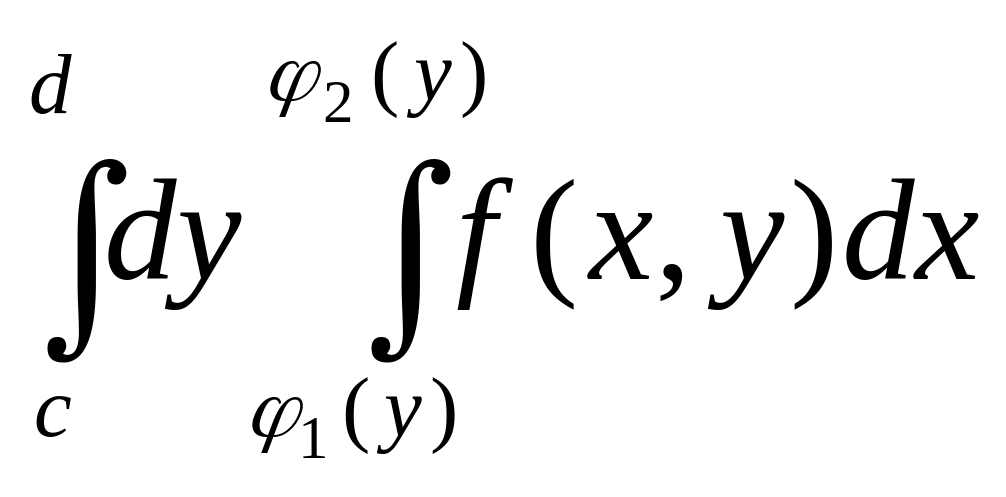
 D
D
G
C

Y1 Y2
a b
Приклад
:
Обчислимо
![]() ,
де
,
де
![]()
Відповідь
:
![]()
3 Заміна змінних у подвійному інтегралі.
Нехай
потрібно обчислити
![]() та
та
![]() взаємно однозначні функції.
взаємно однозначні функції.
V

G `
M `
U
Y
G
M
X
Координати
![]() називаються криволінійними координатами
т.М, таким чином:
називаються криволінійними координатами
т.М, таким чином:
=
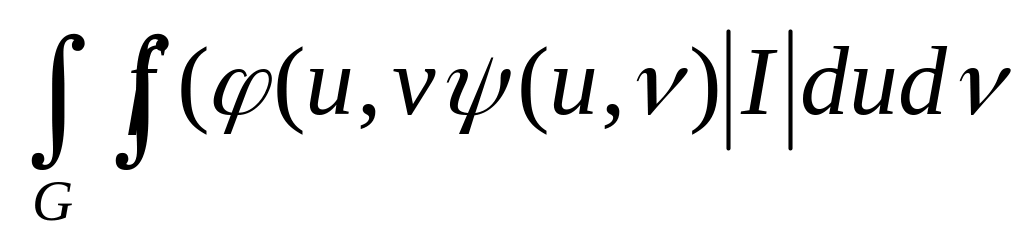 , де
, де
![]() -
визначник Острограцького (Якобіан
перетворення).
-
визначник Острограцького (Якобіан
перетворення).
Коли х і у мають неперервні частинні похідні 1-го порядку по u та v,
то між елементами
площі на площині ХОУ та на площині UOV
існує
зв‘язок
![]() ,
його геометричний зміст розглянемо,
коли в площині UOV
завдано прямокутник.
,
його геометричний зміст розглянемо,
коли в площині UOV
завдано прямокутник.
V

DV
DU U

Y
V+DV=const
V=const
0 X
Цей прямокутник
за допомогою перетворення![]() переходить в деяку криволінійну фігуру
на площині ХОУ. Цю фігуру при малих du
та dv
можна вважати паралелограмом і тоді
площа ії
переходить в деяку криволінійну фігуру
на площині ХОУ. Цю фігуру при малих du
та dv
можна вважати паралелограмом і тоді
площа ії
![]() .
.
З другого
боку, dudv
- це площа
елементарного прямокутника на площині
UOV
т.ч.
![]() є коефіцієнтом, що враховує зміну форми
елементарного прямокутника при переході
від декартових до криволінійних
координат. Тому його часто називають
коефіцієнт спотворення форм.
є коефіцієнтом, що враховує зміну форми
елементарного прямокутника при переході
від декартових до криволінійних
координат. Тому його часто називають
коефіцієнт спотворення форм.
Досить поширеними криволінійними координатами є полярні.
О зн. Полярними
координатами на площині називається
пара чисел (
зн. Полярними
координатами на площині називається
пара чисел (![]() )
де
)
де
![]() -
віддаль від точки до полюса, а
-
віддаль від точки до полюса, а
![]() -
кут між радіусом- вектором точки та
полярною віссю.
-
кут між радіусом- вектором точки та
полярною віссю.
Y


 S
S
0 X
![]() cos
cos
![]() sin
sin
Знайдемо перетворення Якобіану:
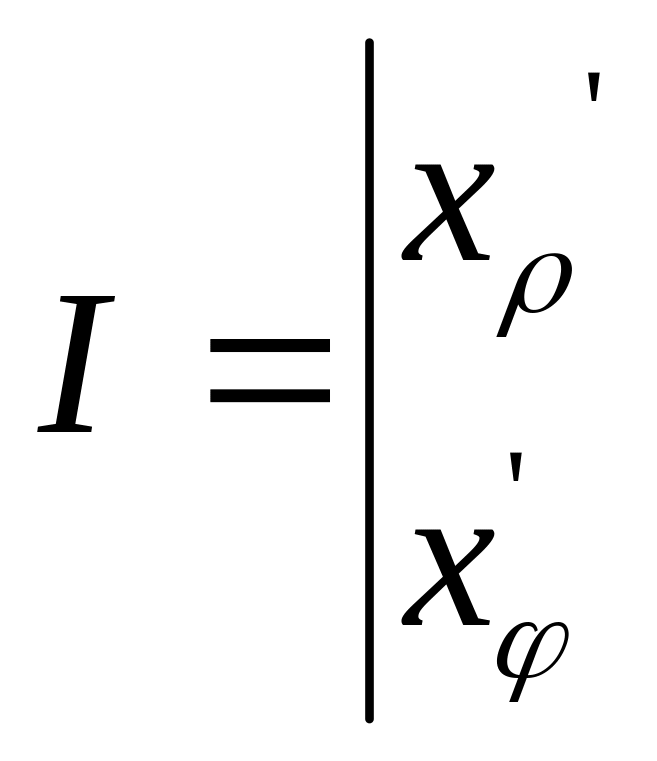


![]() =
=
![]() =
=
![]()
Т.ч.
![]() (9)
(9)
Приклад:
Переходячи до полярних координат
обчислити:![]()
D: частина кола R=1 C(0,0)
![]() dxdy=
dxdy=![]() =
=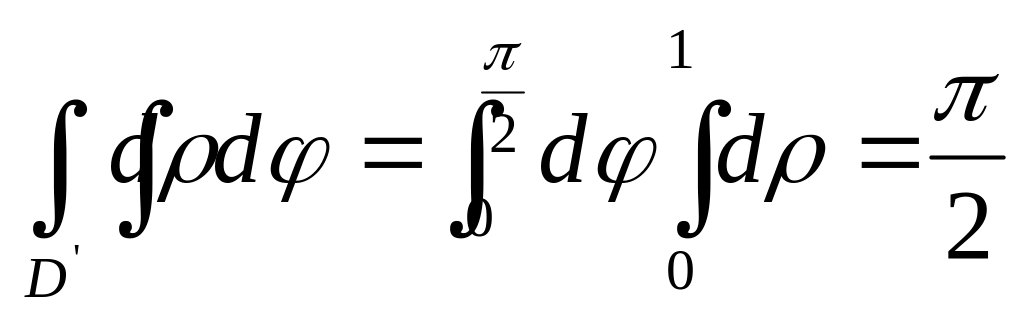
 1
1

0 1
