Яблонский К2 вариант 9

2

1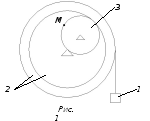. Исходные данные.

Радиусы:

R₂ = 40 см, r₂ = 30 см, R₃ = 15 см

Координаты и скорости груза 1:

x₀ = 10 см, ₀ = 7 см/с, x₂ = 48 см

Расчетные моменты времени:

t₁ = 1 c, t₂ = 2 c

2. Решение.

Уравнение движения груза 1 имеет вид

x = c₂t ² + c₁t + c₀

Коэффициенты с₀, с₁ и с₂ могут быть определены из следующих условий:

при t = 0 c₀ = x₀ = 10 см

при t₂ = 2 c 48 = 4с₂ + 14 + 10

с₂ = 6 см/с²

Скорость груза 1

 = x’ = 2c₂t + c₁

при t = 0 c₁ = ₀ = 7 см/с

 уравнение движения груза 1

x = 6t ² + 7t + 10

уравнение скорости груза 1

 = x’ = 12t + 7

уравнение ускорения груза 1

a = x” = 12 см/с ²

Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза  и угловые скорости колес ₂ и ₃.

В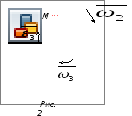 соответствии со схемой механизма (рис. 2)

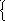
 = ₂R₂

₂ r₂ = ₃R₃

откуда

₃ = = = =

= 0,6t + 0,35

Угловое ускорение колеса 3

₃ = ₃’ = 0,6 рад/с ²

Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам

_М = ₃R₃ = (0,6t + 0,35)  15 = 9t + 5,25

при t₁ = 1 c _М = 14,25 см/с

a_М ^в = R₃ ₃ = 15  0,6 = 9 см/с ²

a_M ^ц = R₃ ₃ ² = 15  0,9 = 13,5 см/с ²

a_M = = R₃= 15  =

= 16,22 см/с ²

3. Ответы

, см/с	a, см/с 2	3, рад/с	3, рад/с 2	М, см/с	aM ц, см/с 2	aM в, см/с 2	aM, см/с 2
19	12	0,95	0,6	14,25	13,5	9	16,22