2.Расходная характеристика.
Итак, мы построили сопло, которое при заданных входных и выходных параметрах будет работать в расчетном режиме. Но противодавление на выходе не обязательно должно обеспечивать работу сопла в расчетном режиме с расчетным расходом. Построим теперь для нашего, уже спроектированного сопла, расходную характеристику в зависимости от выходного давления (см. рис.3).
Будем
откладывать по оси абсцисс безразмерное
давление
,
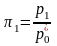а по оси ординат безразмерный приведенный
массовый расход
.
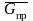Приведенный массовый расход получается из обычного массового расхода, записанного в форме (18), если «убрать» параметры торможения:
.
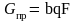(25)
Чтобы теперь получить безразмерный приведенный расход, необходимо поделить (нормировать) приведенный расход на его максимальное значение, а максимальным, очевидно, будет расход в расчетном режиме
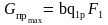(26)
(У площади выходного сечения индекс
расчетного режима «р» не ставится, т.к.
сопло уже построено, площади его сечений,
в том числе выходного, не меняются).
Тогда безразмерный приведенный расход
.
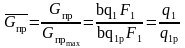Таким
образом, нужно построить зависимость
,
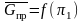и полученное нами соотношение:
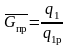(27)
позволяет составить план построения этого графика.
1.Если
выходное давление
,
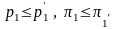в сопле наступает режим запирания;
возмущения из расширяющейся части сопла
перестают проходить за горло в суживающуюся
часть, течение газа в области от входа
до горла перестает зависеть от выходного
давления, в том числе перестает меняться
расход. Это постоянное значение расхода
совпадает с максимальным расходом
расчетного режима, безразмерный
приведенный расход равен единице:
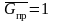при
.
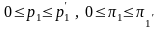2.Если
выходное давление
,
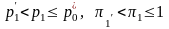режим течения нерасчетный, расход
меньше максимального и определяется
формулой (27). Для построения этой
ниспадающей части графика необходимо:
1)в
интервале давлений
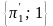выбрать
5 – 7 значений безразмерного давления
p;
например, если
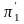=0.985,
то удобно взять в промежутке {0.985-1}
безразмерные давления
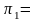0.987,
0.9901, 0.9929, 0.9953, 0.9971, 0.9986, 0.9995 (см. таблицу
газодинамических функций);
2)по
таблице определить функцию тока
,
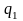соответствующую выбранному давлению
,
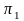затем найти отношение
, и на графике отметить очередную точку.
Осталось
выяснить, откуда возьмется давление
,
если нам известно безразмерное давление
расчетного режима
.
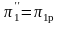Функция
тока q
– двузначная; одно и то же значение
функции тока получается при двух
значениях числа Маха (одно число Маха
соответствует дозвуковому режиму
течения, другое – сверхзвуковому),
следовательно, одному значению функции
тока соответствуют два безразмерных
давления. Ситуация, при которой в горле
сопла достигается звуковой режим,
наступает режим запирания, расход
достигает своего максимального значения,
а функция тока на выходе принимает
значение
,
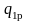наблюдается при двух выходных давлениях:
и
.
Следовательно, определить
можно так: найдя по
в таблице расчетную функцию тока
, ищем в столбце функций тока q
(двигаясь вверх, к началу таблицы) второе
такое же (или максимально близкое к
нему) значение. Второе безразмерное
давление, соответствующее той же функции
тока и будет нашим
.
Например, если
=0.2
(ближайшее табличное значение p=0.1985),
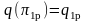=0.7404;
двигаясь вверх, находим второе максимально
близкое к
значение функции тока q=0.7419,
которому соответствует давление
p=0.8455.
Это и будет искомое
.