
Рабочие тетради №2-9 / Рабочая тетрадь_7
.doc|
7
71 Корреляционная связь (частный случай стохастической) – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами. Изучение корреляционных связей сводится в основном к решению следующих задач:
Задача корреляционного анализа – измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние. Задача регрессионного анализа – выбор типа модели (формы связи), устанавливающих степени влияния независимых переменных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
72 Различают:
К простейшим показателям тесноты связи относятся:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
73 Коэффициент
Фехнера (коэффициент корреляции
знаков) основан на сравнении поведения
отклонений индивидуальных значений
каждого признака (х и у) от
своей средней величины. При этом во
внимание принимаются не величины
отклонений (
Как
и любой показатель тесноты связи
коэффициент Фехнера может принимать
значения от –1 до +1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П
74 Таблица 7.1
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
7
75 Линейный коэффициент корреляции представляет собой среднюю величину из произведений нормированных отклонений для х и у:
Числитель формулы (7.3), деленный на n, т.е.
представляет собой среднее произведение отклонений значений признаков от их средних, именуемое ковариацией. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
М
76
где a1 – коэффициент регрессии в уравнении связи (см. подраздел 7.2).
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Л
77 Таблица 7.2 Оценка линейного коэффициента корреляции
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
О
78 Для достаточно большого числа наблюдений (n>50):
Если
При небольшом числе наблюдений (n<30)
Определяется расчетное значение t-критерия Стьюдента:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
79 Таблица 7.3
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Е
80
млн. руб. Рис. 7.1. Диаграмма рассеяния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р
81
Рассчитываем линейный коэффициент корреляции по формуле (7.5)
Расчетное значение t-критерия Стьюдента:
из ччего можно сделать вывод о значимости рассчитанного коэффициента корреляции.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
82 7.2.1. Парная регрессия
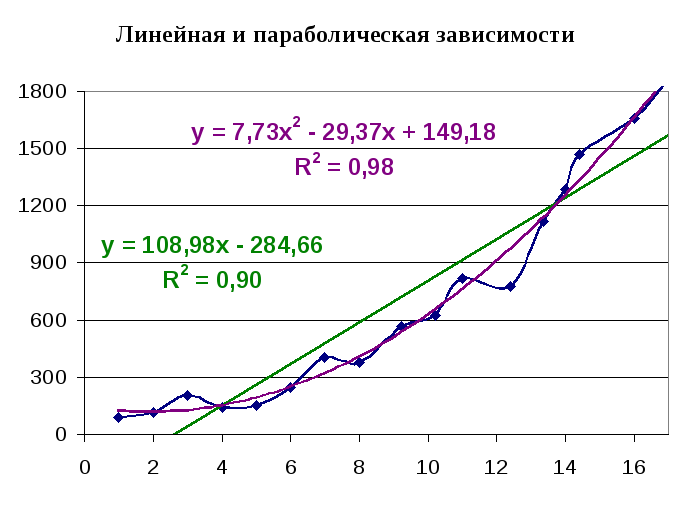
линейная
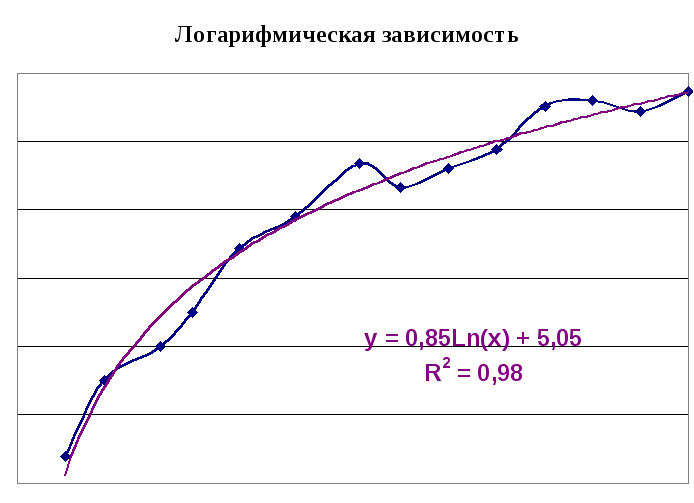
полулогарифмическая
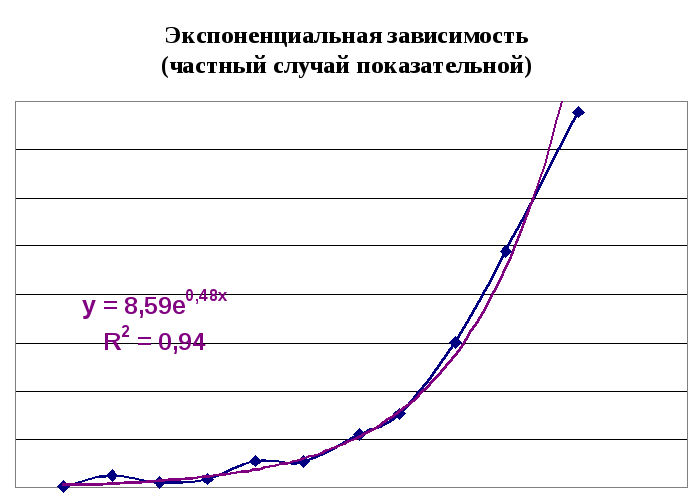
показательная
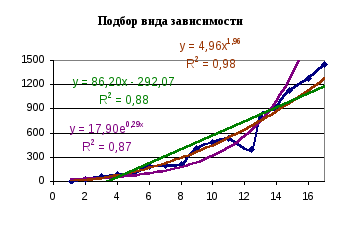
степенная
параболическая
гиперболическая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83 Для оценки параметров уравнений регрессии наиболее часто применяют метод наименьших квадратов (МНК)суть которого (для линейной зависимости):
Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении а0 и а1 функция двух переменных S может достигнуть минимума. Как известно для этого надо найти частные производные S по а0 и а1, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными. Найдем частные производные и приравняем их к нулю
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С
84
Отсюда можно выразить коэффициенты регрессии:
(7.21)
Коэффициент регрессии а0 иногда называют константой уравнения связи.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К
85
Для
линейной регрессии Более точно коэффициент эластичности определяют
где Для
линейной зависимости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

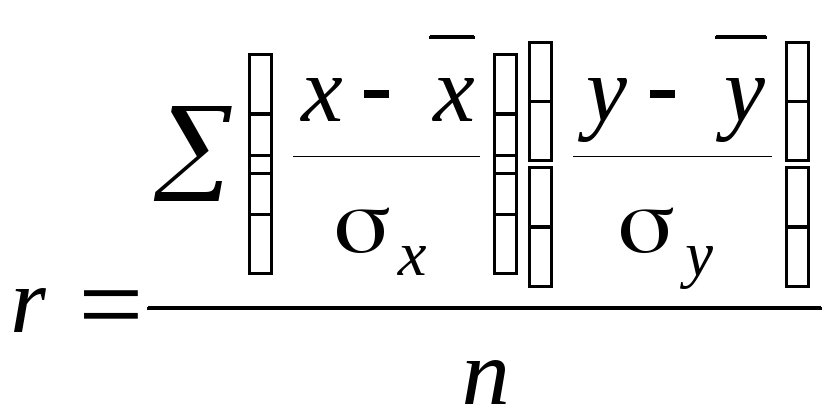 . (7.2)
. (7.2)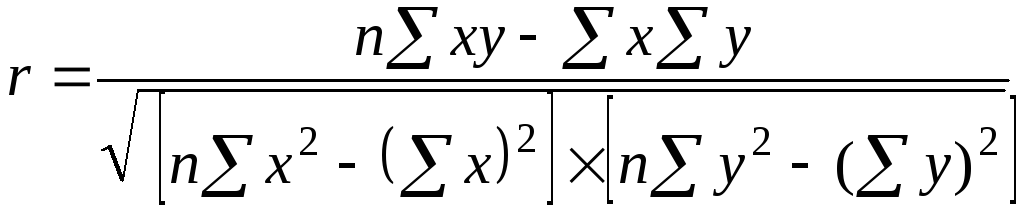 ; (7.6)
; (7.6)
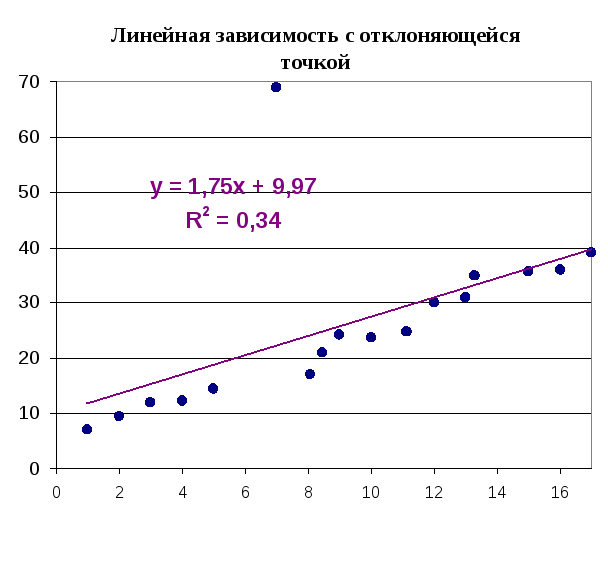
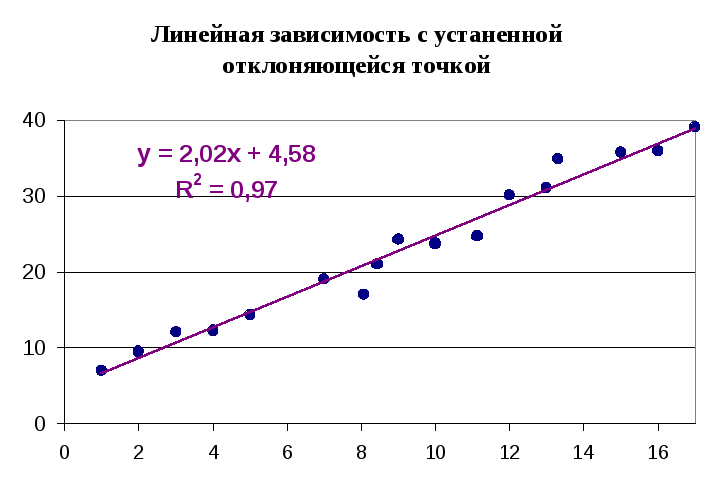
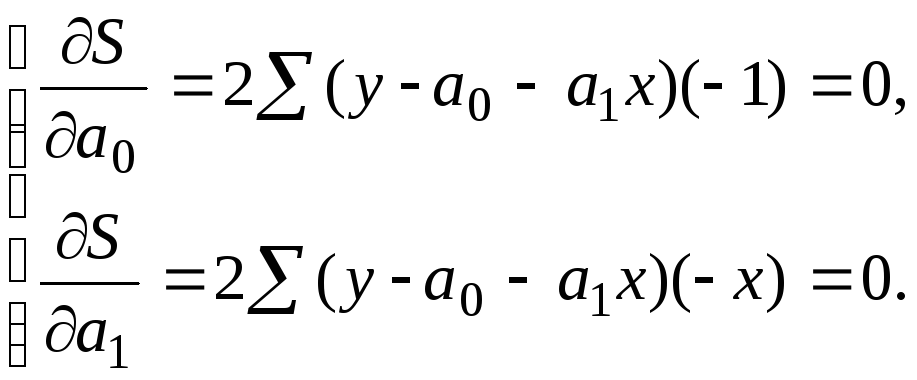 (7.19)
(7.19)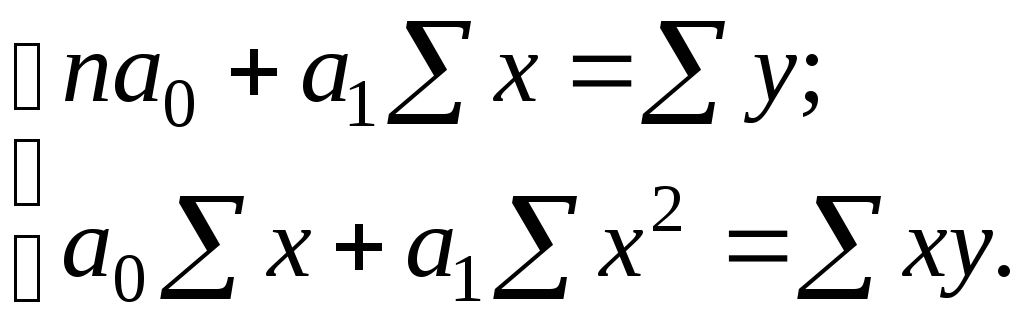 (7.20)
(7.20)