
Рабочие тетради №2-9 / Рабочая тетрадь_6
.doc|
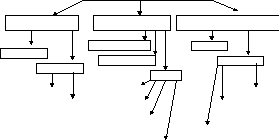
6. Генеральная и выборочная совокупность. 56 Виды статистических наблюдений
По времени проведения По источникам сведений По степени охвата совокупности
|
|
|
|||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|||||
|
|
|
6.1. Виды ошибок статистических наблюдений 57 Ошибкой статистического наблюдения считается величина отклонения между расчетным и фактическим значениями признаков изучаемых объектов. В зависимости от причин возникновения ошибок различают:
Причины возникновения ошибок:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2. Основы выборочного метода наблюдений 58 Виды выборки:
Используются два способа отбора:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
59
Неравенство Чебышева для любой случайной величины:
где M(X) – математическое ожидание; D(X) – дисперсия.
Формула
(6.1) устанавливает верхнюю границу
рассматриваемого события,
а (6.2) –
нижнюю границу вероятности события,
состоящего в том, что отклонения
значения случайной величины от
математического ожидания не превысит
(не будет менее) величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н
60
где
Эту вероятность в теореме А.М. Ляпунова (1901г.) используют для определения ошибки наблюдений.
где
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61 Если при измерениях отсутствует систематические погрешности, то M(Xi)=a при любом i. Тогда средняя арифметическая результатов и измерений сходится по вероятности к истинному значению a.
где а – истинное значение некоторой величины, значение которой надо измерить; Xi (i=1,2,…,n) – результат каждого измерения – случайная величина;
Дисперсия средней случайной величины Xi равна:
Среднее квадратическое отклонение ошибок выборки :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если
требуется оценить среднюю генеральной
совокупности
Для
выборки предельная ошибка
|
|
|
||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
|
|
63 При собственно-случайной выборке средняя квадратическая ошибка определяется по формулам:
|
|
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
64 Пример 6.1. В результате выборочного обследования жилищных условий жителей города на основе собственно случайной пятипроцентной бесповторной выборки, получен ряд распределения.
Определить
среднюю ошибку выборки
Решение:
Рассчитаем среднюю величину признака
где
N=2000
при 5% отборе, т.е.
|
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
Определить границы доли лиц, обеспеченность жильем которых составляет менее 10 м2. Численность доля в выборке таких лиц 103 чел.
65
Средняя
ошибка выборки:
Предельная ошибка выборки с P=0,954
Следовательно с вероятностью 0,95 можно утверждать, что в целом по городу доля лиц, имеющих менее 10 м2 на человека составляют от 8,4% до 12,2%. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66 Для серийной выборки ошибка при повторном отборе
где s – число серий; δ2 – межгрупповая дисперсия.
При
бесповторном отборе :
где S – общее число серий в генеральной совокупности.
Для механической выборки
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
|
6.4. Определение необходимой численности выборки 67 Для определения дисперсии признака:
При собственно-случайной выборке
|
|
|
|||||||||
|
|
|
||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|
68 Пример 6.2. Исходя из требований ГОСТа, необходимо установить оптимальный размер выборки из партии изделий 2000 штук, чтобы с вероятностью 0,997 предельная ошибка не превысила 3% от веса 500 гр. изделия (батона). Решение.
для
средней количественного признака
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
С
69 1) способ прямого пересчета Пример 6.3. Для исходных данных примера 6.2.
т.е. от 2000*0,04=80 шт. до 2000*0,16=320 шт. Пределы абсолютной численности нестандартных изделий в генеральной совокупности – от 80 до 320 шт.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
70 Например, если по данным выборки надо обследовать 50 человек, а по данным сплошных наблюдений получилось 52 (гнездовое наблюдение), то процент недоучета составит 52–50=2, тогда
где
Виды отбора:
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|

 ,
(6.4)
,
(6.4)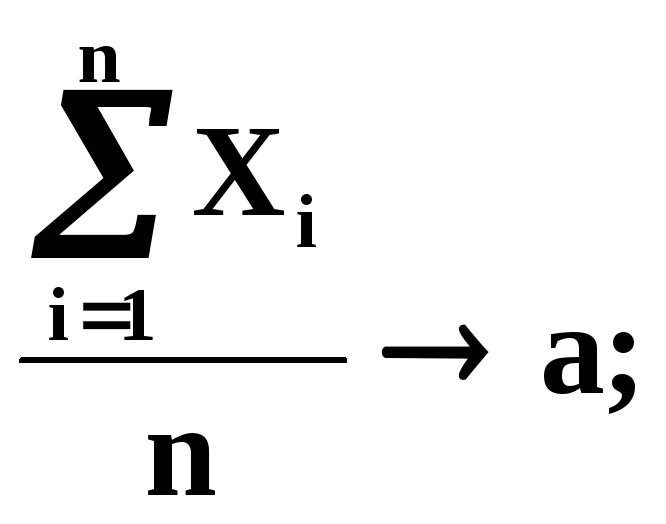 (6.5)
(6.5)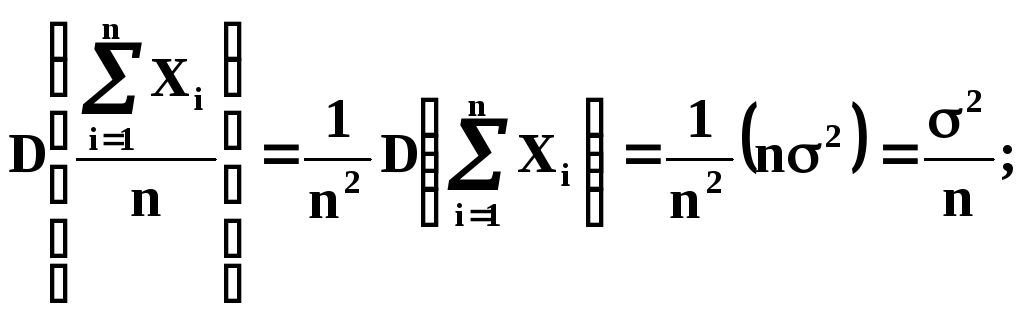 (6.6)
(6.6)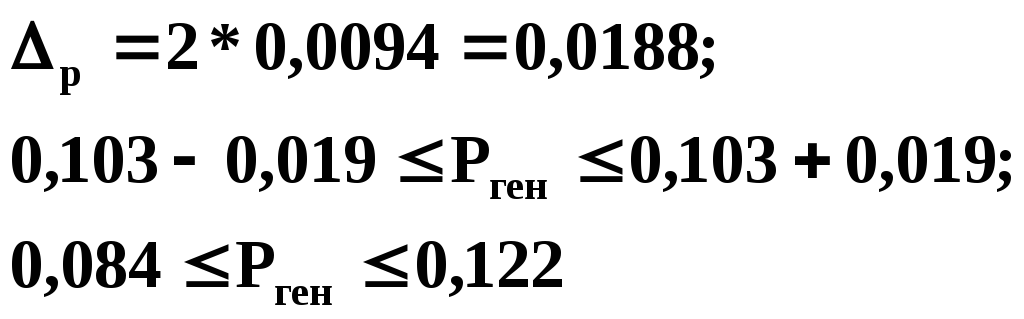
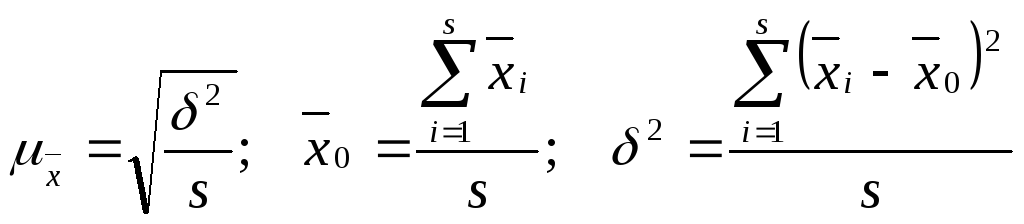 ,
(6.15)
,
(6.15)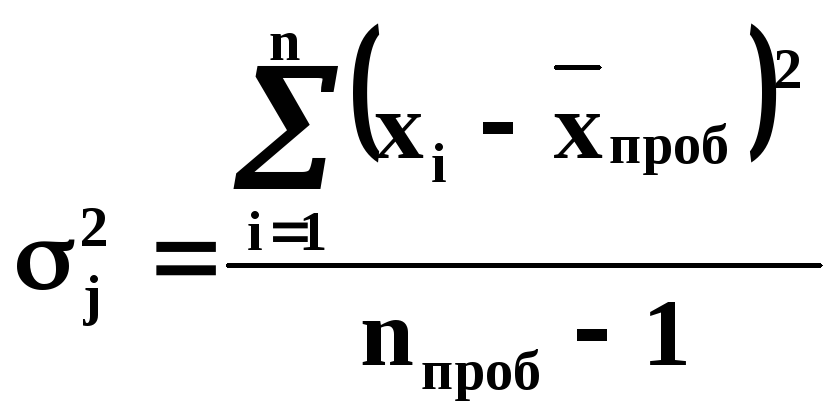 ,
где достаточно пробных наблюдений.
,
где достаточно пробных наблюдений.
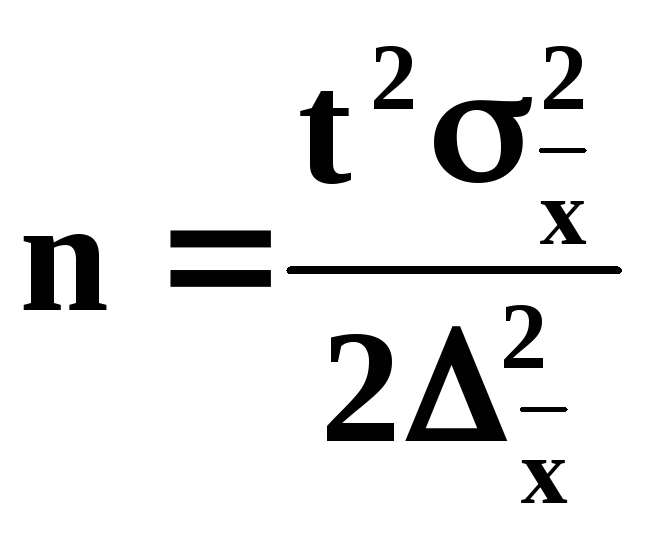 ,
(6.18)
,
(6.18)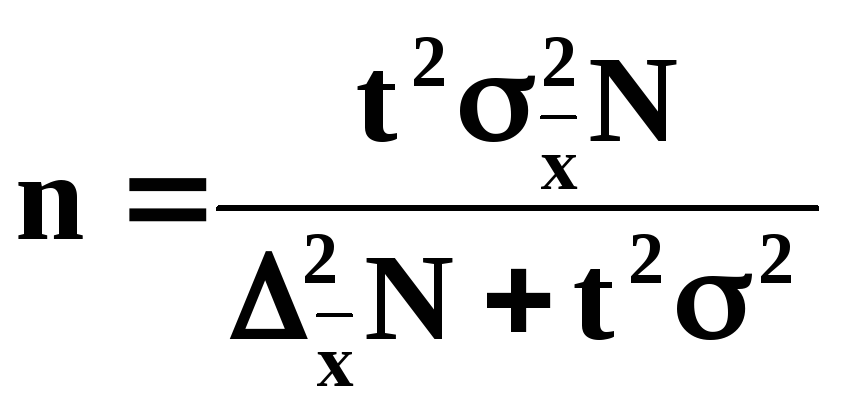 ,
(6.19)
,
(6.19)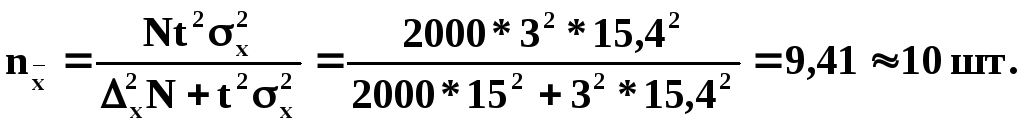
 , (6.22)
, (6.22)