Задание №2

Условие: Центральный вычислительный комплекс локальной компьютерной сети имеет 3 процессора и может одновременно обрабатывать 3 расчетных программы. Другие поступающие с терминалов пользователей программы могут храниться в памяти и выполняться по мере освобождения процессоров. Среднее число заявок, которые одновременно находятся в памяти, равно 5. Входной поток заявок простейший с интенсивностью 48 заявок в минуту. Время обработки программы случайное, распределено по показательному закону со средним значением 3 сек (t_обс.).

Задание:

1. Описать состояния СМО, построить граф состояний.

2. Найти вероятности состояний для стационарного случая и показатели эффективности работы комплекса. Проанализировать полученные результаты. Оценить работу комплекса.

3. Найти функциональную зависимость средней длины очереди от интенсивности входного потока и от среднего времени обслуживания .Представить зависимость в виде таблиц и графиков.

4. Один из процессоров не работает. Как организовать работу комплекса, чтобы не получить больших сбоев?

5. Найти оптимальное число процессоров, используя стоимостную функцию:

Известно, что с1=50 уе – затраты на введение в работу одного процессора, отнесенного к единице времени, с2 = 280 уе – стоимость производственных потерь от задержки выполнения программы в течение одной и той же единицы времени.

6. Выполнение срочного заказа увеличило интенсивность входного потока в 2 раза. Сколько процессоров нужно задействовать в комплексе, чтобы вероятность отказа возросла не более, чем в 1.5 раз?

Теоретическое введение.

Данная СМО – многоканальная система с ограниченной очередью.

Рассмотрим общий случай, найдем вероятности стационарных состояний СМО, оценим работу СМО. Пусть в СМО n каналов и m мест в очереди. Заявка, пришедшая в СМО, когда все места в очереди заняты, получает отказ. В этой СМО интересной характеристикой является вероятность отказа пришедшей заявке.

Запишем состояния системы СМО:

S₀ – в СМО нет заявок,

S₁ – в СМО одна заявка.

…………..

S_n – в СМО n заявок.

S_n+1 - в СМО n заявок в обслуживании, одна заявка в очереди.

………….

S_n+m – - в СМО n заявок в обслуживании, m заявки в очереди.

Следующая заявка, пришедшая в СМО, получает отказ.

Заметим, что число состояний конечно: S₀, S_1,…, S_n+m

Граф СМО приведен на рисунке 1:

Рис. 1

Вероятности состояний будут

(1)

Таким образом, если ≠ 1, то

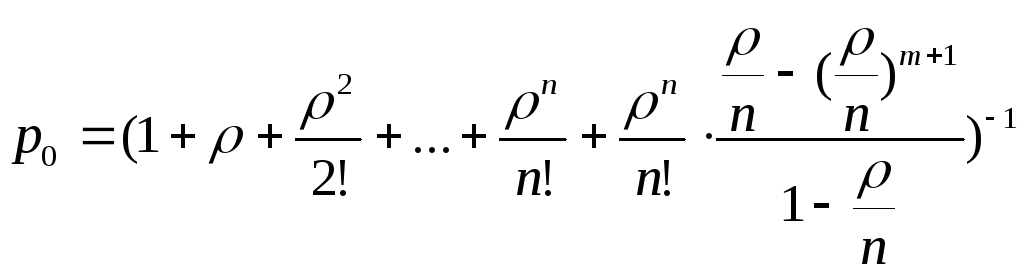
Если = 1, то расчетp₀ проводят по формулам:

;;…;; (2)

;…;. (3)

Таим образом, все вероятности системы найдены.

Найдем коэффициенты эффективности работы СМО:

(4)

(5)

Среднее число занятых каналов

(6)

Среднее число заявок в очереди

(7)

Среднее время ожидания

(8)

Среднее число заявок в системе

(9)

Среднее время нахождения заявки в системе

(10)

Чтобы найти оптимальное количество обслуживающих каналов для СМО с неограниченной очередью, используется стоимостная функция c(n), где n – число обслуживающих каналов. Ниже представлены виды стоимостных функций:

1. ,где n – число обслуживающих каналов, с1 – затраты на работу одного дополнительного канала в единицу времени, с2 – цена ожидания в единицу времени в расчете на одно требование, z_сист(n) – среднее число клиентов в СМО для каждого n.

2. , где n – число обслуживающих каналов, с1 – затраты на работу одного дополнительного канала, к единице времени, с2 – цена ожидания одной заявки в единицу времени, с3 – стоимостные потери от простоя одного канала в единицу времени, r₀(n) – среднее число заявок, стоящих в очереди, к_св(n) – среднее число свободных каналов.

3. ,где с1 – стоимостные потери из-за простоя одного клиента в СМО, t₁(n) – среднее время простоя одного клиента в СМО,

с2 – стоимость одного часа простоя канала СМО, t₂(n) – среднее время простоя канала.

Оптимальным будет считаться то число каналов, при котором значение стоимостной функции будет минимальным.