Глава 2. Аналитическая часть

Ι. Имеются данные о доходах населения РФ, млрд. руб.

Таблица № 1. Исходные данные.

Показатели	2000 год	2001 год	2002 год	2003 год
Доходы, млрд.руб.
оплата труда	2496,5	3421,4	3797,8	4139,6
социальные трансферты	551,1	808,3	897,2	977,9
доходы от собственности	270,9	304,6	338,1	368,5
доходы от предпринимательской деятельности	602,2	658,6	731,1	796,9
другие доходы	47,6	100,6	111,7	121,8

Источник: Российский статистический ежегодник.

Определить за каждый год:

1. номинальные и располагаемый денежные доходы населения;

2. прирост денег на руках у населения;

3. структуру денежных доходов населения;

4. индекс номинальных и располагаемых денежных доходов;

5. по данным условия и расчетным показателям определить: абсолютные приросты, темпы роста и представьте их в одной таблице.

Для анализа динамики доходов используют понятия номинальных, располагаемых и реальных располагаемых денежных доходов.

1. Номинальный денежный доход вычисляется по формуле:

Номинальный доход = начисленный доход

Номинальный доход =оплата труда + социальные трансферты +доходы от собственности + доходы от предпринимательской деятельности + другие доходы.

1.1. Номинальный доход:

в 2000 году = 2496,5 + 551,1 + 270,9 + 602,2 + 47,6 = 3968,3 (млрд. руб)

в 2001 году=3421,4+808,3+304,6+658,6+100,6=5293,5 (млрд. руб)

в 2002 году=3797,8+897,2+338,1+731,1+111,7=5875,9 (млрд. руб)

в 2003 году=4139,6+977,9+368,5+796,9+121,8=6404,7 (млрд. руб)

1.2. Располагаемый доход вычисляется по формуле:

Располагаемый доход= Номинальный доход – обязательные платежи и взносы*

*Таблица №2. Обязательные платежи и взносы.

Год	2000	2001	2002	2003
Обязательные платежи и взносы	309,8	473	648	784,1

Располагаемый доход:

в 2000 году = 3968,3 – 309,8 = 3658,5 (млрд. руб)

в 2001 году=5293,5-473=4820,5 (млрд. руб)

в 2002 году=5875,9-648=5227,9 (млрд. руб)

в 2003 году= 6404,7-784,1=5620,6 (млрд. руб)

2). Прирост денег на руках у населения.

Прирост денег на руках у населения = Располагаемый доход следующего года– Располагаемый доход предыдущего года

В 2001 году= 4820,5 – 3658,5=1162 (млрд. руб)

В 2002 году=5227,9-4820,5=407,4 (млрд. руб)

В 2003 году=5620,6-5227,9=392,7 (млрд. руб)

3). Динамика доходов изучается с помощью индексного метода. Вычислим индекс номинальных и располагаемых доходов:

Iноминальных доходов =Номинальный доход следующего года / Номинальный доход предыдущего года

Iноминальных доходов 2001= 5293, 5 / 3968,3 = 1,33

или 133 % - таким образом, номинальные доходы выросли на 33 %;

Iноминальных доходов 2002=5875,9 / 5293,5= 1,11

или 111 % - таким образом, номинальные доходы выросли на 11 %;

Iноминальных доходов 2003=6404,7 / 5875,9=1,09

или 109 % - таким образом, номинальные доходы выросли на 9 %;

Iрасполагаемых доходов=Располагаемый доход следующего года/ Располагаемый доход предыдущего года

Iрасполагаемых доходов в 2001 году = 4820, 5 / 3658,5 =1,317

или 131, 7 % -таким образом, располагаемые доходы населения выросли на 31,7%.

Iрасполагаемых доходов в 2002 году =5227,9 / 4820,5=1,08

или 108 % -таким образом, располагаемые доходы населения выросли на 8%.

Iрасполагаемых доходов в 2003 году =5620,6 / 5227,7=1,075

или 107,5 % -таким образом, располагаемые доходы населения выросли на 7,5%.

5). Вычислим абсолютные приросты и темпы роста. Результаты занесем в таблицу. Абсолютный прирост ΔΥ(цепной) определяется как разность между отчетным периодом y_i и предыдущим периодом y_i-1:

ΔΥ_ц= y_i – y_i-1

1). Оплата труда:

ΔYц 01 =3421,4-2496,5=924,9

ΔYц 02 =3797,8-3421,4=376,4

ΔYц 03 =4139,6-3797,8=341,8

2). Социальные трансферты:

ΔYц 01 =808,3-551,1=257,2

ΔYц 02 =897,2-808,3=88,9

ΔYц 03 =977,9-897,2=80,7

3) Доходы от собственности:

ΔYц 01 =304,6-270,9=33,7

ΔYц 02 =338,1-304,6=33,5

ΔYц 03 =368,5-338,1=30,4

4). Доходы от предпринимательской деятельности:

ΔYц 01 =658,6-602,2=56,4

ΔYц 02 =731,1-658,6=72,5

ΔYц 03 =796,9-731,1=65,8

5). Др. доходы:

ΔYц 01 =100,6-47,6=53

ΔYц 02 =111,7-100,6=11,1

ΔYц 03 =121,8-111,7=10,1

Темп роста Т(цепной) исчисляется делением показателя отчетного уровня y_i на уровень предшествующего ряда y_i-1,

T= y_i / y_i-1

1). Оплата труда:

Тц 01 =3421,4/2496,5=1,37

Тц 02 =3797,8/3421,4=1,11

Тц 03 =4139,6/3797,8=1,089

2). Социальные трансферты:

Тц 01 =808,3/551,1=1,466

Тц 02 =897,2/808,3=1,191

Тц 03 =977,9/897,2=1,08

3). Доходы от собственности:

Тц 01 =304,6/270,9=1,124

Тц 02 =338,1/304,6=1,109

Тц 03 =368,5/338,1=1,092

4). Доходы от предпринимательской деятельности:

Тц 01 ==658,6/602,2=1,093

Тц 02 =731,1/658,6=1,123

Тц 03 =796,9/731,1=1,081

5). Другие доходы:

Тц 01 =100,6/47,6=2,113

Тц 02 =111,7/100,6=1,11

Тц 03 =121,8/111,7=1,09

Таблица № 3.

Показатели	2000	2001	2002	2003	Абсолютный прирост (цепной) по годам			Темп роста (цепной) по годам в %
Доходы, млрд. руб.					01	02	03	01	02	03
оплата труда	2496,5	3421,4	3797,8	4139,6	924,9	376,4	341,8	137	111	108,9
социальные трансферты	551,1	808,3	897,2	977,9	257,2	88,9	80,7	146,6	119,1	108
доходы от собственности	270,9	304,6	338,1	368,5	33,7	33,5	30,4	112,4	110,9	109,2
доходы от предпринимательской деятельности	602,2	658,6	731,1	796,9	56,4	72,5	65,8	109,3	112,3	108,1
другие доходы	47,6	100,6	111,7	121,8	53	11,1	10,1	211,3	111	109

Имеются данные обследования бюджетов домашних хозяйств района:

Таблица № 4. Обследования бюджетов района

Группы домашних хозяйств	Среднедушевой доход, руб.	Число домохозяйств
1	До 500	5
2	500-1000	10
3	1000-1500	30
4	1500-2000	40
5	2000 и более	15

Определяем:

1. Среднедушевой доход;

2. Моду и медиану;

3. Коэффициент вариации.

Данный ряд сгруппирован по размеру среднедушевого дохода. Интервалы групп являются открытыми. Величина смежных интервалов (шаг интервала) равна 500. Перепишем данную таблицу, принимая для первого и последнего интервала шаг интервала, равный 500.

Для расчета данных таблицы используем табличный процессор Microsoft Excel пакета Microsoft Office 1997.

Таблица № 5. Шаблон выходной таблицы

Среднедушевой доход, руб. X	Число домохозяйств, fi	Середина интервала	Xifi	Сумма накопленных частот,S
А	1	2	3	4
До 500	5	250	=C18*B18	=B18
500-1000	10	750	=C19*B19	= СУММ (B18:B19)
1000-1500	30	1250	=C20*B20	= СУММ(B18:B20)
1500-2000	40	1750	=C21*B21	= СУММ (B18:B21)
2000 и более	15	2250	=C22*B22	СУММ (B18:B22)
Итого	=СУММ(B18:B22)		=СУММ(D18:D22)

Таблица № 6. Итоговая таблица

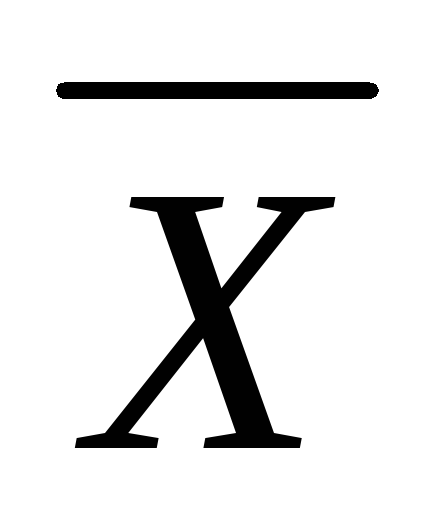№	Среднедушевой доход, руб. X	Число домохо зяйств, fi	Середина интервала	Xifi	Сумма накопленных частот, S
А	1	2	3	4	5
1	1- 500	5	250	1250	5
2	500-1000	10	750	7500	15
3	1000-1500	30	1250	37500	45
4	1500-2000	40	1750	70000	85
5	2000-2500	15	2250	33750	100
Итого		100		150000

1). Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Выбор средней определяется экономическим содержанием показателя и исходных данных. В данной задаче в каждую группу объединены одинаковые варианты, т.е. варианты имеют различный вес, поэтому вычисляется средняя арифметическая взвешенная:

_

X=Σxi fi / Σfi

_

Получаем X = 150000/100 = 1500 (руб.)

2. Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту. Моду находим по формуле:

fM₀ – fM₀-1

M₀ =XM₀ + hM₀ ----------------------------

(fM₀ – fM₀-1)+( fM₀ – fM₀+1)

где: XM₀ – минимальная граница модального интервала;

hM₀ - величина модального интервала;

fM₀, fM₀-1, fM₀+1 – частоты модального интервала, предшествующего и следующего за ним.

M₀ = 1500+500 *(40-30/ (40-30)+(40-15)) =1643

Отразим нахождение моды на графике (рисунок № 1)

Рисунок № 1. Нахождение моды.

Медиана – варианта, находящаяся в середине ряда распределения. Медиану находим по формуле:

0,5*f –S(-1)

Mе =XMе + hMе ----------------------------

fMе

где: XMе - нижняя граница медианного интервала;

hMе - величина медианного интервала;

0,5*f - полусумма частот ряда;

S(-1) - сумма накопленных частот, предшествующих медианному интервалу;

fMе - частота медианного интервала.

Mе = 1000+500*(0.5*100-15/ 30) =1583

Отразим нахождение медианы на графике (рисунок № 2)

Рисунок № 2. Нахождение медианы.

4. Коэффициент вариации

σ

V = ----*100 %

X

Показатель вариации отражает тенденцию развития явления, т.e. действие главных факторов. Показатель вариации выражается в процентах. Для расчетов необходимо найти среднее квадратическое отклонение.

∑ (Xi-X) ²fi

σ=√ --------------- - взвешенное;

∑ fi

26245000

σ=√ --------------- =512.3

100

512.3

V = -------*100 %= 34.2 %

1500

Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. В данном примере можно сделать вывод, что совокупность не является однородной.

Имеются следующие данные о распределении общего объема денежных доходов населения РФ:

Таблица № 7. Распределение общего объема денежных доходов населения

	2000 год	2001 год
Денежные доходы–всего, %	100	100
В том числе по 20-процентным группам населения:
Первая (с наименьшими доходами)	6,0	5,9
Вторая	10,4	10,4
Третья	14,8	15,0
Четвертая	21,2	21,7
Пятая (с наибольшими доходами)	47,6	47,0
Коэффициент Джини (индекс концентрации доходов)

Строим расчетную таблицу:

Таблица № 8. Итоговая

Год	Социальная группа населения	Доля населения, xi	Доля в общем объеме денежных доходов, yi	Расчетные показатели
				cum yi (S)	xiyi	Xicum yi (S)
А	1	2	3	4	5	6
2000 (базисный)	1	0,2	0,06	0,060	0,0120	0,0120
	2	0,2	0,104	0,164	0,0208	0,0328
	3	0,2	0,148	0,312	0,0296	0,0624
	4	0,2	0,212	0,524	0,0424	0,1048
	5	0,2	0,476	1,0	0,0952	0,2000
	Итого	1,0	1,0	-	0,2	0,4120
2001(отчетный)	1	0,2	0,059	0,059	0,0118	0,0118
	2	0,2	0,104	0,163	0,0208	0,0326
	3	0,2	0,150	0,313	0,0300	0,0626
	4	0,2	0,217	0,530	0,0434	0,1060
	5	0,2	0,470	1,0	0,0940	0,2000
	Итого	1,0	1,0	-	0,2	0,4130

Рассчитываем коэффициент концентрации доходов Джини по формуле: n n

G=1-2∑x_icum y_i+∑x_iy_i

i=1 i=1

для 2000 года (базисного): G = 1 – 2 * 0,4120 + 0,2 = 0,376

для 2001 года (отчетного): G = 1 – 2* 0,4130 + 0,2 = 0,374

Уменьшение коэффициента Джини до 0,374 в отчетном году с 0,376 в базисном свидетельствует об ослаблении дифференциации доходов населения РФ. Наиболее обеспеченная группа населения сконцентрировала в отчетном году 47,0% доходов против 47.6 в базисном; доля наименее обеспеченной группы сократилась до 5,9 в отчетном году против 6,0 в базисном.

Построим кривую Лоренца для каждого года (рисунок № 3)

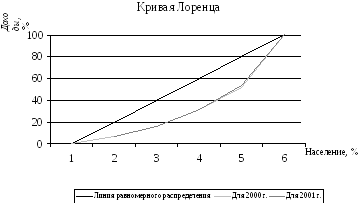
Рисунок № 3. Кривая Лоренца.

Заключение.

Социальная статистика занимается всесторонним и глубоким изучением состояния и развития экономики страны, различных социальных процессов, происходящих в ней, их закономерностей, путем сбора, обработки, анализа и обобщения данных о них. На современном этапе рыночных отношений можно выделить такие основные задачи: на базе современной системы статистических показателей, методологии их расчета и методов сбора статистической отчетности завершить создание модели государственной статистики, адаптированной к условиям развития рыночных отношений; усилить интегрирующие функции органов государственной статистики в общем процессе информационного отображения общественных явлений в стране; сформировать единую методологическую основу для отраслевых систем статистической информации; обеспечить высокую оперативность и максимальную достоверность статистических данных; повысить программно-технологический и технический уровень системы.

Показатели, изучаемые в данной отрасли, используются в изучении мероприятий по социальной защите населения России, в том числе, индексации доходов населения. При этом устанавливается порог повышения индекса цен по фиксированному набору товаров и услуг, который и служит своеобразным сигналом корректировки доходов.

Литература.

1. В.М. Гусаров. Теория статистики: М.: «Аудит», издательское объединение «ЮНИТИ», 1998.

2. Сабирьянова К. Микроэкономический анализ динамических изменений на Российском рынке труда. Вопросы экономики, N 1, 1998.

3. Лапунина Л., Четверина Т. Напряженность на Российском рынке и механизмы ее преодоления: Вопросы экономики, N 2, 1998.

4. Практикум по статистике: Учебное пособие для вузов/ под редакцией В.М. Симчеры/ ВЗФЭИ.-М.: ЗАО «Финстатинформ», 1999.

5. Российский статистический ежегодник 2002. Госкомстат

6. Социальная статистика: Учебник/ Под ред. чл.-кор. РАН И.И. Елисеевой.- 3-е изд., перераб. и доп.- М.: Финансы и статистика, 2002.- 480 с.: ил.

7. Общая теория статистики: статистическая методология в изучении коммерческой деятельности, Учебник / под редакцией А.А. Спирина, О.Э. Башиной: М.: «Финансы и статистика», , 1994.

8. Курс социально - экономической статистики. Учебник / под редакцией М.Г. Назарова: М.: ЗАО «Финстатинформ», «Юнити», 2000.

9. Интернет ресурс: www.superbroker.ru

(Дополнение к работе!)

Корреляционно-регрессионный анализ.

Корреляционно-регрессионный метод исследования состоит их двух этапов. К первому этапу относится корреляционный анализ, а к второму регрессионный.

Корреляционный анализ имеет своей задачей количественное определение тесноты связей между двумя признаками при парной связи между результативным и множеством факторных признаков при многофакторной связи.

Регрессионный анализ заключается в определении аналитического выражения связи, в которой изменение одной величины (результативного признака) обусловлена влиянием одной или нескольких независимых величин (факторов). Такая зависимость выражается уравнением прямой: y= a₀+a₁x,

где y –индивидуальное значение результативного признака,

X - индивидуальное значение факторного признака,

a₀ и a₁ –параметры равнения регрессии.

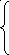na₀ + a₁ ∑x=∑y,

a₀ ∑x + a₁ ∑x² = ∑xy

Исследуем данные обследования бюджетов домашних хозяйств. Результативным признаком будет являться число домохозяйств, а факторным - среднедушевой доход. Для определения тесноты связи между изучаемыми признаками вычисляем коэффициент корреляции.

Имеются данные обследования бюджетов домашних хозяйств района:

Группы домашних хозяйств	Среднедушевой доход, руб.Y	Число домохозяйств, X	XY	X2	Y2
1	250	5	1250	25	62500
2	750	10	7500	100	562500
3	1250	30	37500	900	1562500
4	1750	40	70000	1600	3062500
5	2250	15	33750	225	5062500
Сумма	6250	100	150000	2850	10312500

Формула для определения коэффициента корреляции:

∑xy - ∑x∑y / n

R=------------------------------------------------------------------------------

√ [∑x² – (∑x)² / n] [∑y² – (∑y)² / n]

150000 – 6250*100 / 5 25000

R =------------------------------------------------------------------------------------------------------=------------------------= 0.5

√ [2850-10000 / 5] [10312500- 39062500 / 5] 46097.72