
- •Тема 1. Вступ. Дійсні числа
- •1. Вступ
- •2. Елементи теорії множин
- •Поняття відображення або функції.
- •1. Поняття відображення або функції
- •2. Потужність множин
- •3. Зчисленні множини
- •4. Математична індукція
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом .
- •Тема 2. Числові послідовності
- •1. Означення числової послідовності
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і .
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази.
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •4. Теорема про вкладені відрізки.
- •1. Теорема про вкладені відрізки.
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності.
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Тема 3. Границя функції однієї змінної
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Тема 4. Неперервні та рівномірно неперервні функції
- •1. Неперервність функції в точці
- •2. Операції над неперервними функціями
- •Розриви першого роду. Якщо в точці функція має скінченну ліву й скінченну праву границю і вони рівні між собою, тобто
- •Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
1. Збіжні послідовності
Границя числової послідовності. Число називається границею послідовності , якщо для будь-якого числа існує такий номер , що для всіх членів послідовності із номером виконується нерівність
![]() .
(2)
.
(2)
Якщо число є границею послідовності , то пишуть
![]() ,
,
а саму послідовність називають збіжною.
Послідовність, яка не є збіжною, називається розбіжною.
Приклад. Довести, що
![]()
![]() .
.
Доведення. Задамо довільне число
і покажемо, що існує таке
натуральне число
,
що для всіх членів послідовності
із номером
виконується нерівність
![]() .
.
Оскільки
![]() ,
то
,
то
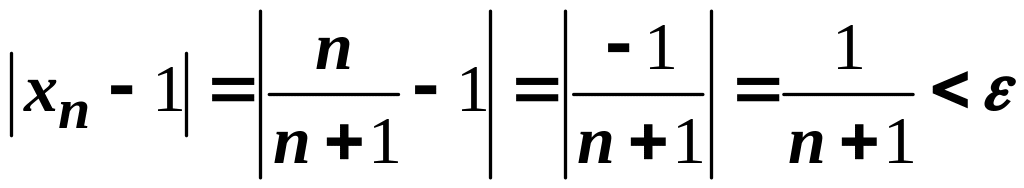 .
.
Розв'язавши відносно
нерівність
![]() ,
маємо
,
маємо
![]() .
.
Якщо в значенні
узяти цілу частину числа
![]() ,
тобто покласти
,
тобто покласти
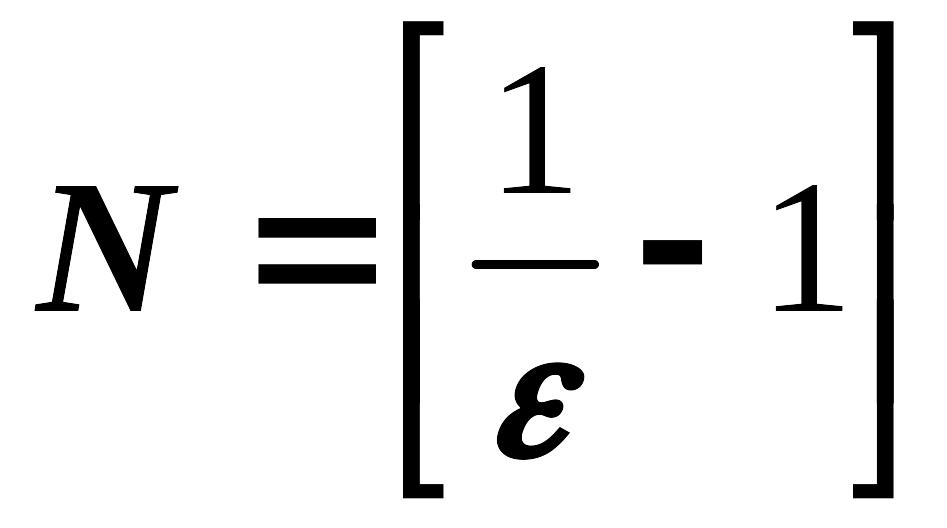 ,
то нерівність
,
то нерівність
![]() <ε
виконується для всіх
.
Отже,
<ε
виконується для всіх
.
Отже,
![]() .
.
Якщо послідовність
збіжна і
![]() ,
то будь-який її елемент
можна подати у вигляді
,
то будь-який її елемент
можна подати у вигляді
![]() ,
де
,
де
![]() -
елемент нескінченно малої послідовності
-
елемент нескінченно малої послідовності
![]() .
.
Дійсно, якщо
,
то послідовність
![]() є нескінченно малою, оскільки для
будь-якого
існує такий номер
,
що для
виконується нерівність
є нескінченно малою, оскільки для
будь-якого
існує такий номер
,
що для
виконується нерівність
![]() ,
тобто
.
,
тобто
.
Має місце й обернене твердження. Якщо
![]() можна подати у вигляді
можна подати у вигляді
![]() ,
де
нескінченно мала послідовність,
то
.
,
де
нескінченно мала послідовність,
то
.
Нерівність (2) рівносильна нерівності
![]() або
або
![]() ,
,
із якої випливає, що знаходиться в околі точки . Отже, означення границі числової послідовності можна дати наступним чином.
Число називається границею послідовності , якщо для будь-якого числа існує такий номер , що всі члени послідовності із номером знаходяться в околі точки .
Очевидно, що нескінченно велика послідовність не має границі. Іноді говорять, що вона має нескінченну границю і пишуть
![]() .
.
Якщо
при цьому, починаючи з деякого номера,
всі члени послідовності додатні (
від'ємні ), то пишуть
![]() .
.
Усяка нескінченно мала послідовність
збіжна, причому
![]() .
.
Це безпосередньо випливає з означення границі числової послідовності й означення нескінченно малої числової послідовності.
2. Властивості збіжних послідовностей
Теорема Збіжна послідовність має єдину границю.
Доведення.
Припустимо, що збіжна послідовність
![]() має дві різні границі
і
має дві різні границі
і
![]() ,
тобто
,
тобто
![]() .
Тоді
та
.
Тоді
та
![]() ,
де
,
де
![]() і
і
![]() елементи нескінченно
малих послідовностей
та
елементи нескінченно
малих послідовностей
та
![]() .
Отже,
.
Отже,
![]() або
або
![]() Оскільки
Оскільки![]() ,
за властивістю нескінченно малих
послідовностей, є елементами нескінченно
малої послідовності, а
,
за властивістю нескінченно малих
послідовностей, є елементами нескінченно
малої послідовності, а
![]() постійне число, то
постійне число, то
![]() .
Таким чином,
.
.
Таким чином,
.
Теорема. Якщо послідовність збіжна, то вона обмежена.
Доведення. Нехай і - номер, починаючи з якого виконується нерівність , де . Тоді
![]()
для всіх
.
Виберемо
![]() .
За цієї умови
для будь-якого
.
За цієї умови
для будь-якого
![]() .
.
Зазначимо,
що не всяка обмежена послідовність є
збіжною. Наприклад, послідовність
![]() обмежена, але не збіжна.
обмежена, але не збіжна.
Теорема 2.6. Якщо і збіжні послідовності, то:
Послідовність
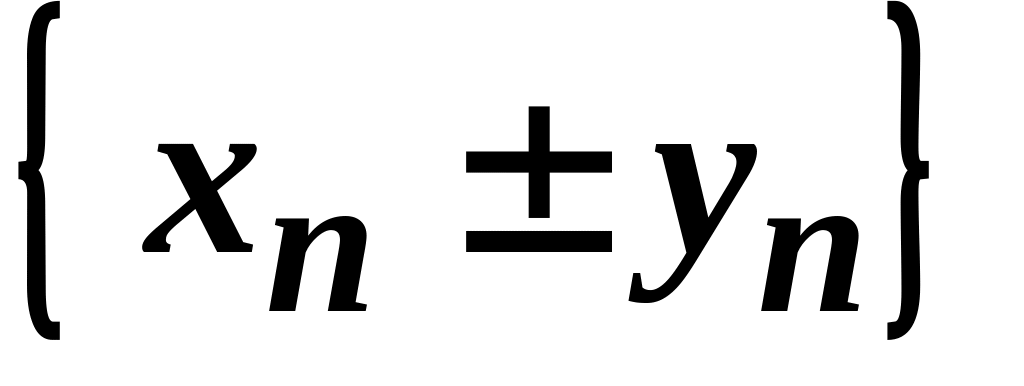 ,
яка є сумою (різницею) збіжних
послідовностей
та
,
збіжна і її границя дорівнює сумі
(різниці) границь цих послідовностей,
тобто
,
яка є сумою (різницею) збіжних
послідовностей
та
,
збіжна і її границя дорівнює сумі
(різниці) границь цих послідовностей,
тобто
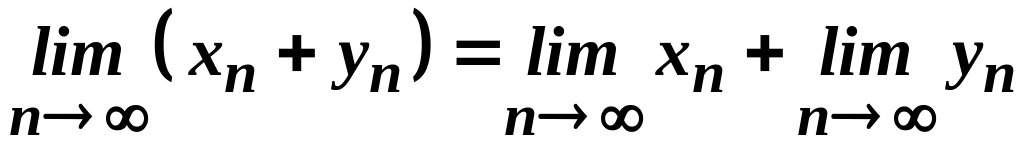 .
.
Послідовність , яка є добутком збіжних послідовностей й , збіжна і її границя дорівнює добутку границь цих послідовностей, тобто
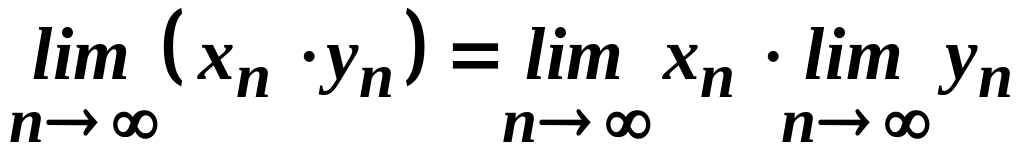 .
.Послідовність , яка є часткою збіжних послідовностей та , за умови
 , збіжна і її границя дорівнює частці
границь цих послідовностей, тобто
, збіжна і її границя дорівнює частці
границь цих послідовностей, тобто
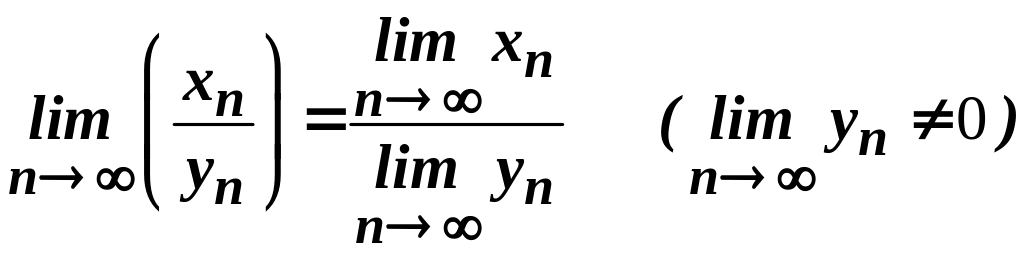 .
.
Доведення. Нехай
і
збіжні послідовності
та
![]() .
Тоді
і
.
Тоді
і
![]() ,
де
й
–
елементи нескінченно малих послідовностей
і
.
Покажемо, що має місце:
,
де
й
–
елементи нескінченно малих послідовностей
і
.
Покажемо, що має місце:
1)
![]() .
.
Оскільки
![]() є елементами нескінченно малої
послідовності
є елементами нескінченно малої
послідовності
![]() ,
то звідси випливає, що
.
,
то звідси випливає, що
.
2)
![]() .
.
Оскільки
![]() є елементами нескінченно малої
послідовності
є елементами нескінченно малої
послідовності
![]() ,
то
,
то
![]() .
.
Тобто .
3)
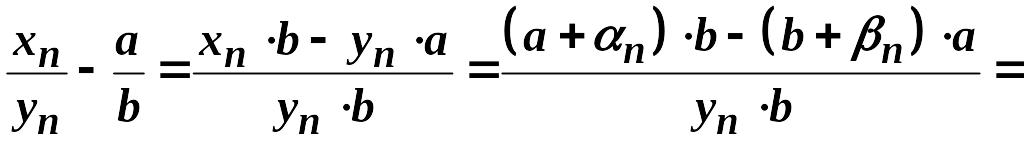
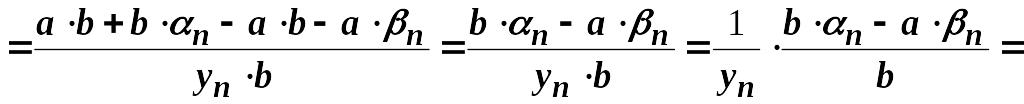
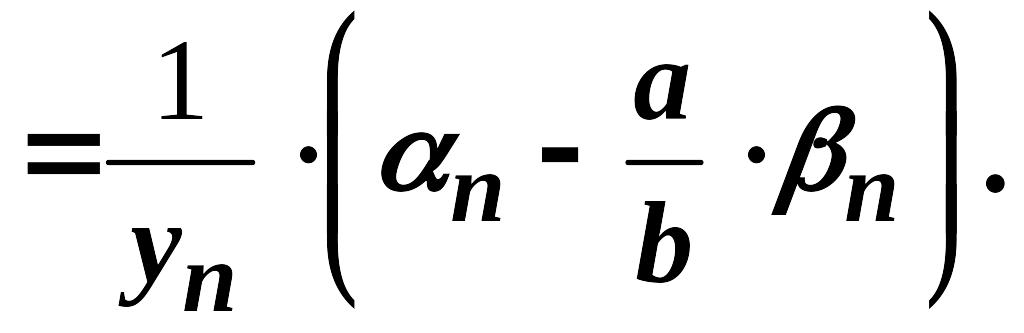
Послідовність
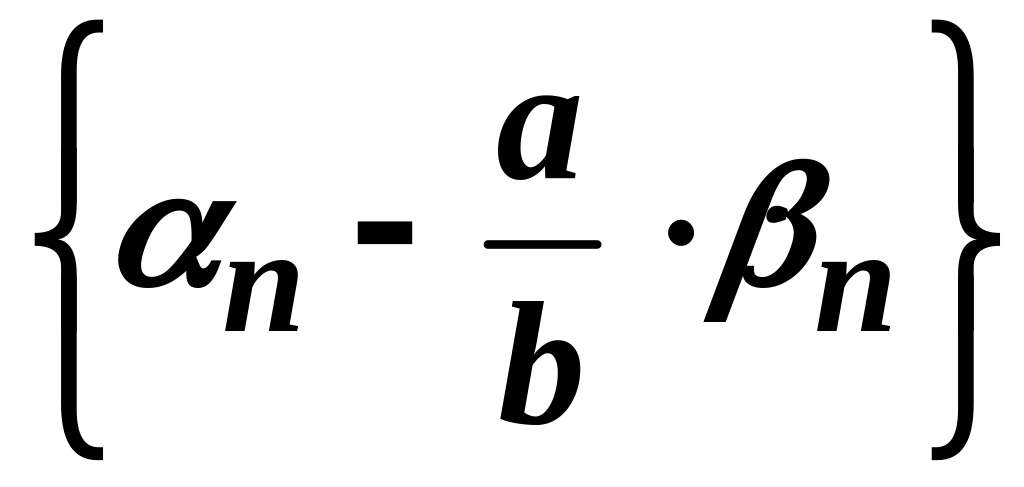 є нескінченно малою. Покажемо, що
послідовність
є нескінченно малою. Покажемо, що
послідовність
![]() обмежена. Оскільки
обмежена. Оскільки
![]() і
і
![]() ,
то для
,
то для
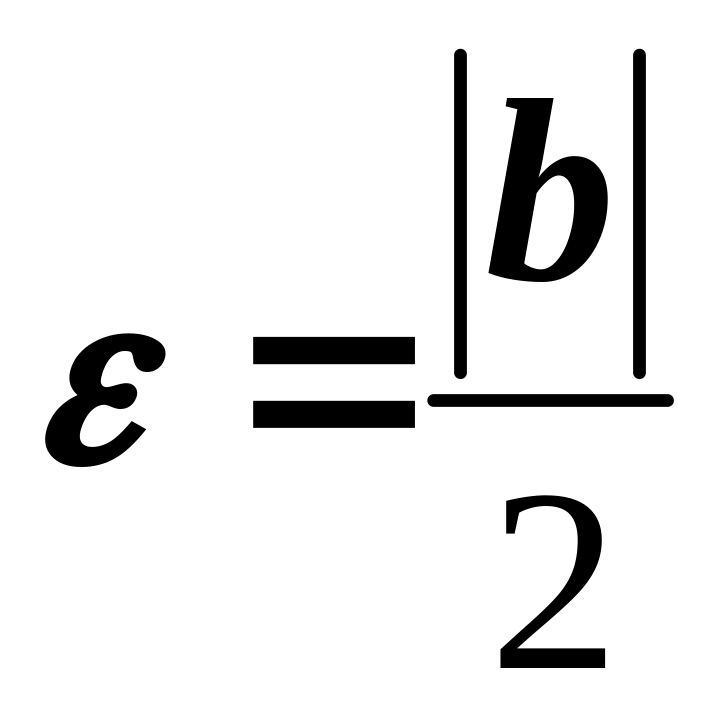 існує такий номер
,
що для всіх
виконується нерівність
існує такий номер
,
що для всіх
виконується нерівність
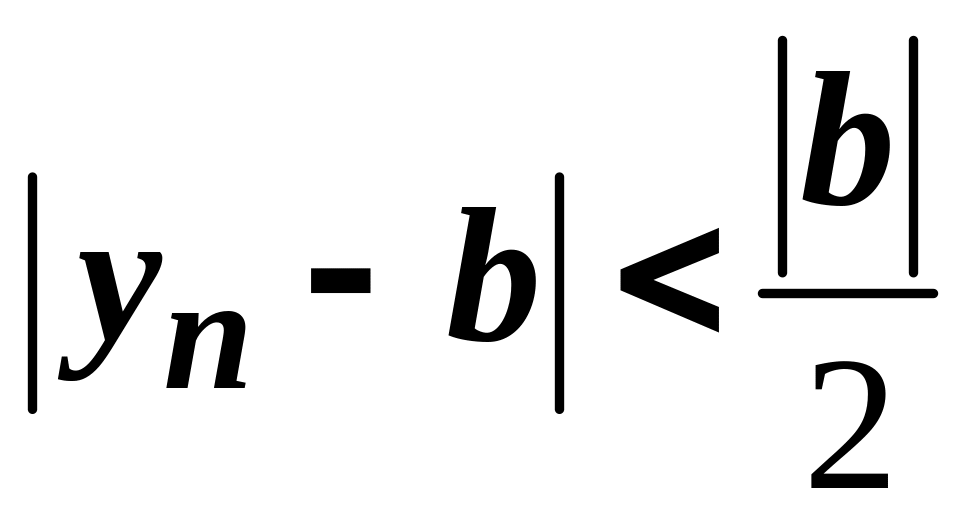 ,
,
отже,
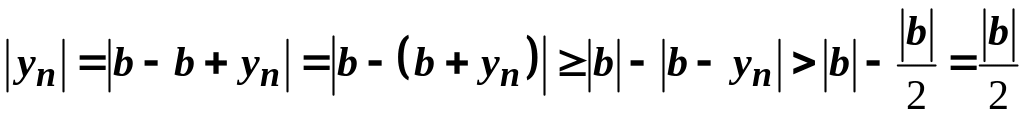 ,
тобто
,
тобто
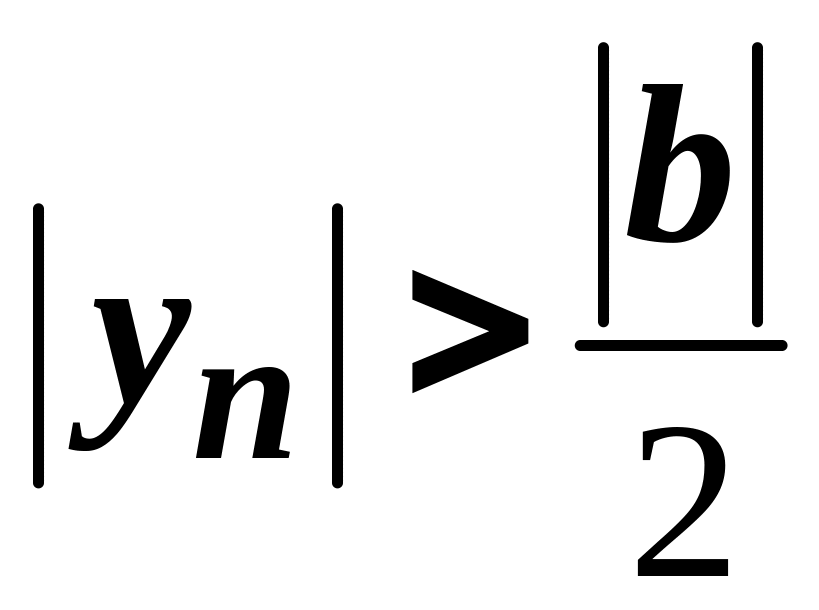 ,
а тому
,
а тому
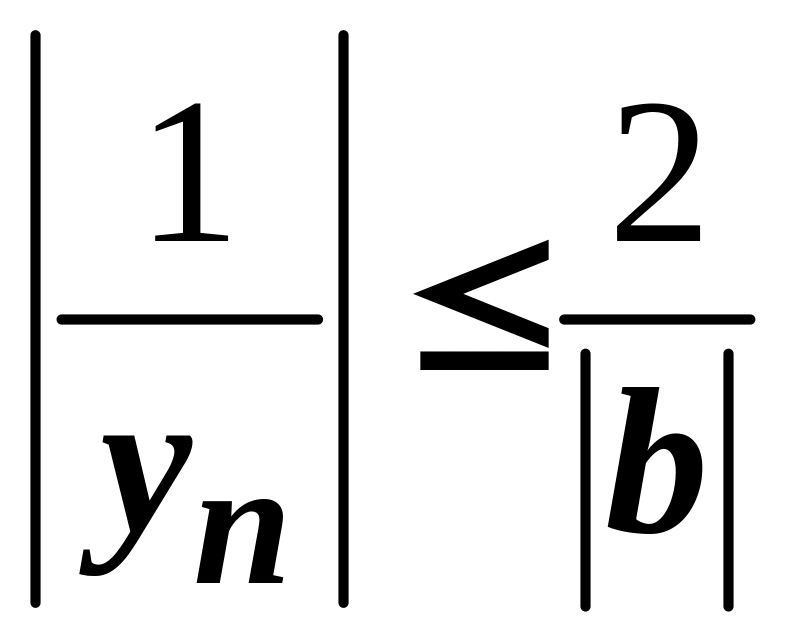 для всіх
.
Звідси випливає, що послідовність
обмежена.
для всіх
.
Звідси випливає, що послідовність
обмежена.
Таким чином, послідовність нескінченно мала, а тому
 ,
,
тобто
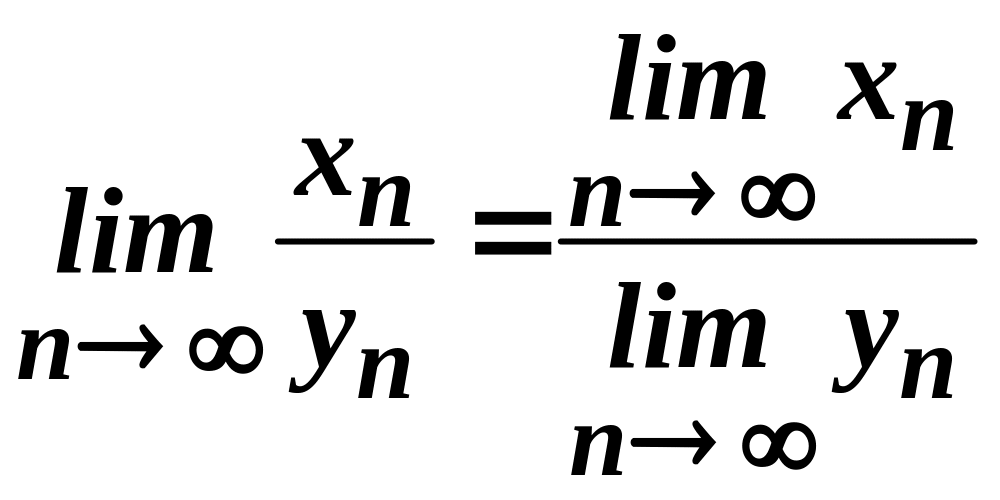 ,
де
.
,
де
.
Зауваження. Пункт 1) наведеної теореми допускає узагальнення на довільне скінченне число доданків. Пункт 2) - на довільне скінченне число множників. Із пункту 2) випливає, що постійний множник можна виносити за знак границі, тобто
![]() .
.
