
- •Тема 1. Вступ. Дійсні числа
- •1. Вступ
- •2. Елементи теорії множин
- •Поняття відображення або функції.
- •1. Поняття відображення або функції
- •2. Потужність множин
- •3. Зчисленні множини
- •4. Математична індукція
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом .
- •Тема 2. Числові послідовності
- •1. Означення числової послідовності
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і .
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази.
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •4. Теорема про вкладені відрізки.
- •1. Теорема про вкладені відрізки.
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності.
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Тема 3. Границя функції однієї змінної
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Тема 4. Неперервні та рівномірно неперервні функції
- •1. Неперервність функції в точці
- •2. Операції над неперервними функціями
- •Розриви першого роду. Якщо в точці функція має скінченну ліву й скінченну праву границю і вони рівні між собою, тобто
- •Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Нескінченно малі і нескінченно великі послідовності.
Послідовність
називається нескінченно великою,
якщо для будь-якого числа
існує такий номер
![]() ,
що для всіх елементів
із номером
,
що для всіх елементів
із номером
![]() виконується нерівність
.
виконується нерівність
.
Зауваження.
У наведеному означенні номер
залежить від числа
,
тобто
![]() .
.
Очевидно,
що всяка нескінченно велика послідовність
є необмеженою, проте не всяка необмежена
послідовність є нескінченно великою.
Наприклад, необмежена послідовність
0, 1, 0, 2, 0, 3, ..., n,
0, n+1,
… не є нескінченно
великою, оскільки не існує такого номера
,
щоб для всіх
,
де
виконувалася б, наприклад, нерівність
![]() .
.
Послідовність
![]() називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа
існує такий номер
,
що для всіх елементів
із номером
виконується нерівність
називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа
існує такий номер
,
що для всіх елементів
із номером
виконується нерівність
![]() .
.
Зауваження.
У наведеному означенні номер
залежить від числа
,
тобто
![]() .
.
Приклад
1. Показати, що послідовність
![]() є нескінченно великою.
є нескінченно великою.
Нехай
маємо довільне число
.
Із нерівності
![]() або
або
![]() .
.
Покладемо
![]() .
.
Тоді
![]() .
Оскільки
.
Оскільки
![]() ,
то
,
то
![]() .
Отже, при
виконується нерівність
.
.
Отже, при
виконується нерівність
.
Приклад
2. Показати, що послідовність
![]() є нескінченно малою.
є нескінченно малою.
Нехай
маємо довільне число
.
Із нерівності
 одержуємо
одержуємо
 .
Покладемо
.
Покладемо
 .
Тоді для всіх
маємо
.
Тоді для всіх
маємо
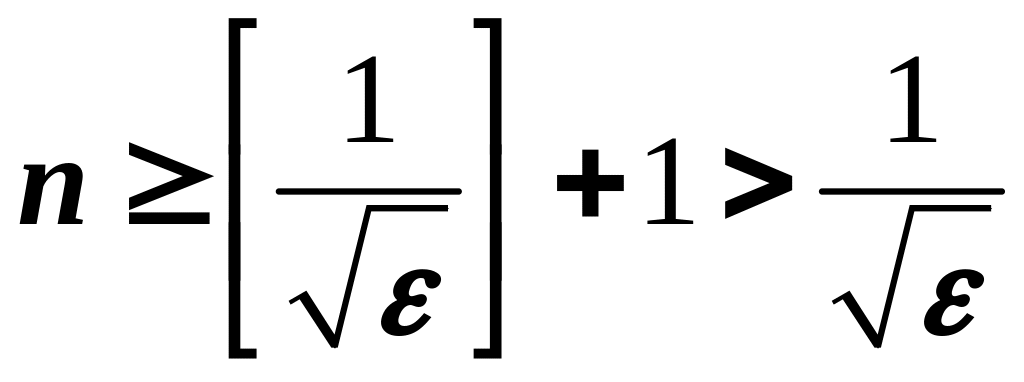 ,
тобто
,
тобто
![]() або
або
 .
.
Теорема.
Якщо
нескінченно велика
послідовність і всі її члени відмінні
від нуля, то послідовність
![]() нескінченно мала, і, навпаки, якщо
нескінченно мала
послідовність й
нескінченно мала, і, навпаки, якщо
нескінченно мала
послідовність й
![]() ,
то послідовність
,
то послідовність
![]() нескінченно велика.
нескінченно велика.
Доведення. Нехай
нескінченно велика
послідовність. Візьмемо довільне
і покладемо
![]() .
Оскільки
нескінченно велика послідовність, то
для вказаного
існує номер
такий, що при
виконується нерівність
.
Звідси маємо
.
Оскільки
нескінченно велика послідовність, то
для вказаного
існує номер
такий, що при
виконується нерівність
.
Звідси маємо
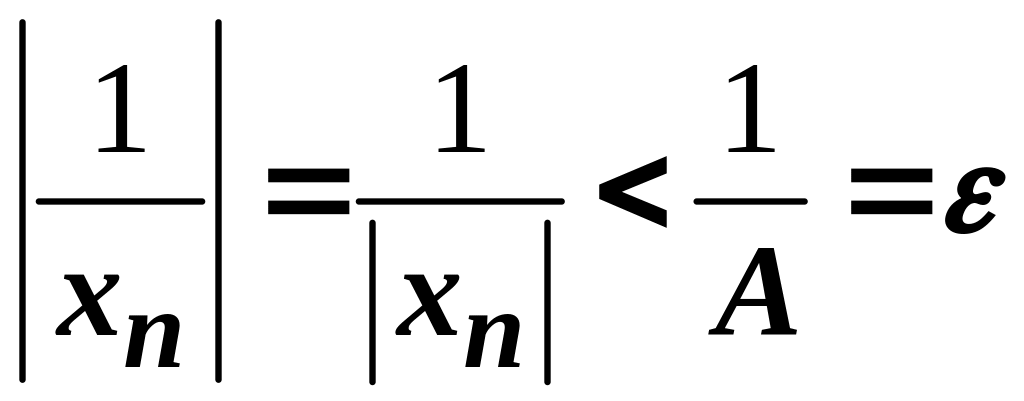 .
Отже, послідовність
.
Отже, послідовність
![]() нескінченно мала.
нескінченно мала.
Друга частина теореми доводиться аналогічно.
5. Основні властивості нескінченно малих послідовностей
Теорема. Сума (різниця) двох нескінченно малих послідовностей є нескінченно малою послідовністю.
Доведення.
Нехай
і
![]() нескінченно малі
послідовності. Задамо довільне
.
Тоді існує такий номер
нескінченно малі
послідовності. Задамо довільне
.
Тоді існує такий номер
![]() ,
що при
,
що при
![]() ,
й існує такий номер
,
й існує такий номер
![]() ,
що при
,
що при
![]() .
Виберемо
.
Виберемо
![]() .
Тоді при
виконуватимуться нерівності
.
Тоді при
виконуватимуться нерівності
![]() і
і
![]() .
Отже, при
.
Отже, при
![]() .
.
Звідси випливає, що
послідовності
![]() і
і
![]() нескінченно малі.
нескінченно малі.
Наслідок. Алгебраїчна сума будь-якого скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.
Теорема. Добуток обмеженої послідовності на нескінченно малу є нескінченно малою послідовністю.
Доведення.
Нехай
обмежена послідовність,
а
нескінченно мала.
Оскільки
обмежена, то існує таке число
,
що для всіх
виконується нерівність
![]() .
Задамо довільне
.
Оскільки послідовність
нескінченно мала, то існує такий номер
,
що при
виконується нерівність
.
Задамо довільне
.
Оскільки послідовність
нескінченно мала, то існує такий номер
,
що при
виконується нерівність
![]() .
Отже, при
.
Отже, при
![]() .
.
Звідси
випливає, що послідовність
![]() нескінченно мала.
нескінченно мала.
Наслідок 1. Добуток нескінченно малої послідовності на число є нескінченно малою послідовністю.
Наслідок 2. Добуток двох нескінченно малих послідовностей є нескінченно малою послідовністю.
Дійсно, якщо послідовність нескінченно мала, то вона обмежена. Отже, добуток двох нескінченно малих послідовностей можна розглядати як добуток нескінченно малої послідовності на обмежену.
Із наслідку 2 випливає, що добуток скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.
Зауваження. Стосовно частки двох нескінченно малих послідовностей у загальному випадку нічого сказати не можна, оскільки вона може бути нескінченно малою, постійною, нескінченно великою послідовністю або взагалі не визначеною.
ЛЕКЦІЯ 6
Збіжні послідовності.
Властивості збіжних послідовностей.
Невизначені вирази.
