Лекция№3 (ИУ для всех)

1. Способы преобразования

Частные положения фигур относительно плоскостей проекций более удобны для решения геометрических задач в первую очередь метрических задач (определение длины, угла, площади).

Можно отметить два пути решения задачи изменения положения фигуры относительно плоскостей проекций:

1. изменить положение плоскостей проекций, не изменяя положения фигуры;

2. изменить положение фигуры, не меняя положения плоскостей проекций.

Способ замены плоскостей проекций

Условия преобразования:

1. положение фигуры неизменно;

2. изменяется положение одной из двух плоскостей проекций;

3. новую плоскость проекций располагают перпендикулярно оставшейся плоскости проекций (рис 1).

Рис. 1

4. Положение новой плоскости проекций может быть задано или выбрано.

Построение профильной проекции точки (фигуры) есть также использование способа замены плоскостей проекций (рис. 2)

Рис. 2

Метрические задачи, решаемые способом замены плоскостей проекций:

Примеры задач.

Задача 1. Определить длину отрезка (рис. 3)

Задача 2. Преобразовать прямую общего положения в проецирующую (см. рис. 37)

Первая замена

z = const

Вторая замена

y = const

Рис. 3

Задача 3. Преобразовать плоскость общего положения в проецирующую.

Определить угол наклона плоскости к горизонтальной плоскости проекций (рис. 4).

Задача 4. . Преобразовать плоскость общего положения в плоскость уровня (см. рис. 38).

О пределить истинный вид плоскости ∆ ABC.

Рис. 4

Способ вращения вокруг проецирующей прямой – частный случай плоско-параллельного перемещения.

Условия преобразования:

1. ось вращения i неподвижна и перпендикулярна плоскости проекций;

2. все точки фигуры перемещаются по окружностям, плоскости которых перпендикулярны оси i (рис.5);

3. точки лежащие на оси вращения i неподвижны (см. рис. 5)

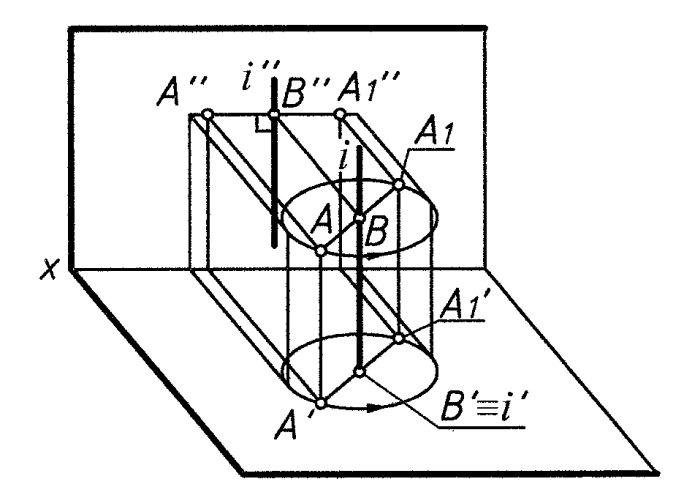
Рис. 5

Пример задачи:

О пределить длину отрезка вращением вокруг проецирующей прямой (рис. 6)

Рис. 6

Пересечение тел проецирующей плоскостью Пересечение многогранников плоскостью

На рис. 7 призма усечена плоскостью γ, наклоненной под углом α° к оси призмы и перпендикулярной фронтальной плоскости.

Секущая плоскость пересекает ребра призмы в точках К, М, М_1, N, N_1, а грани призмы – по прямым, заключенным между этими точками. Верхнее основание пересекается секущей плоскостью по прямой LL₁. Результатом пересечения является семиугольник, который проецируется:

- на фронтальную плоскость проекций – в прямую, совпадающую с проекцией плоскости γ;

- на горизонтальную плоскость – в семиугольник, пять вершин которого К', М', М₁'_, N', N₁' совпадают с вершинами шестигранника, а две оставшиеся вершины L' и L₁' принадлежат прямой, по которой плоскость γ пересекает верхнее основание призмы;

- на профильную плоскость проекций – в семиугольник, вершины которого построены с помощью горизонтальных линий связи и координат Y точек L и L₁.

На рис. 7 построен истинный вид фигуры сечения призмы плоскостью γ, на дополнительную плоскость, параллельную плоскости γ, с использованием координат Y точек К, М, М_1, N, N₁, L, L₁.

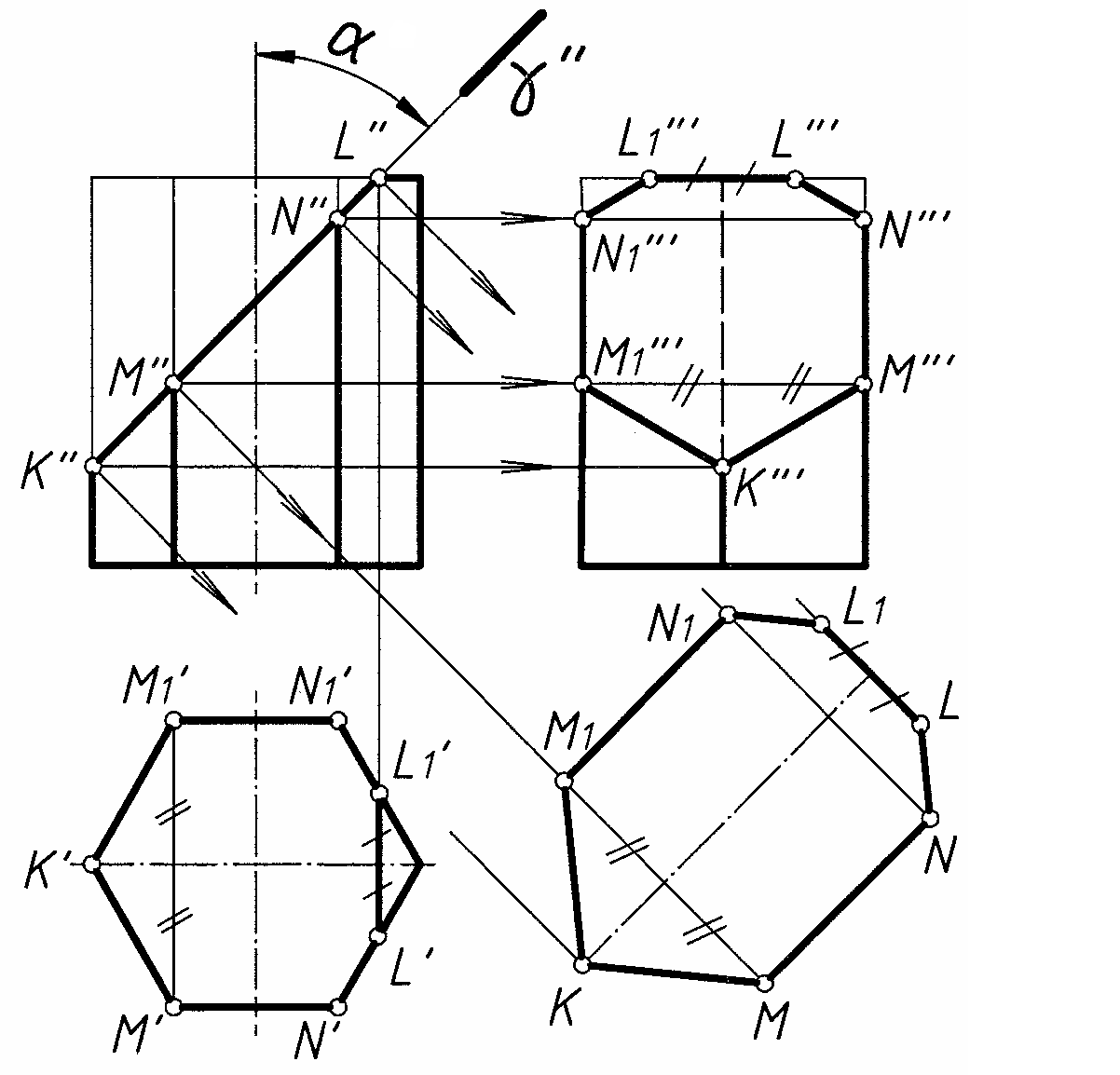
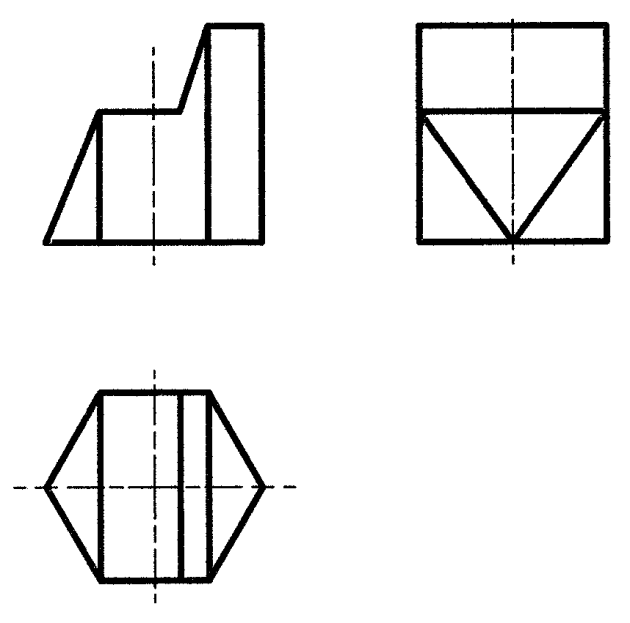
Рис. 7 Рис. 8

На рис. 8 показано пересечение правильной прямой призмы с тремя фронтально-проецирующими плоскостями.

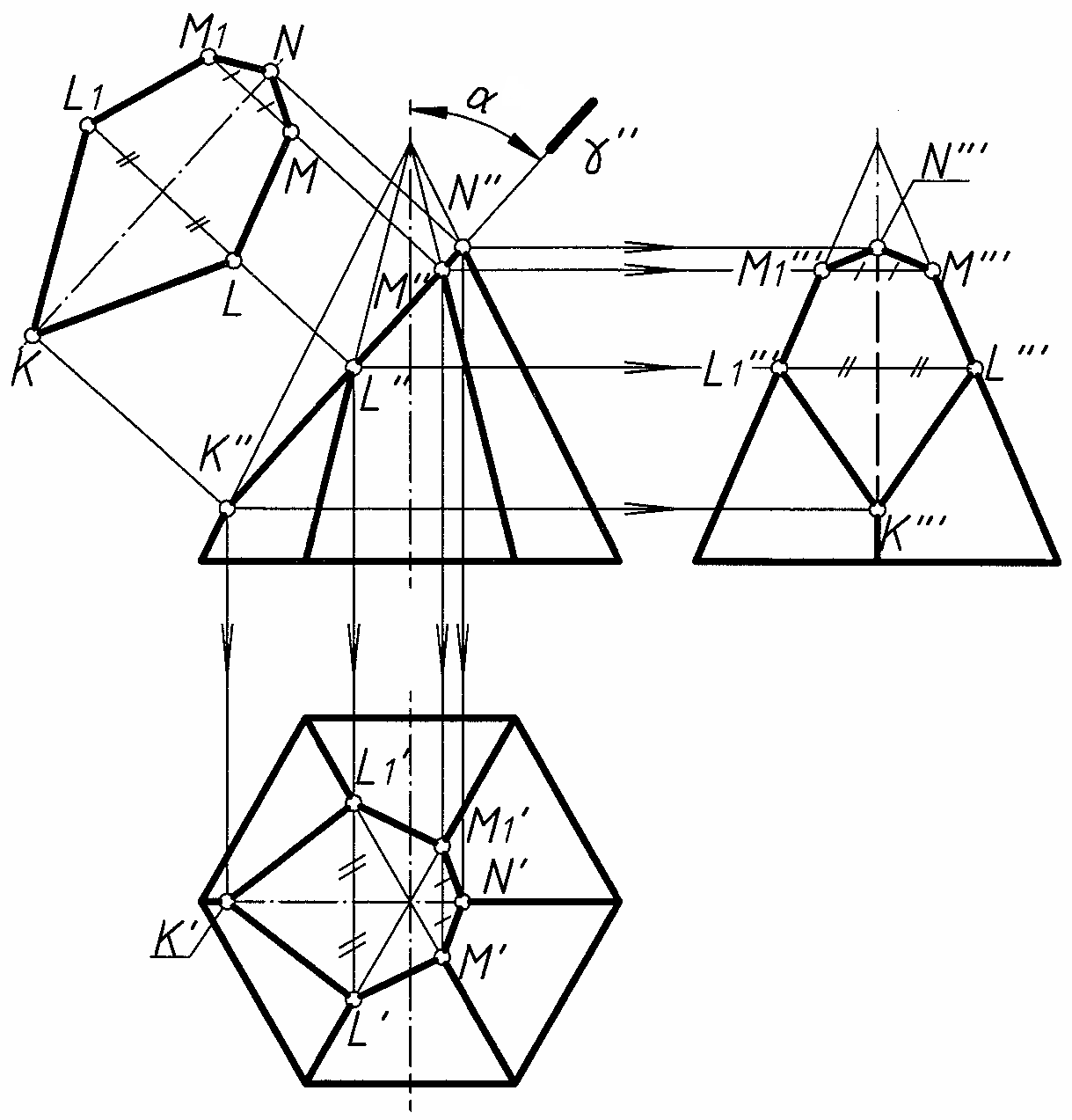
Рис. 9

На рис. 9 построены проекции пирамиды, усеченной фронтально-проецирующей плоскостью γ, наклоненной к оси пирамиды под углом α°.

Секущая плоскость пересекает ребра пирамиды в точках K,L,M,N,M₁ и L₁, а грани – по прямым, соединяющим эти точки. Результатом пересечения плоскости γ и пирамиды является шестиугольник, который проецируется:

- на фронтальную плоскость проекций в прямую, совпадающую с проекцией плоскости γ;

- на горизонтальную и профильную плоскости в шестиугольники, вершины которых лежат на соответствующих ребрах и найдены с помощью линий связи.

Помимо этого на рис. 43 построен истинный вид шестиугольника на дополнительную плоскость, параллельную плоскости γ, с использованием координат Y его вершин.

На рис. 10 построены проекции пирамиды со сквозным треугольным отверстием.

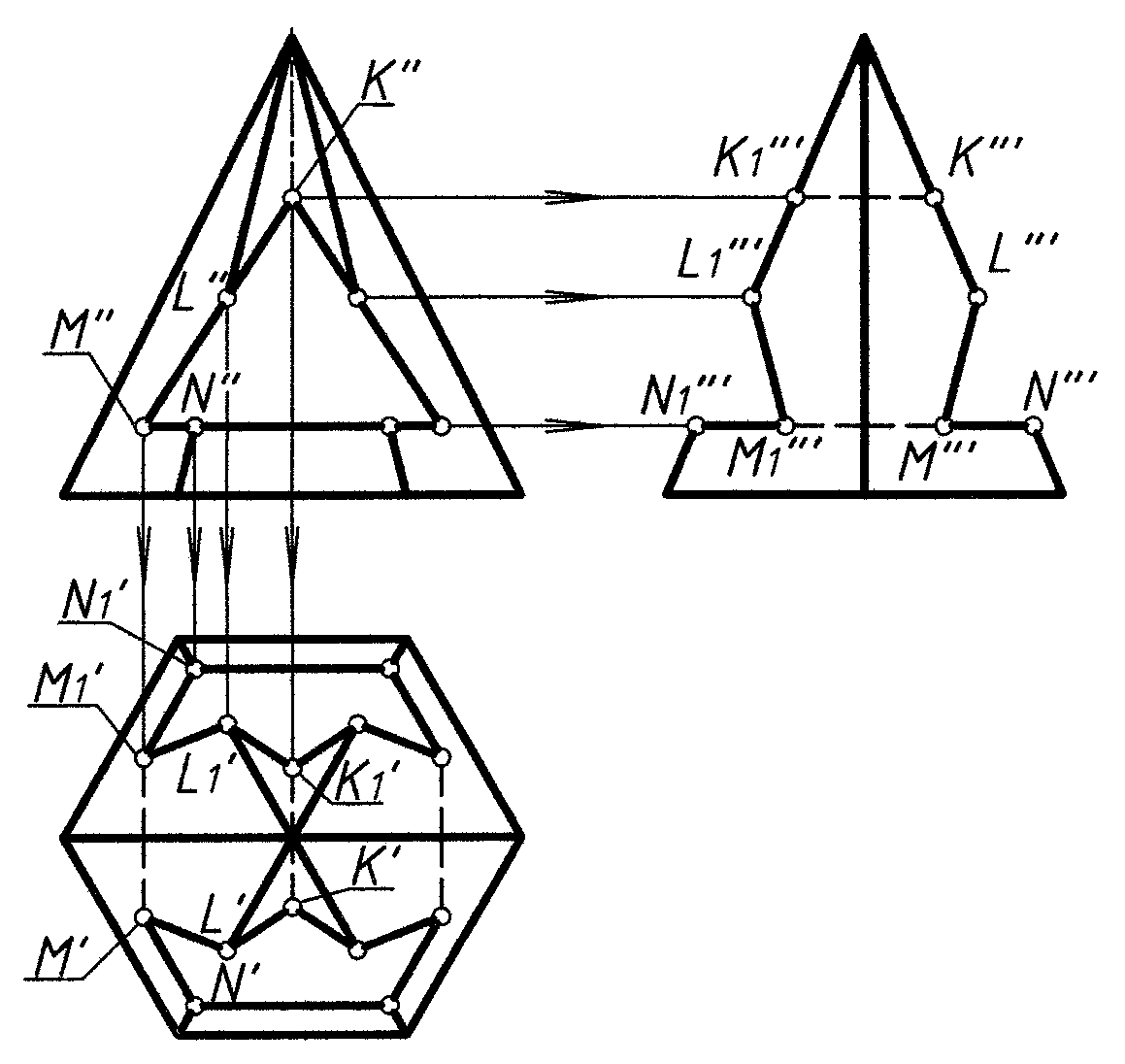
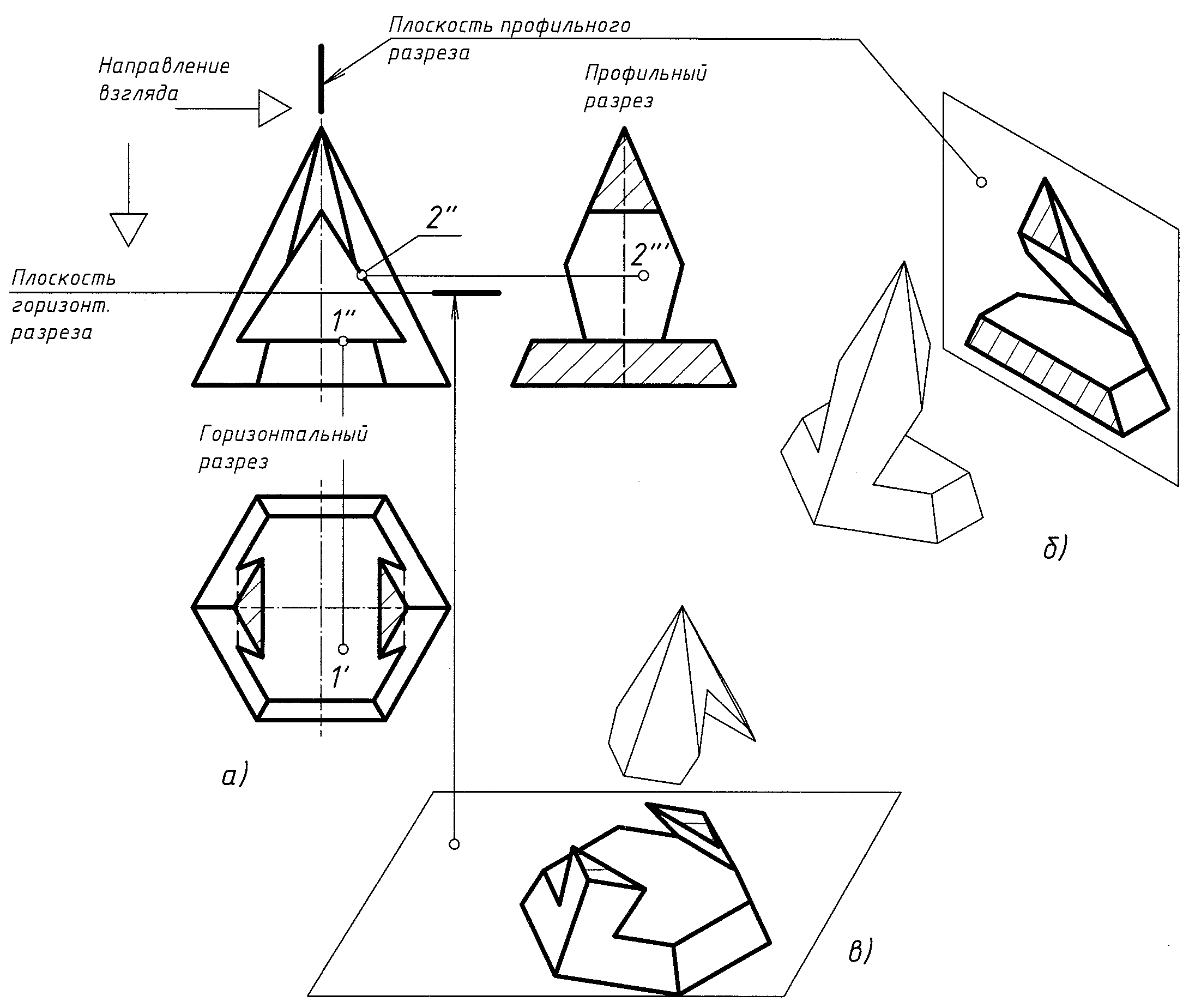
Рис. 10

Три плоскости отверстия перпендикулярны фронтальной плоскости проекций и проецируются на нее в прямые – стороны треугольника. Плоскости отверстия пересекают ребра пирамиды в точках, а грани – по прямым, соединяющим эти точки. Сквозное отверстие вырезает часть ребер и граней пирамиды, поэтому очерк фигуры на профильной плоскости проекций изменяется, приобретая вид ломаной линии. Построения завершают проведением линий невидимого контура, в которые проецируются линии пересечения плоскостей сквозного отверстия.

Для того чтобы сделать видимыми внутренние поверхности пирамиды, на рис. 10 выполнены два разреза: горизонтальной и вертикальной (профильной) плоскостями. Стрелками указано направление взгляда.

На горизонтальном разрезе (рис. 10, а) стала видимой горизонтальная плоскость сквозного отверстия. Точка 1 (1', 1") располагается на этой плоскости. Часть пирамиды, расположенную выше плоскости горизонтального разреза, мысленно удаляют. Заштрихованы треугольники, по которым плоскость горизонтального разреза разделила удаленную и оставшуюся части пирамиды.

На профильном разрезе стала видимой правая боковая плоскость отверстия (рис. 10б). Точка 2 (2', 2") принадлежит этой плоскости. Половину пирамиды, расположенную перед плоскостью профильного разреза (учесть направление взгляда), мысленно удаляют. Заштрихованы фигуры, по которым произошло разделение удаленной и оставшейся частей пирамиды. Оба разреза сделаны независимо друг от друга как для целой фигуры.

Лекция №4 (ИУ3, 8, 5, 6)