2.9 Конечный автомат

Вместо того чтобы писать программу с помощью регулярных выражений, можно использовать соответствующий конечный автомат. Конечный автомат состоит из конечного множества состояний и переходов между ними, которые определяются считываемыми знаками из входной строки. При этом одно состояние определяется как начальное, а одно или более состояний – как конечные. Конечный автомат принял входную строку, если, начав работу с начального состояния и выполнив соответствующие переходы при считывании каждого знака исходной строки, автомат переходит в конечное состояние, когда строка полностью считана.

Формально конченый автомат определяется как следующая пятерка элементов:

М = (К, , , S, F),

где К – множество состояний;  – алфавит, на основе которого формируются входные строки;  – множество переходов; S(S  К) – начальное состояние; F(F  K) – множество конечных состояний.

Переходы  можно определить как таблицу или графически. Они для каждого состояния указывают следующее состояние и все возможные входные знаки. Например, конечный автомат для распознавания идентификатора можно определить, как показано на рисунке 18, где изображено два состояния: состояние 1 (начальное) и состояние 2 (конечное). Считывание буквы в состоянии 1 приводит к переходу в состояние 2, после чего считывание любого числа цифр или букв снова приводит в состояние 2.

Рисунок 18. Конечный автомат для распознавания идентификатора

При создании распознавателей удобно использовать представление конечных автоматов.

Действительное число, определенное как регулярное выражение, можно представить с помощью конечного автомата (рисунок 19).

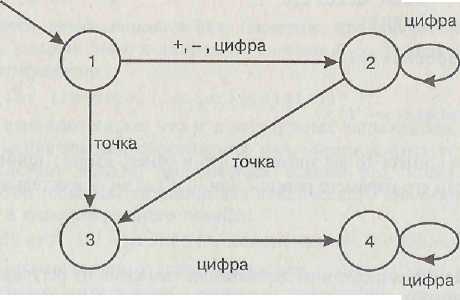
Рисунок 19. Представление действительного числа с помощью конечного автомата

Распознаватель языка – программа, которая получает на вход строку х и отвечает "да", если х – предложение языка, или в противном случае "нет". Регулярное выражение компилируется в распознаватель путем построения обобщенной диаграммы переходов, называемой конечным автоматом. Конечный автомат может быть детерминированным или недетерминированным. Недетерминированный автомат может иметь более одного перехода из состояния при одном и том же входном символе.

Конечные автоматы способны к распознаванию точных регулярных множеств. Они могут распознавать все, что могут обозначать регулярные выражения. Детерминированные конечные автоматы, которые приводят к более быстрому распознаванию, обычно больше по размеру, чем эквивалентные недетерминированные.

В приведенных ниже примерах используется в первую очередь язык, заданный регулярным выражением (а | b) * abb, состоящим из множества всех строк из а и b, которые заканчиваются на abb. Например, регулярное выражение для имен всех файлов, заканчивающихся на .о, имеет вид

( . | о | с) * .о

где с – символ, отличающийся от точки и о. Другой пример – комментарий в языке С, начинающийся с /*. Этот комментарий – последовательность символов, заканчивающаяся на */, с дополнительным требованием, чтобы ни один собственный префикс не заканчивался на */.

Недетерминированные конечные автоматы

Недетерминированный конечный автомат (НКА) – математическая модель, состоящая из:

– множества состояний S;

– множества входных символов X (символов входного алфавита);

– функции переходов move, отображающей пары символ-состояние на множество состояний;

– состояния s₀, известного как стартовое (начальное);

– множества состояний F, известных как допускающие (конечные).

НКА может использоваться в виде помеченного ориентированного графа, так называемого графа переходов, узлы которого представляют собой состояния, а помеченные дуги составляют функцию переходов. Такой граф похож на диаграмму переходов, однако один и тот же символ может помечать два и более переходов из одного состояния, а некоторые переходы могут быть помечены специальным символом , как обычным входным символом (-переходы).

Граф переходов для НКА, распознающего язык (a|b)*abb, показан на рисунке 20.

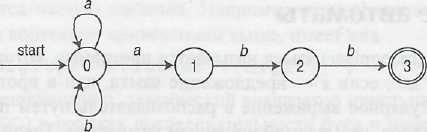
Рисунок 20. Граф переходов для НКА

Множество состояний НКА – {0, 1, 2, 3}, входной алфавит – {а, b}. Состояние 0 – стартовое, а заключительное состояние 3 представлено двойным кружком.

При описании НКА воспользуемся графом переходов. Функция переходов НКА может быть реализована различными способами. Простейший из них – таблица переходов (таблица 2), в которой строки представляют состояния, а столбцы – входные символы. Запись в строке i для символа а является множеством состояний, которые могут быть достигнуты переходом из состояния i при входном символе а.

Таблица 2. Таблица переходов для НКА

Состояние	Входной символ
	а	b
0 1 2	{0,1} – –	{0} {2} {3}

Представление автомата таблицей переходов обеспечивает быстрый доступ к переходам из данного состояния по данному символу. Вместе с тем таблица занимает много места, когда входной алфавит велик и большинство переходов ведут в пустое множество состояний. Представление функции переходов в виде списка более компактно, правда, в данном случае замедляется доступ к переходам. Каждое из этих представлений легко преобразовать в другое.

НКА принимает входную строку х, когда в графе переходов существует путь от начального состояния к какому-либо из заключительных, такой, что метки дуг этого пути соответствуют строке х. НКА на рисунке 20 допускает входные строки abb, aabb, babb, aaabb, .... Например, aabb допускается по пути из 0 вдоль дуги а в состояние 0, затем в состояния 1, 2 и 3 вдоль дуг, помеченных, соответственно, a, b и b.

Путь может быть представлен в виде последовательности переходов состояний, так называемых перемещений. В заключительное состояние может приводить более чем одна последовательность перемещений. Например, для входной строки aabb могут быть осуществлены и другие последовательности перемещений, не приводящие в заключительное состояние.

Детерминированные конечные автоматы

Детерминированный конечный автомат (ДКА) является специальным случаем недетерминированного конечного автомата, в котором:

– отсутствуют состояния, имеющие -переходы;

– для каждого состояния s и входного символа а существует не более одной дуги, исходящей из s и помеченной как а.

Детерминированный конечный автомат имеет для любого входного символа не более одного перехода из каждого состояния. Если для представления функции переходов ДКА используется таблица, то каждая запись в ней представляет собой единственное состояние. Следовательно, можно проверить, допускает ли данный ДКА некоторую строку, поскольку имеется не более одного пути от стартового состояния, помеченного этой строкой.

Алгоритм моделирования ДКА

Вход. Входная строка х, завершаемая символом конца файла eof, и ДКА D со стартовым состоянием s₀ и множеством заключительных состояний F.

Выход. "Да", если D допускает х, и "нет" в противном случае.

На рисунке 21 показан граф переходов ДКА, допускающего тот же язык (a| b) *abb, что и НКА на рисунке 20. При работе с этим ДКА и входной строкой аbаbb алгоритм пройдет последовательность состояний 0, 1, 2, 1, 2, 3 и ответит "да".

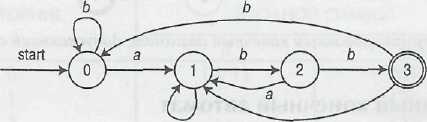
Рисунок 21. Граф переходов ДКА, допускающий строку (a | b) *аbb

Преобразование НКА в ДКА

НКА на рисунке 20 имеет два перехода из состояния 0 для входного символа а в состояние 0 или 1. Ситуация, когда можно выбрать переход для  или реально введенного символа, также неоднозначна. Ситуации, в которых функция переходов многозначна, делают моделирование НКА сложной задачей. Определение допустимости утверждает только, что должен существовать некоторый путь, помеченный входной строкой и ведущий от начального к заключительному состоянию. Однако когда имеется много путей для одной и той же входной строки, возможно, придется рассматривать их все, чтобы найти путь к заключительному состоянию или выяснить, что такого пути не существует.

Рассмотрим алгоритм для преобразования НКА в ДКА, распознающий тот же язык, что и НКА. Этот алгоритм, называемый построением подмножества, полезен при моделировании НКА.

В таблице переходов НКА каждая запись – множество состояний, а в таблице переходов ДКА – единственное состояние. Идея преобразования НКА в ДКА состоит в том, что каждое состояние ДКА соответствует множеству состояний НКА. ДКА использует свои состояния для отслеживания состояний, в которых НКА может находиться после чтения очередного входного символа. После чтения входного потока а₁а₂…а_n ДКА находится в состоянии, которое представляет подмножество Т состояний НКА, достижимых из стартового состояния НКА по пути, помеченному как а₁а₂...а_n. Количество состояний ДКА может оказаться экспоненциально зависящим от количества состояний НКА.

Построение ДКА из НКА (построение подмножества)

Вход. НКА N.

Выход. ДКА D, допускающий тот же язык.

Данный алгоритм строит таблицу переходов Dtran для D. Каждое состояние ДКА – множество состояний НКА, и Dtran строится так, чтобы D "параллельно" моделировал все возможные перемещения N по данной входной строке.

Для отслеживания множеств состояний НКА используем операции, приведенные в таблице 3, где $ представляет состояние НКА, а Т– множество состояний НКА.

Таблица 3. Операции над состояниями НКА

Операция	Описание
-closure(s)	Множество состояний НКА, достижимых из состояния s только по  переходам
-closure(T)	Множество состояний НКА, достижимых из какого-либо состояния s из Т только по -переходам
move(T, a)	Множество состояний НКА, в которые имеется переход из какого-либо состояния s из Т по входному символу а

Перед тем как рассматривать первый входной символ, N может быть в любом из состояний множества -closure(s₀), где s₀ – стартовое состояние N. Предположим, что состояния множества T, и только они, достижимы из s₀ после прочтения данной последовательности входных символов, и пусть а – следующий входной символ. Получив а, N может переместиться в любое состояние из множества move(T, а). Совершив из этих состояний все возможные -переходы, N после обработки а может быть в любом состоянии из -closure (move(T, a)).

Построение НКА по регулярному выражению

Имеется немало стратегий построения распознавателей на основе регулярных выражений. Каждая из них имеет свои достоинства и недостатки. Одна из стратегий, используемая во многих текстовых редакторах, состоит в построении НКА на основе регулярного выражения и последующем моделировании его поведения.

Рассмотрим алгоритм построения НКА на основе регулярного выражения. Имеется множество вариаций этого алгоритма, и здесь будет представлен вариант, легкий в реализации. Алгоритм синтаксически управляем, поскольку использует в процессе построения синтаксиче-скую структуру регулярного выражения. Ветвления алгоритма соответствуют ветвлениям опреде-ления регулярного выражения. Вначале покажем, как строится автомат для распознавания  и лю-бого символа из алфавита. Затем определим, как конструируется автомат для выражений, содержа-щих операторы объединения, конкатенации или замыкания Клини. Например, для выражения r  s индуктивно построим НКА из автоматов для r u s.

В процессе создания НКА каждый шаг вносит не более двух новых состояний. В результате НКА, построенный по регулярному выражению, имеет количество состояний, превышающее число символов и операторов в регулярном выражении не более чем в два раза.