2. Условная максимизация

Этот способ также использует тот факт, что различные критерии обычно не равнозначны между собой. Здесь выделяется основной, главный критерий, а остальные рассматриваются как дополнительные, или сопутствующие.

Задача выбора, таким образом, формулируется как задача нахождения условного экстремума основного критерия:

x^* = arg {max q₁(x)|_qi(x)=Ci}, (7)

xX

при условии, что дополнительные критерии остаются на заданных им уровнях. Так, рис. 1б иллюстрирует решение задачи

x^* = arg {max q₂(x)|_q1(x)=C1},

xX

В некоторых задачах оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не столь жестко как в (7). Например, если сопутствующий критерий характеризует стоимость затрат, то вместо фиксации затрат разумно задавать их верхний уровень, т.е. формулировать задачу с ограничениями типа неравенств:

На рис. 2 приведено решение задачи

x₂^* = arg {max q₂(x)|_{q1(x) C1}}.

xX

Нетрудно увидеть, что здесь мы переходим к задаче математического программирования (линейного или нелинейного, в зависимости от видаq₂(x)).

Этот метод, таким образом, использует концепцию разной значимости критериев и ограничений на критерии. В приведенных выше примерах различие между основным и дополнительными критериями выглядит слишком сильным. Возможен другой вариант этого метода - метод уступок.

Пусть частные критерии упорядочены в порядке убывания их важности. Возьмем первый из них и найдем наилучшую по этому критерию альтернативу. Из рис. 2 видно, что если самым важным является критерий q₂ наилучшая альтернатива - это х₂*, если же самым важным является критерий q₁, то наилучшая альтернатива - х₄. Затем определяется «уступка» q_i, т.е. величина, на которую мы готовы уменьшить достигнутое значение самого важного критерия, чтобы за счет уступки попытаться увеличить значение следующего по важности критерия. На рисунке - альтернативы, полученные таким образом, изображены точками х₃* и х₅*.

3. Поиск альтернативы с заданными свойствами

Этот способ относится к случаю, когда значения частных критериев или их границы могут быть заданы, и задача состоит в том, чтобы (одно из двух):

1) найти альтернативу, удовлетворяющую эти требованиям;

2) если установлено, что такая альтернатива на множестве Х отсутствует, найти в Х альтернативу, которая подходит к поставленным целям более всего.

Характеристики решения такой задачи (сложность процесса вычислений, скорость сходимости, конечная точность) зависят от многих факторов.

Удобство метода. Здесь возможно задавать желательные значения критерия как точно, так и в виде верхних или нижних границ. Назначаемые таким образом значенияназывают иногда«уровнями притязаний», а точка их пересечения в р-мерном пространстве критериев - целью, опорной точкой, идеальной точкой. При этом важно отметить следующее:

поскольку уровни притязаний задаются без точного знания структуры множества Х в пространстве частных критериев, целевая точка может оказаться как внутри, так и вне Х. Это соответствует достижимой или недостижимой цели. На рис.3 приведены оба варианта - соответственно точки х₁* и х₂*.

И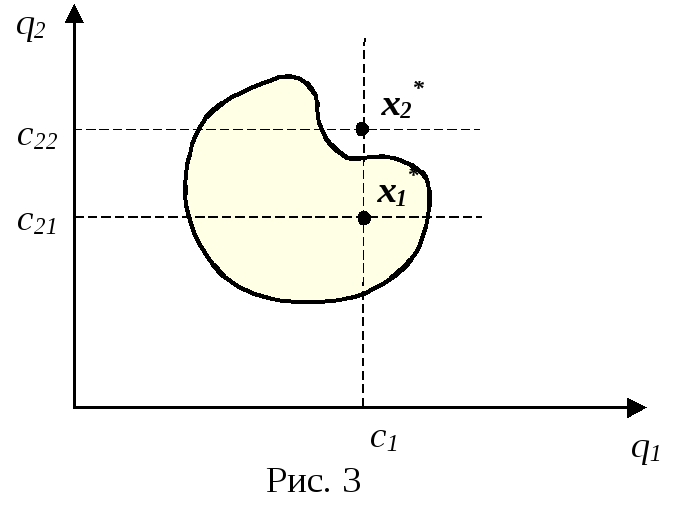дея оптимизации состоит в том, чтобы, начав с определенной альтернативы, приближаться кх* по некоторой траектории в пространстве Х. Для этого вводится числовая мера близости между очередной альтернативой х и целью х*, т.е. между векторами q(x)=(q₁(x),q₂(x),….q_p(x)) и Количественно эта близость может быть описана по-разному, например, расстояния типа:

S(q,) = min_i(q_i - )+_p+1, (9)

i

где считается, что q_i  , _i - коэффициенты, приводящие слагаемые к одинаковой размерности и одновременно учитывающие равную важность критериев. _p+1 учитывает наше отношение к тому, что важнее - увеличить близость к цели любого из частных критериев или же суммарную близость всех критериев к целевым значениям.