3. Геометрическая интерпретация задачи нелинейного

программирования

При числе переменных не более двух задачу НП можно решить геометрическим способом.

Процесс нахождения решения задачи НП (1), (2) с использованием ее геометрической интерпретации включает следующие этапы:

1. Находят ОДР задачи, определяемую соотношением (2); если она пуста, то задача не имеет решения.

2. Строят гиперповерхность f (x₁, x₂, … x_n) = h.

3. Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции (1) сверху (снизу) на множестве допустимых решений.

4. Находят точку ОДР, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют значение функции (1).

Пример.

Найти max функции f = x₂  x₁² + 6x₁ (3)

При условиях

2х₁ + 3х₂  24

х₁ + 2х₂  15

3х₁ + 2х₂  24

х₂  4,

х₁ ,х₂  0.

Решение: F нелинейна, следовательно, это задача НП;

1. ОАВС - ОДР

Следовательно, нужно определить такую точку многоугольника ОАВС, в которой функция принимает max значение.

2. Построим линию уровня F = x₂  x₁² +6x₁ = h,

где h – некоторая постоянная, и исследуем ее поведение при различных h. При каждом h получаем параболу, которая тем выше относительно ОХ, чем больше h.

Действительно,

F = x₂  x₁² +6x₁ = h =  парабола x₂ = x₁² - 6x₁ – h или х₂ = (х₁ – 3)²+h-9.

Р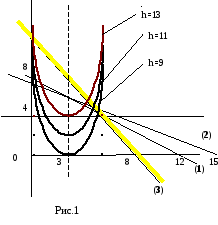 ассмотрим h = 9 х₂ = (х₁ – 3)²

h = 11 х₂ = (х₁ – 3)² + 2

h = 13 х₂ = (х₁ – 3)² + 4

Функция F принимает максимальное значение в точке касания одной из парабол с границей многоугольника ОАВС. В данном случае это точка Д, в которой линия уровня F = x₂  x₁² +6x₁ = 13 касается стороны многоугольника ОАВС.

П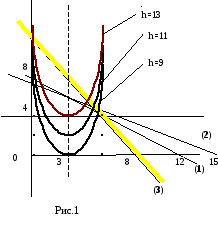 ри каждом h получаем параболу, которая тем выше отн. ОХ, чем больше h.

Действительно,

F = x₂  x₁² +6x₁ = h =  парабола x₂ = x₁² - 6x₁ – h или х₂ = (х₁ – 3)²+h-9

Рассмотрим h = 9 х₂ = (х₁ – 3)²

h = 11 х₂ = (х₁ – 3)² + 2

h = 13 х₂ = (х₁ – 3)² + 4

Координаты точки D находим из уравнений, соответствующих преобразованным ограничениям (1) и (2):

x₂  x₁² +6x₁ = 13, х₂ = 4, откуда х₁* = 3; х₂* = 4.

U_max, F_max = 13 при х* = (3;4).

Таким образом в этой задаче точка F_max не является вершиной треугольника решений. Поэтому процедура перебора вершин, которая использована в задачах ЛП неприменима.

4. Метод множителей Лагранжа

Математическая постановка. Рассмотрим частный случай общей задачи НП (1), (2), предполагая, что система ограничений (2) содержит только уравнение, отсутствуют условия неотрицательности переменных, и f (X₁, X₂ …X_n) и q_i (X₁, X₂,…X_n) – функции, непрерывные вместе со своими частными производными.

f (X₁, X₂ …X_n)  max (min)

q_i (X₁, X₂,…X_n) = b_i (I = 1, m).

Это так называемая задача на условный экстремум или классическая задача оптимизации.

Чтобы найти решение этой задачи, вводят набор переменных ₁, ₂,…_n, называемых множителями Лагранжа, составляют функцию Лагранжа.

f (X₁, X₂ …X_n, ₁, ₂,…_n) = f (X₁, X₂ …X_n) +

находят частные производные.

и рассматривают систему n + m уравнений.

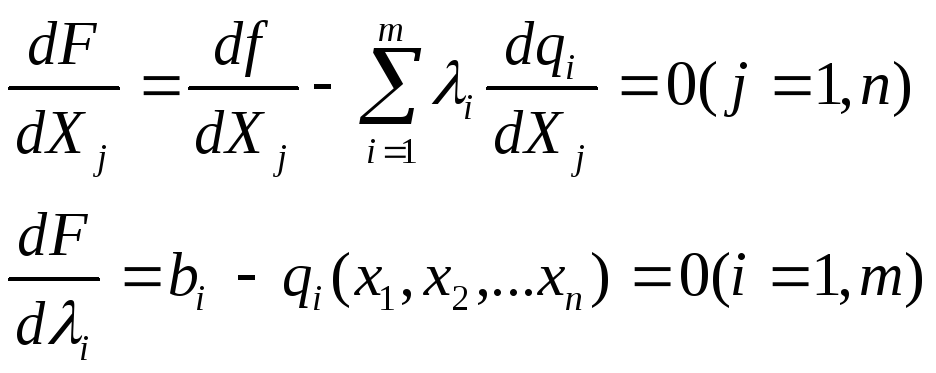
с n+m неизвестными Х₁, Х₂,…Х_n, _n, ₁, ₂,… _m.

Всякое решение этой системы уравнений определяет точку Х* = (Х₁*, Х₂, … Х_n), в которой может иметь место экстремум функции f (x₁, x₂,…x_n).

Следовательно, решив систему уравнений, получают все точки, в которых функция f (x₁, x₂,…x_n) может иметь экстремальные значения.

Таким образом, определение экстремальных точек задачи НП методом множителей Лагранжа включают следующие этапы:

1. Составляют функцию Лагранжа.

2. Находят частные производные от функции Лагранжа по переменным Х₁ и ₁ и приравнивают их нулю.

3. Решая полученную систему уравнений, находят точки, в которых целевая функция задачи может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, а вычисляют значения целевой функции в этих точках.

Пример:

По плану производства предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве Х₁ изделий I способом приведенная масса токсичных отказов равна 4Х₁ + Х₁² кг, а при изготовлении Х₂ изделий II способом они составляют 8х₂ + х₂² кг.

Определить, сколько изделий каждым из способов следует изготовить, чтобы общая масса отходов была минимальной.

Решение:

Математическая постановка задачи состоит в определении минимального значения функции

f = 4x₁ + x₁² + 8x₂ + x₂²

при условиях х₁ + х₂ = 180, х₁, х₂  0.

Теперь решим задачу, используя метод множителей Лагранжа. Найдем min целевой функции при условии х₁+х₂ = 180, но без учета требований неотрицательных переменных.

1. Составим функцию Лагранжа:

F(x₁, x₂,) = 4x₁+x₁²+8x₂+x₂²+(180-x₁ – x₂)

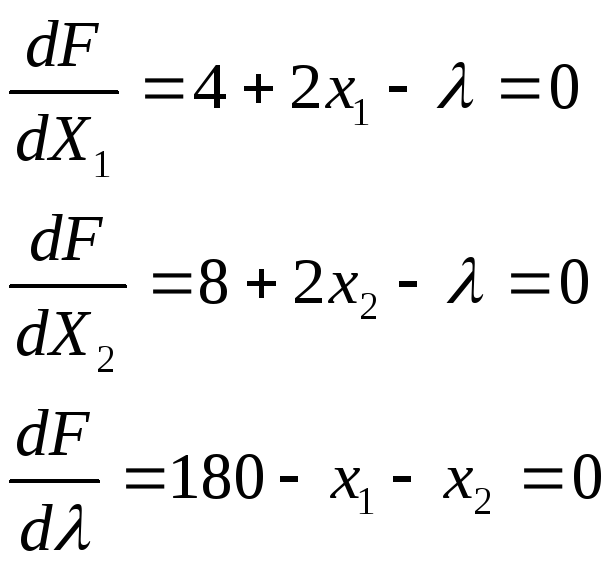
2. Вычисляем частные производные и приравниваем к нулю:

Перенося в правые части первых двух уравнений  и приравнивая их левые части:

4 + 2х₁ = 8+2х₂ или х₁ – х₂ = 2

Решая это уравнение совместно с последним:

х₁ – х₂ = 2

180-х₁-х₂ = 0, находим: х₂ = х₁-2

180-х₁ – х₁+2 = 0 х₁ = 91; х₂ = 89.

Этот результат и был получен выше, однако ММЛ более универсален, т.к. применим при n  2.

5. Обзор рассмотренных методов. Математическое

программирование и исследование операций

Рассмотренные нами методы линейного и нелинейного программирования (а также целочисленное программирование, динамическое программирование) объединяются понятием математическое программирование. Математическое программирование как и другие методы решения экстремальных задач составляют основу аппарата исследования операций - дисциплины, которая является одним из истоков системного анализа. Фактически, основные концепции, принципы анализа систем являются развитием теории исследования операций, и ее методы являются сегодня одной из основных глав системного анализа.

Сам термин «исследование операций» возник в послевоенные годы, когда стало ясно, что задачи широкого класса, возникшие в самых различных сферах человеческой деятельности, имеют, несмотря на их качественное различие, одно общее - они сводятся к выбору способа действия, варианта плана, параметров конструкции и т.п., т.е. к принятию решений, и этого общего достаточно для построения единой теории и единой системы методов. Создание сложных технических систем, проектирование сложных народнохозяйственных комплексов, анализ экологических ситуаций и многие другие направления инженерной, научной и хозяйственной деятельности требовали развития междисциплинарных, системных исследований. В этих условиях возник и весьма общий термин - «операция», означающий любое целенаправленное действие. Говоря об операции, мы всегда связываем с ней некоторого субъекта (оперирующую сторону), который формулирует цель операции и в интересах которого последняя проводится. Цель операции - обычно некоторый внешний (экзогенный) элемент - считается заданной.

Наряду с субъектом, т.е. с оперирующей стороной, мы всегда имеем дело еще и с исследователем операции. Он действует в интересах оперирующей стороны, и его задача состоит в том, чтобы найти способ использования ресурса (т.е. возможностей оперирующей стороны), обеспечивающий достижение цели.

Выше было сказано, что математическое программирование как и другие методы решения экстремальных задач составляют основу аппарата исследования операций, однако сама теория исследования операций не может быть сведена к решению экстремальных задач. Более того, исследование операций не является чисто математической дисциплиной и главные сложности анализа конкретных операций, как правило, заключаются не в математических трудностях.

Первым шагом исследования операций является формализация операции, ее описание с помощью языка математики. От того, как будет формализована задача, будет зависеть судьба исследования. Так простое описание делает и анализ более простым, но если модель не будет в достаточной степени адекватна реальности, то мы получим сомнительную достоверность результатов. Наоборот, переусложненная задача, учитывающая разнообразные детали процесса и с большими подробностями описывающая реальность, может привести к такой затрате машинного времени (большие системы), которую даже высокая точность результата не сможет оправдать.

Еще более сложные проблемы возникают при формировании критерия - способа оценки качества наших действий, когда необходимо сравнивать различные варианты стратегий, различные альтернативы. Здесь типична ситуация, когда операция оценивается несколькими показателями. В этом случае говорят о неопределенности целей. (Н.Н. Моисеев Математические задачи системного анализа. М.: Наука, 1981.)