Министерство образования Российской Федерации УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по использованию программы «AMACONT»

при структурной оптимизации технологических процессов в курсовом и дипломном проектировании студентов, обучающихся по направлениям:

651400 – «Машиностроительные технологии и оборудование», 657800 – «Конструкторско-технологическое обеспечение

машиностроительных производств», 552900 – «Технология, оборудование и автоматизация

машиностроительных производств»

Уфа 2002

Составитель М.А. Анфёров

УДК 621.9:519.673

Методические указания по использованию программы «AMACONT» при структурной оптимизации технологических процессов в курсовом и дипломном проектировании студентов, обучающихся по направлениям: 651400 – «Машиностроительные технологии и оборудование», 657800 – «Конструкторско-технологическое обеспечение машиностроительных производств», 552900 – «Технология, оборудование и автоматизация машиностроительных производств» / Уфимск. гос. авиац. техн. унив-т; Сост. М.А. Анфёров.– Уфа, 2002.– 28 с.

Излагаются методические основы выполнения структурной оптимизации технологических процессов на уровне маршрутного описания, а также методика работы на ЭВМ с программой «AMACONT» при реализации вышеназванной оптимизации. Предназначены для обеспечения учебного процесса студентов, обучающихся по дневной и очнозаочной формам обучения по направлениям: 651400 – «Машиностроительные технологии и оборудование», 657800 – «Конструкторскотехнологическое обеспечение машиностроительных производств», 552900 – «Технология, оборудование и автоматизация машиностроительных производств», на этапах выполнения курсовой работы по дисциплине «Системный анализ и математическое моделирование процессов в машиностроении» и дипломного проектирования по тематике, связанной с техническим перевооружением и конверсией действующих машиностроительных производств.

Табл.2. Ил.19. Библиогр.: 8 назв.

Рецензенты:

3

Содержание

Стр.

1Многокритериальная структурная оптимизация технологических процессов на уровне маршрутного

4

Введение

Динамика современного машиностроительного производства в развитых странах, вынужденное техническое перевооружение отечественных предприятий, вызванное регрессионными процессами в период перехода экономики страны к рыночным отношениям, конверсия предприятий оборонно-технического комплекса – все это требует реализации процесса научно-технического развития производства, технологическая подготовка которого предполагает в качестве центрального ее этапа разработку перспективных (проектных) технологических процессов (ПТП). Проектирование ПТП осуществляется на основе системной многоуровневой оптимизации, определяющую роль в которой занимает структурная оптимизация, носящая многоуровневый и многокритериальный характер, выполняемая в условиях повышенной неопределенности и недостаточности информационного пространства /1–

2/.

В связи с этим дипломные проекты студентов, обучающихся по направлениям: 651400 – «Машиностроительные технологии и оборудование», 657800 – «Конструкторско-технологическое обеспечение машиностроительных производств», 552900 – «Технология, оборудование и автоматизация машиностроительных производств», тематика которых отвечает решению выше обозначенных проблем, являются особо актуальными. Неотъемлемой частью этих проектов является разработка ПТП с интенсивным использованием CAD/CAM-систем

(Unigraphics, Pro/Engineer, Cimatron, Euklid и др. ), экспертных оболо-

чек, САПР ТП на основе структурной оптимизации на уровне маршрутного описания.

Приобретение студентами практических навыков структурной многокритериальной оптимизации ПТП с использованием метода «AMACONT» /3/ осуществляется при выполнении ими курсовой работы в рамках учебной дисциплины «Системный анализ и математическое моделирование процессов в машиностроении».

Данные методические указания являются методическим обеспечением работы студентов на ПЭВМ со специальной программой «AMACONT» при реализации вышеназванной оптимизации при курсовом и дипломном проектировании. Особо полезными они являются для студентов очно-заочной формы обучения, самостоятельно осваивающих работу с этой программой.

5

1 Многокритериальная структурная оптимизация технологических процессов на уровне маршрутного описания

Системный подход к решению сложных технических задач, основывается на анализе и синтезе структуры, функции и характеристик рассматриваемого объекта. Все системное рассмотрение осуществляется через призму структуры объекта, под которой понимается совокупность устойчивых отношений между частями целостного объекта. Подробно ознакомиться с определениями и содержанием структурных элементов технологического процесса можно в соответствующей литературе /2, 4/.

При использовании системного подхода при оптимизации технологических процессов предусматривается, во-первых, определение цели оптимизации путем рассмотрения самой технологии как сложной системы, а, во-вторых, выявление ее системных связей с системами более высокого уровня - проектирующей и производственной.

Задачу оптимизации можно определить как поиск наилучшего решения sopt из множества допустимых SD= {sj}, j [1,n] по заданному

Следует заметить, что множество SD является допустимым с точки зрения функции оптимизируемой системы. Например, по отношению к технологическому процессу это говорит о том, что какую бы структуру технологии из множества SD мы не выбрали, в любом случае получится годная деталь в соответствии со всеми требованиями ее рабочего чертежа.

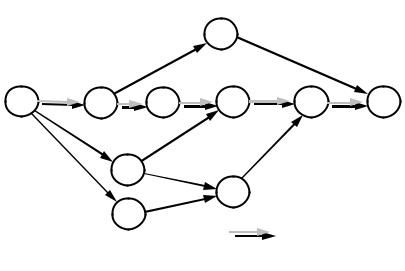
Для формирования вышеназванного допустимого множества решений используются математические модели. При выполнении структурной оптимизации технологических процессов на уровне их маршрутного описания используется сетевой граф G=(X,U). Вершинами X такого графа являются элементы множества образов возможных вариантов технологических операций, отличающихся концентрацией, используемыми технологическими методами (в том числе при получении исходной заготовки) и оборудованием. Дуги графа U – это образы логических связей возможности последовательного выполнения пар соответствующих технологических операций.

6

Формирование модели осуществляется путем анализа возможных многовариантных технологических структурных решений, а именно:

–различной концентрации операций;

–различного технологического оборудования выполнения опе-

рации;

–различного уровня автоматизации;

–различных технологических методов.

На рисунке 1.1 показан пример модели, построенной путем анализа возможных многовариантных технологических структурных решений, а именно:

–различной концентрации технологических операций (операция,

соответствующая вершине x7 , включает в себя переходы операций, соответствующих вершинам x2 и x3 );

–использования технологического оборудования с различной

степенью автоматизации (операции, соответствующие вершинам x7 и x8 , выполняются на альтернативных станках1, например 16У04П 16Б05АФ1);

–различных технологических методов (операции, соответст-

вующие вершинам x4 и x9 , выполняются альтернативными технологическими методами, например, сверлением и электроэрозионной обработкой).

Любой полный путь Lj = { xi } , xi X на таком графе, соединяющий вершины входа и выхода сети (для рассматриваемого примера

– это вершины x1 и x6 ), является отображением допустимого варианта структуры технологического процесса.

В отличие от иллюстрирующего примера математическая модель реального технологического процесса представляет из себя граф с об-

щим количеством путей , достигающим порядка 1030.

Поставив в соответствие каждой вершине графа xi X вещественное число ε o(xi), представляющее из себя значение функционального выходного параметра, соответствующего тому или иному критерию

1 Предполагается, что характеристики рассматриваемых станков (мощность, габариты, технологические возможности и др.) соответствуют условиям обработки данной заготовки.

Решение многокритериальных оптимизационных задач осуществляется двумя подходами /2/ - с использованием обобщенного критерия оптимизации, в который сворачиваются все критерии, и так называемой "пороговой оптимизацией".

Основу метода пороговой оптимизации структуры технологического процесса на уровне маршрутного описания составляет построение по основному критерию упорядоченного множества путей графа, отвечающих следующим требованиям: если t - это порядковый номер пути, то

o

где {Lj } – множество длин всех путей графа, рассчитанных по основ-

ному критерию1.

Для реализации поиска путей графа, составляющих вышеназванное упорядоченное множество2 SD = {Lj} следует воспользоваться алгоритмом из класса так называемых алгоритмов "поиска k-кратчайших путей". В качестве такого можно рекомендовать алгоритм AMACONT /6/, который для данного класса графов на порядок превосходит по времени сходимости известные алгоритмы (например, алгоритм

"double sweep" /7/ ).

Второстепенные критерии оптимизации формируют ограничения следующего вида

где Lk - пороговое значение на длину пути по k-му второстепенному критерию (см. (1.3)). Причем, ограничение сверху вводится если критерий оптимизации предполагает минимизацию соответствующего параметра и длины пути, так как противоречивость критериев приведет к его увеличению, на которое и необходимо ввести ограничение. Что касается ограничения снизу, то здесь мы имеем обратные рассуждения.

Ниже приводится алгоритм реализации пороговой структурной оптимизации.

Шаг 1. Назначить основной ε o(xi) и второстепенные { ε k(xi) } (xi X) критерии оптимизации. Второстепенные критерии не помечены.

Шаг 2. Назначить (экспертно) для каждого k-го второстепенного кри-

терия пороговое значение Lk на длину пути графа. Шаг 3. Положить t = 1.

1 Номер основного критерия условно принят за 0.

2 Обратите внимание, что речь идет о допустимом множестве.

10

o

Шаг 4. Найти t-й элемент упорядоченного множества1 SD , т.е. Lt .

Шаг 5. Выбрать любой непомеченный второстепенный критерий. Если такой критерий найден – пометить его и перейти к шагу 6. Если поиск

o

неудачен, закончить процедуру – оптимальным является путь Lt .

o

Шаг 6. Проверить для пути Lt выполнение неравенства (1.5) по вы-

бранному на шаге 5 критерию. Если неравенство справедливо – перейти к шагу 5. В противном случае – снять метки со всех второстепенных критериев, увеличить t на единицу (t = t + 1) и перейти к шагу 4.

Используемая для пороговой оптимизации компьютерная программа «AMACONT» /8/ позволяет получить упорядоченное множество (1.3), которое далее уже экспертно анализируется на предмет ограничений (1.5) с выбором оптимального решения. Это бывает необходимо при учете неформализуемых, например социальных, второстепенных критериев, которые не определяются каким либо параметром и для которых не возможно, следовательно, ввести ограничения (1.5). В этом случае данные критерии учитываются на шаге 6 в виде дополни-

o

тельного анализа пути Lt . Такой способ полезен также при необходи-

мости попутной корректировки пороговых значений, что повышает гибкость и наглядность принимаемых решений, дает возможность дополнительного анализа при оптимизации.

При необходимости в рамках системы «AMACONT» можно сразу ввести пороговые значения для второстепенных критериев, с учетом которых и будет получаться оптимальное решение, удовлетворяющее ограничениям (1.5). Однако при этом необходимо иметь ввиду, что в случае чрезмерного ужесточения пороговых ограничений, решения можно не получить совсем.

Что касается использования при структурной оптимизации обобщенного критерия ε Σ , то это не вызывает никаких затруднений, хотя и делает процесс оптимизации менее эффективным (см. /4/). Суть данной процедуры сводится к следующему.

1 См. (1.4).