Уфимский Государственный Авиационный Технический Университет

Кафедра АСУ

Расчетная работа

по дисциплине

«Системный анализ и исследование операций»

Вариант 18

Выполнила: ст. гр. АСОИ-325 Шакирова Л.Р.

Принял: Бабак С.Ф.

Уфа 2005

Задача коммивояжера

Задание:

Решить задачу коммивояжера по следующим данным:

	1	2	3	4	5	6
1	-	50	33	18	5	44
2	51	-	19	24	20	32
3	19	23	-	42	14	25
4	42	53	2	-	48	5
5	27	28	31	33	-	1
6	12	37	60	21	21	-

Решение:

Приведем данную матрицу по строкам и по столбцам, получим:

Сложив приведение по строкам и по столбцам, получим: 53 + 14 = 67.

Следовательно, Min оценка = 67.

Оценим нули в полученной матрице:

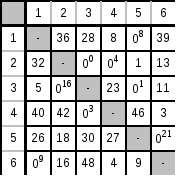
Max оценка = 21.

Разбиваем на 5,6 и not 5,6.

Минор по 5,6.

Вводим запрет на 6,5.

Оценим нули в полученной матрице:

Max оценка = 40.

Разбиваем на 4,3 и not 4,3.

Минор по 4,3.

Вводим запрет на 3,4.

Оценим нули в полученной матрице:

Max оценка = 16.

Разбиваем на 3,2 и not 3,2.

Минор по 3,2.

Вводим запрет на 2,4.

Приводим матрицу по 2 строке и 4 столбцу.

Оценим нули в полученной матрице:

Max оценка = 31.

Разбиваем на 6,1 и not 6,1.

Минор по 6,1.

Вводим запрет на 1,5.

Приводим матрицу по 4 столбцу.

В итоге получим дереве ветвлений и длин путей:

По этому дереву можно определить, что оптимальным путем является последовательность:

5  6  4  3  2  1  5 и его длина равна 76.

Вывод:

Путь является оптимальным, по данному методу, но является и наикротчайшим (в соответствии с методом прямого перебора).

Дискретная задача транспортного типа

Задание:

Решить транспортную задачу по следующим данным:

Задача максимизации.

Решение:

Приведем задачу максимизации к задаче минимизации:

Приведем данную матрицу по строкам и по столбцам, получим:

Сложив приведение по строкам и по столбцам, получим: -75 + 6 = -69.

Следовательно, Min оценка = -69.

1. Оценим нули в полученной матрице:

Max оценка = 9.

Разбиваем на 7,4 и not 7,4.

Минор по 7,4.

2. Оценим нули в полученной матрице:

Max оценка = 2.

Разбиваем на 2,3 и not 2,3.

Минор по 2,3.

3. Оценим нули в полученной матрице:

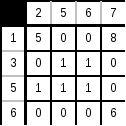
Max оценка = 5.

Разбиваем на 4,1 и not 4,1.

Минор по 4,1.

4. Оценим нули в полученной матрице:

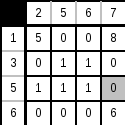
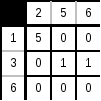
Max оценка = 1.

Разбиваем на 5,7 и not 5,7.

Минор по 5,7.

5. Оценим нули в полученной матрице:

Max оценка = 1.

Разбиваем на 3,2 и not 3,2.

Минор по 3,2.

6. Завершаем цикл:

Вводим недостающие ребра: 6,6 и 1,5.

В итоге получим дерево ветвлений и длин путей:

По этому дереву можно определить, что оптимальным путем является последовательность:

7 è 4 è 1 è 5 è 2 è 3 è 6 è 5 и его длина равна (при переходе к задаче максимизации домножаем на -1).

Вывод:

Путь является оптимальным, по методу «ветвей и границ», в данной модели нет строгого правила: обход каждой вершины по одному разу, поэтому допускается как переход из вершины в туже вершину, так и проход через одну вершину несколько раз. Однако для данной постановки задачи наиболее удачным является гамильтонов цикл.

7