Лабораторная работа №5

Множественная регрессионная модель.

Классическая линейная модель

Классическая (нормальная) модель линейной множественной регрессии (КЛММР) имеет вид:

(1)

где - значение результирующей переменной; - значение 1-го, 2-го,…, р-го регрессора в i-ом наблюдении (i = 1,2,…,n); β_0, β_1, β_p - числовые коэффициенты; ε_i - случайные (стохастические) составляющие или ошибки (возмущения).

Переписывая выражение (1) в виде системы уравнений для различных значений (i = 1,2,…,n), их можно представить в матричном виде:

_, (2)

где - вектор объясняемых переменных;

ε= - вектор значений ошибки; - вектор коэффициентов;

X= - матрица объясняющих переменных размером n×(p+1), в которой первый столбец с единичными элементами соответствует в выражении (1) умножению на единицу.

Основные предпосылки (гипотезы) КЛММР:

1. Х – детерминированная матрица.

2. Математическое ожидание возмущения ε₀ равно нулю:

( i = 1,2,…,n),

где М[·] знак математического ожидания.

3. Дисперсия возмущения постоянна для любых значений i (условие гомоскедастичности):

( i = 1,2,…,n),

где D[·] знак дисперсии;

- величина дисперсии.

4. Возмущения для разных наблюдений являются некоррелирован­ными:

при ,

где - коэффициент ковариации.

Условия 3 и 4 можно объединить в одно, определяющее вид ковариа­ционной матрицы возмущений:

C_ε = =

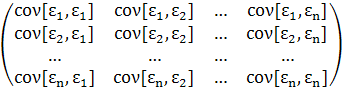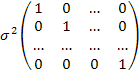= = = =M[ε ]= ,

где - векторное произведение векторов;

Т – знак транспонирования матрицы;

_In - единичная матрица n-го порядка.

5. Возмущения являются нормально распределёнными случайными вели­чинами с нулевым средним значением и дисперсией :

или .

6. Векторы объясняющих переменных (столбцы матрицы Х) линейно не­зависимы (ни один из них не может быть представлен в виде линейной комбинации других), другими словами, ранг матрицы Х равен числу её столбцов:

.

Для получения уравнения регрессии достаточно первых четырёх и шестой предпосылок. Требование выполнения пятой предпосылки необхо­димо для оценки точности уравнения регрессии и его параметров.

Традиционный метод наименьших квадратов (мнк)

Оценкой модели (1) по выборке при (i = 1,2,…,n) является уравнение:

(3)

которое можно представить в матричном виде:

(4)

г де = - вектор аппроксимирующих значений зависимой переменной;

b= вектор выборочных оценок коэффициентов соответственно.

Согласно МНК, вектор неизвестных переменных параметров b выбира­ется так, чтобы сумма квадратов остатков была минимальной:

, (5)

или с учётом (4) в матричной записи ( - скалярное произведение векто­ров):

. (6)

Необходимые условия экстремума (6) находятся путём приравнивания вектора частных производных: .

Отсюда в результате приведения выражения (6) к более удобному для дифференцирования виду , с учётом известных из линейной алгебры правил вычисления производных по векторному аргу­менту (с и А – вектор и симметричная матрица соот­ветственно) получается система нормальных уравнений для определения вектора b:

(7)

Согласно предпосылке 6 КЛММР, ранг матрицы Х равен р+1. Это оз­начает, что ранг симметричной квадратной матрицы р+1-го порядка также равен р+1, она является невырожденной (её определитель не равен нулю), и существует обратная матрица такая, что произведение . Поэтому решение системы (7) можно представить сле­дующим образом:

. (8)

Если записать первое уравнение системы нормальных уравнений (7) в развернутом виде:

легко получить соотношение, выражающее коэффициент через осталь­ные коэффициенты и соответствующие выборочные средние:

. (9)