
- •Содержание
- •Лабораторная работа №6. Задачи оптимизации 46
- •Введение
- •Лабораторная работа №1
- •1. Обработка результатов многократных измерений одной и той же величины
- •2. Обработка результатов нескольких серий измерений одной и той же величины
- •Лабораторная работа №2
- •Корреляционно-регрессионный анализ
- •Лабораторная работа №3
- •Лабораторная работа №4
- •Варианты для парной регрессионной модели
- •Лабораторная работа №5
- •Традиционный метод наименьших квадратов (мнк)
- •Статистические свойства вектора оценок коэффициентов регрессии
- •Теорема Гаусса-Маркова
- •Несмещённые оценки дисперсии ошибок, ковариационной матрицы и дисперсии выборочных коэффициентов регрессии
- •Оценка значимости и доверительных интервалов для коэффициентов регрессии
- •Анализ вариации зависимой переменной
- •Значения сумм квадратов
- •Значения дисперсий
- •Выборочный коэффициент детерминации
- •Скорректированный коэффициент детерминации
- •Оценка значимости уравнения регрессии
- •Доверительный интервал для значений зависимой переменной
- •Пример оформления лабораторной работы
- •Задания для модели множественной регрессии
- •Варианты для множественной регрессионной модели
- •Лабораторная работа №6 Задачи оптимизации
- •Задача линейного программирования о смесях
- •Лабораторная работа №7
- •Варианты на решение задачи о продуктивности модели Леонтьева
- •Лабораторная работа №8
- •Библиографический список
- •Приложение
- •3. Критические точки распределения χ2
- •Сахабиева Галина Александровна
- •Васяйчева Вера Ансаровна
- •Орлова Людмила Викторовна
- •443084, Г. Самара, ул. Стара-Загора, 96
- •4 43080, Г. Самара, ул. Революционная, 70п
Анализ вариации зависимой переменной
Общая
сумма квадратов отклонений
![]() разбивается на два слагаемых:
разбивается на два слагаемых:
![]() ,
(24)
,
(24)
где
![]() ,
,
![]() - соответственно факторная и остаточная
суммы квадратов.
- соответственно факторная и остаточная
суммы квадратов.
По аналогии со случаем парной регрессии эти суммы можно выразить через вектор выборочных коэффициентов b и выборочный коэффициент детерминации (табл. 8):
![]()
Значения сумм квадратов
Таблица 8
Название |
Общее выражение |
Выражение через b |
Выражение
через
|
Общая |
|
|
|
Факторная |
|
|
|
Остаточная |
|
|
|
При делении суммы квадратов на число её степеней свободы получается несмещённая оценка соответствующей дисперсии (табл. 9).
Значения дисперсий
Таблица 9
Название |
|
Выражение |
Общая |
|
|
Факторная |
|
|
Остаточная |
|
|
Выборочный коэффициент детерминации
Выборочный множественный коэффициент детерминации показывает качество подгонки регрессионной модели к наблюдаемым значениям и определяется выражением (в отличие от случая модели парной регрессии он обозначается ):
![]() (25)
(25)
Свойства коэффициента :
Коэффициент служит для оценки значимости (качества) уравнения регрессии, является одной из наиболее эффективных оценок адекватности регрессионной модели, характеристикой её прогностической силы.
Коэффициент при выполнении 5-го условия КЛММР является состоятельной, но смещённой оценкой генерального коэффициента детерминации , с математическим ожиданием и дисперсией, приближённо определяемыми выражениями:
![]() ;
;
![]() .
.
Коэффициент - безразмерная величина, лежащая в пределах 0

 1.
1.При =0 вариация зависимой переменной полностью обусловлена воздействием неучтённых в модели переменных и линия регрессии не улучшает качество предсказания значений по сравнению с тривиальным предсказанием

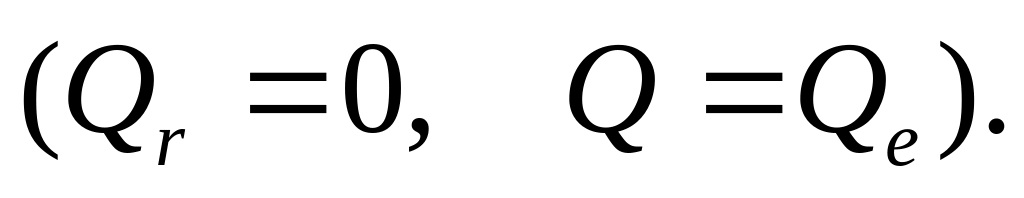
При =1 осуществляется точная подгонка и все эмпирические точки удовлетворяют уравнению регрессии

Коэффициент может быть вычислен из матрицы парных коэффициентов корреляции по формуле:
![]() , (26)
, (26)
где
![]() - определитель симметричной квадратной
матрицы выборочных парных коэффициентов
корреляции
- определитель симметричной квадратной
матрицы выборочных парных коэффициентов
корреляции
![]() -
го порядка
-
го порядка
![]() =
= (27)
(27)
с
элементами
![]()
![]() , (28)
, (28)
![]() , (29)
, (29)
где
![]() ;
;
![]() ;
;
![]() =
=![]() ,
где
,
где
![]() =
=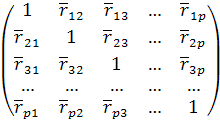 . (30)
. (30)
Выражение
(26) определяет выборочный множественный
коэффициент детерминации р-го
порядка (по числу р
объединяющих переменных). Множественные
коэффициенты детерминации низших
порядков определяются аналогичным
образом из соответствующих подматриц
матриц
![]() .
.
Так,
выборочный множественный коэффициент
детерминации 1-го
порядка
![]() ,
равный квадрату парного коэффициента
корреляции между результирующей
,
равный квадрату парного коэффициента
корреляции между результирующей
![]() и
и
![]() -ой
объясняющей переменной
-ой
объясняющей переменной
![]() ,
находится по формуле:
,
находится по формуле:
![]() , (31)
, (31)
где
![]() - определитель подматрицы
- определитель подматрицы
![]() ,
получаемый из матрицы
,
получаемый из матрицы
![]() путём вычёркивания всех строк и столбцов
кроме тех, которые соответствуют
переменным
и
(первые
-е
строка и столбец);
путём вычёркивания всех строк и столбцов
кроме тех, которые соответствуют
переменным
и
(первые
-е
строка и столбец);
![]() -
алгебраическое дополнение 1-го
элемента 1-й
строки этой подматрицы.
-
алгебраическое дополнение 1-го
элемента 1-й
строки этой подматрицы.
Выборочный
множественный коэффициент детерминации
2-го порядка
![]() для объясняемой
для объясняемой
![]() и факторных переменных
,
и факторных переменных
,
![]() определяется выражением:
определяется выражением:
![]() , (32)
, (32)
где
![]() - определитель подматрицы
- определитель подматрицы
![]() ,
которая находится из матрицы
,
которая находится из матрицы
![]() в результате вычёркивания всех строк
и столбцов кроме тех, которые отвечают
,
и
;
- алгебраическое дополнение 1-го
элемента 1-й
строки полученной подматрицы.
в результате вычёркивания всех строк
и столбцов кроме тех, которые отвечают
,
и
;
- алгебраическое дополнение 1-го
элемента 1-й
строки полученной подматрицы.
Выборочные множественные коэффициенты детерминации более высоких порядков находятся аналогичным образом.
Величина , вообще говоря, возрастает при добавлении новых регрессоров (поскольку растёт
 ),
хотя это не обязательно означает
улучшение качества регрессионной
модели.
),
хотя это не обязательно означает
улучшение качества регрессионной
модели.
Поскольку присоединение в уравнение регрессии каждой новой предикторной переменной не может уменьшить величины коэффициента детерминации (независимо от порядка присоединения), множественные коэффициенты детерминации различных порядков удовлетворяют цепочке неравенств:
![]() . (33)
. (33)
Попыткой устранения эффекта, связанного с ростом при добавлении новых объясняющих переменных, является коррекция на число регрессоров.
