§2. Прапазiцыйныя формулы

Для абазначэння выказванняў, якія не пабудаваныя з іншых выказванняў з дапамогаю аперацыяў (такія выказванні будзем называць элементарнымі) будзем ужываць вялiкiя лiтары лацiнскага алфавiту i лiтары з iндэксамi , якiя будзем называць прапазiцыйнымi лiтарамi. Розныя літары будуць абазначаць розныя выказванні і кожная літара ў пэўным разважанні абазначае адно канкрэтнае выказванне.

Выразы, пабудаваныя з лiтараў з дапамогаю сымболяў логiкавых аперацыяў, будзем называць прапазiцыйнымi формуламi.

Папярэдні сказ нельга назваць азначэннем, ён не вытрымлівае крытыкі з пункту гледжання матэматыкі; паводле яго, напрыклад, выразы і былі б формуламі. Дамо дакладнае азначэнне прапазіцыйнай формулы:

Азначэнне. (a) Усе прапазiцыйныя лiтары ёсць прапазiцыйныя формулы.

(b) Калi i – прапазiцыйныя формулы, тады

, , , , –

таксама прапазiцыйныя формулы.

(с) Толькi тыя выразы з’яўляюцца прапазiцыйнымi формуламi, для якiх гэта вынiкае з (a) i (b).

Напрыклад, выразы i – прапазiцыйныя формулы, а выраз не ёсць прапазiцыйная формула (чаму?).

Практыкаванне 1. Вызначце, цi з’яўляецца паслядоўнасць сымболяў прапазiцыйнай формулай:

(1) ;

(2) ;

(3) ;

(4) ;

(5) ;

(6) ;

(7) ;

(8) .

Для абазначэння адвольных прапазіцыйных формулаў будзем ужываць вялікія літары лацінскага алфавіту і літары з індэксамі, надрукаваныя тлустым прапісным шрыфтам. Розныя такія літары не абавязкова абазначаюць розныя формулы (у адрозненне ад літараў, надрукаваных звычайным шрыфтам (прапазіцыйных літараў), якія абазначаюць розныя элементарныя выказванні).

Заўвага. Увядзем дамоўленасць пра ўжыванне дужкаў у запiсах прапазiцыйных формулаў. Па-першае, не будзем пісаць вонкавую пару дужкаў. Па-другое, калi прапазiцыйная формула мае ўваходжаннi толькi аднаго логiкавага злучнiку, будзем прапускаць вонкавыя дужкi ў той з формулаў, якая стаiць злева. Па-трэцяе, дамовiмся лiчыць злучнiкi ўпарадкаванымi наступным чынам: , i часам будзем прапускаць тыя пары дужкаў, без якiх магчымае аднаўленне формулы паводле наступнага правiла. Кожнае ўваходжанне знаку належыць да найменшай формулы, якая iдзе за iм; пасля таго, як расстаўлены дужкi, якiя належаць да ўсiх уваходжанняў знаку , кожнае ўваходжанне знаку злучае найменшыя формулы, якiя яго акружаюць, i г.д.. Пры дастасаваннi гэтага правiла да аднаго злучнiку мы рухаемся злева направа.

Прыклад 1. Замест пiшацца ; замест пiшацца .

Прыклад 2. У формуле дужкi аднаўляюцца наступнымi крокамi:

,

,

,

,

,

.

Практыкаванне 2. Выключыць магчыма большую колькасць дужкаў у формулах:

(1) ;

(2) ;

(3) .

Практыкаванне 3. Аднавiць дужкi ў формулах:

(1) ;

(2) ;

(3) .

Кожнаму размеркаванню лoгiкавых значэнняў лiтараў, якiя ўваходзяць у некаторую прапазiцыйную формулу, адпавядае, згодна з азначэннямi логiкавых аперацыяў, пэўнае логiкавае значэнне гэтай формулы. Такiм чынам, кожная прапазiцыйная формула, у якую ўваходзяць літараў, вызначае функцыю ад зменных на мностве {0,1} з значэннямi ў {0,1}, якую графiчна можна запiсаць у выглядзе таблiцы праўдзiвасцi для гэтай формулы. Напрыклад, формула

мае наступную таблiцу праўдзiвасцi:

1	1	1	0	1	1
1	1	0	0	1	0
1	0	1	0	1	1
1	0	0	0	1	0
0	1	1	1	1	1
0	1	0	1	1	0
0	0	1	1	0	0
0	0	0	1	0	0

Вiдавочна, што калi ў формулу ўваходзяць розных лiтараў, тады ў таблiцы праўдзiвасцi будзе радкоў, бо магчымыя розных размеркаванняў логiкавых значэнняў для лiтараў.

Азначэнне. Функцыя аргументаў, зададзеная на мностве з значэннямi ў , называецца булевай функцыяй аргументаў.

Такiм чынам, кожная прапазiцыйная формула вызначае пэўную булеву функцыю.

Напiсанне таблiцы праўдзiвасцi можна спрасцiць наступным чынам. Выпiсваем прапазiцыйную формулу, i для кожнага размеркавання логiкавых значэнняў лiтараў, якiя ўваходзяць у формулу, пад усiмi ўваходжаннямi кожнай з гэтых лiтараў пiшам адпаведнае логiкавае значэнне. Затым паслядоўна пад кожным логiкавым злучнiкам выпiсваем логiкавыя значэннi той часткi формулы, для якой гэты злучнiк дастасоўваецца апошнiм.

Прыклад 3. Для формулы маем

1	1	1	0	1	0	0	1
1	0	0	0	1	1	1	0
0	1	1	0	0	0	0	1
0	1	0	0	0	0	1	0

Азначэнне. Прапазiцыйная формула называецца таўталогiяй (тоесна праўдзiвай формулай), калi адпаведная ёй булева функцыя набывае значэнне 1 пры ўсiх наборах логiкавых значэнняў лiтараў, якiя ў яе ўваходзяць.

Прапазiцыйная формула з’яўляецца таўталогiяй калi i толькi калi ў яе таблiцы праўдзiвасцi слупок пад формулай складаецца толькi з 1. Тое, што формула таўталогiя, будзем запiсваць наступным чынам: ╞ .

Прыклад 4. Формула – таўталогiя (“закон вылучанага трэцяга”). Гэта вынiкае з таблiцы праўдзiвасцi для нашай формулы:

1	0	1
0	1	1

Практыкаванне 4. Даказаць, што наступныя прапазiцыйныя формулы ёсць таўталогii:

(1) ;

(2) ;

(3) ;

(4) ;

(5) ;

(6) ;

(7a) ;

(7b) ;

(8a) ;

(8b) ;

(9) ;

(10) ;

(11) ;

(12) ;

(13a) ;

(13b) ;

(14) ;

(15) ;

(16) ;

(17) ;

(18) ;

(19) ;

(20) ;

(21) (рэфлексіўнасць эквівалентнасці);

(22) (сіметрычнасць эквівалентнасці);

(23) (транзітыўнасць эквівалентнасці).

Азначэнне. Прапазiцыйная формула называецца супярэчнасцю (тоесна непраўдзiвай формулай), калi адпаведная ёй булева функцыя набывае значэнне 0 пры ўсiх наборах логiкавых значэнняў, што ўваходзяць у формулу.

Таблiца праўдзiвасцi для такой формулы мае ў слупку пад формулай толькi нулi. Вiдавочна, формула ёсць таўталогiя калi i толькi калi ёсць супярэчнасць.

Прыклад 5. Формула – супярэчнасць, бо таблiца праўдзiвасцi для яе мае выгляд:

1	0	0
0	1	0

Формула з прыкладу 3 – таксама супярэчнасць.

Азначэнне. Прапазiцыйныя формулы i называюцца логiкава эквiвалентнымi (раўназначнымi), калi ёсць таўталогiя.

У таблiцах праўдзiвасцi для логiкава эквiвалентных формулаў слупкi пад гэтымi формуламi аднолькавыя. Логiкава эквiвалентным формулам адпавядае тая сама булева функцыя. Логiкавая эквiвалентнасць формулаў i запiсваецца наступным чынам: .

Прыклад 6. . Для таго, каб даказаць логiкавую эквiвалентнасць гэтых формулаў, напiшам iхнiя таблiцы праўдзiвасцi:

1	1	1	0	1	1	0	1
1	0	0	1	0	0	0	1
0	1	1	0	1	1	1	0
0	1	0	1	0	1	1	0

Даведзеная логiкавая эквiвалентнасць абгрунтоўвае метад доказу ад супрацьлеглага.

Практыкаванне 5. Даказаць логiкавыя эквiвалентнасцi:

(1) (закон падвойнага адмаўлення);

;

;

;

;

(10) ;

(11) ;

;

;

(16) ;

(17) ;

(18) ;

(19) ;

(20) ;

(21) ;

(22) .

Непустое мноства элементаў, на якiм вызначаныя бiнарныя аперацыi складання, множання i ўнарная аперацыя адмаўлення, што задавальняюць (2) – (11) з практыкавання 5, называецца алгебрай Буля. Такiм чынам, мноства выказванняў з аперацыямi ёсць алгебра Буля. Яшчэ адзiн прыклад алгебры Буля – мноства ўсiх падмностваў некаторага мноства M у дачыненнi да бінарных аперацыяў аб’яднання, перасячэння i ўнарнай аперацыі ўзяць дадатак падмноства A да M.

Прыклад 7. Адмаўленне выказвання “Паліном непрыводны над і мае ступень 2” паводле закону дэ Моргана (гл. практыкаванне 5) раўназначнае выказванню “Паліном прыводны над або ягоная ступень няроўная 2”; адмаўленне выказвання “Сёння я пайду ў кіно ці на лекцыю па матэматычнай логіцы” раўназначнае выказванню “Сёння я не пайду ў кіно і не пайду на лекцыю па матэматычнай логіцы”. Выказванне “Калі я падрыхтуюся да экзамену, тады я атрымаю выдатную адзнаку” паводле практыкавання 5 (19) раўназначнае выказванню “Я не падрыхтуюся да экзамену ці атрымаю выдатную адзнаку”; выказванне “Калі функцыя непарыўная на адрэзку , тады яна абмежаваная на ” раўназначнае выказванню “Функцыя разрыўная на адрэзку ці абмежаваная на ”.

Сцверджанне 1. Калi i – таўталогii, тады – таўталогiя.

Доказ. Няхай i – таўталогii. Дапусцiм, што пры некаторым размеркаваннi логiкавых значэнняў для лiтараў, якiя ўваходзяць у i , набывае значэнне 0. Формула – таўталогiя, таму пры гэтых значэннях зменных набывае значэнне 1. Тады мае значэнне 0, а гэта супярэчыць таму, што – таўталогiя. ■

Сцверджанне 2 (правіла падстановы). Няхай ёсць формула, у якую ўваходзяць толькі літары , а атрымлiваецца з падстановай у прапазiцыйных формулаў замест адпаведна. Калі ╞ , тады ╞ , г.зн., падстанова ў таўталогiю дае таўталогiю.

Доказ сцверджання 2 пакідаем чытачу.

З сцверджання 2 вынікае, што ў практыкаваннях 4 і 5 можна лічыць не прапазіцыйнымі літарамі, а адвольнымі формуламі.

Сцверджанне 3. Няхай - формула, пабудаваная з прапазіцыйных літараў і іхніх адмаўленняў з дапамогаю толькі сымболяў логікавых аперацыяў і , - формула, атрыманая з заменай на , на і кожнай прапазіцыйнай літары (без адмаўлення) на і наадварот. Тады .

Доказ сцверджання 3 пакідаем чытачу (трэба скарыстаць законы дэ Моргана, падвойнага адмаўлення (гл. практыкаванне 5) і метад матэматычнай індукцыі).

Прыклад 8. Няхай ёсць , тады .

Практыкаванне 6. З дапамогаю сцверджання 3 знайсці формулы, раўназначныя адмаўленням наступных формулаў:

(1) ;

(2) ;

(3) .

Сцверджанне 4 (прынцып дваістасці (дуальнасці)). Няхай і – формулы таго ж выгляду, што ў сцверджанні 3, , – формулы, атрыманыя з і заменай на , на . Тады:

(а) Калі ╞ , тады ╞ ;

(b) Калі ╞ , тады ╞ ;

(c) Калі ╞ , тады ╞ ;

(d) Калі ╞ , тады ╞ .

Заўвага. Калі ў запісе формулаў , прапушчаныя дужкі паводле дамоўленасці, якую мы зрабілі пасля азначэння прапазіцыйнай формулы, тады перад выкананнем аперацыяў і ′ сцверджанняў 3 і 4 іх трэба аднавіць.

Доказ. (a) Няхай ╞ . Паводле сцверджання 3 , адсюль, відавочна, вынікае ╞ . Няхай – формула, атрыманая з падстановай замест літараў формулаў . Паводле сцверджання 2 ╞ . Паводле закону падвойнага адмаўлення (гл. практыкаванне 5) ; адсюль, відавочна, вынікае, што калі ў формуле выдаліць падвойныя адмаўленні перад кожнай прапазіцыйнай літарай (г.зн., перайсці да формулы ), тады атрымаецца таксама таўталогія.

Праілюструем доказ на наступным прыкладзе:

=

╞	╞
╞	╞
╞	╞
╞	╞

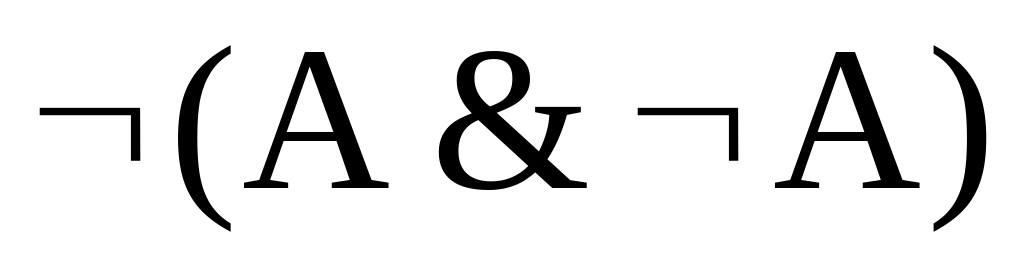
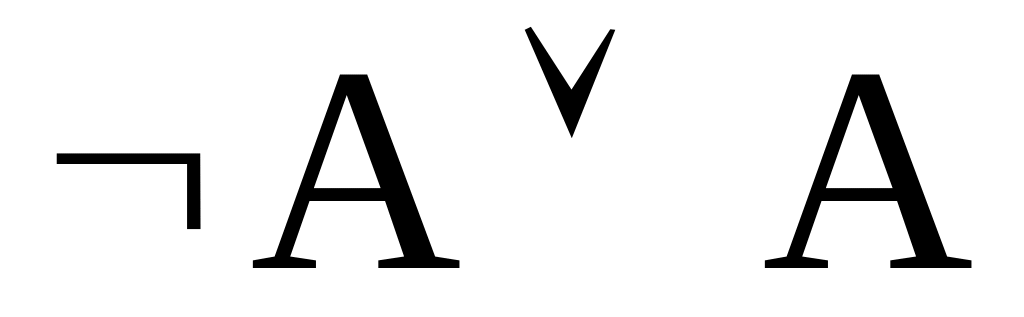
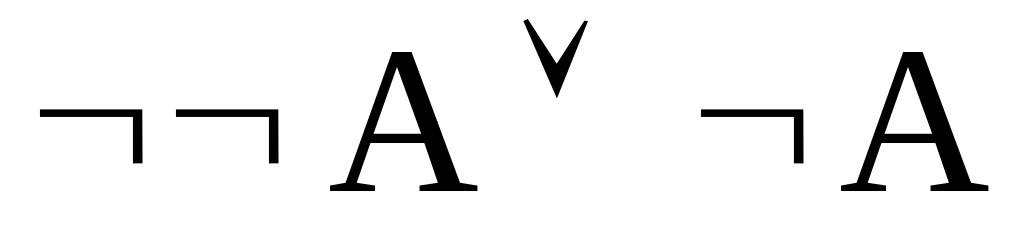
(b) Дапусцім, што ╞ . Адсюль, паводле закону падвойнага адмаўлення, відавочна, вынікае ╞ . Паводле сцверджання 3 ╞ , далей паводле сцверджання 2 ╞ і, паводле закону падвойнага адмаўлення, ╞ .

(c) Няхай ╞ . Відавочна, адсюль вынікае ╞ . Паводле сцверджання 3 ╞ . Паводле сцверджання 2 ╞ , адкуль ╞ .

Доказ сцверджання (d) пакідаем чытачу як практыкаванне. ■

Практыкаванне 7. З дапамогаю прынцыпу дуальнасці: (a) дакажыце логікавыя эквівалентнасці (3), (5), (7), (9), (11), (15) з практыкавання 5, скарыстаўшы (2), (4), (6), (8), (10), (14) з таго сама практыкавання;

(b) дакажыце, што прапазіцыйныя формулы (1), (8a), (8b) з практыкавання 4 ёсць таўталогіі, скарыстаўшы закон вылучанага трэцяга (прыклад 4) і (7a), (7b) з практыкавання 4.

Азначэнне. Прапазiцыйная формула называецца логiкавым вынiкам формулаў , калi для ўсiх набораў значэнняў лiтараў, што ўваходзяць у i , значэнне ёсць 1 усякi раз, калi значэнне кожнай формулы на гэтым наборы ёсць 1.

У гэтым выпадку будзем пiсаць ╞ .

Прыклад 9. ╞ , бо ў таблiцах праўдзiвасцi для гэтых формулаў ва ўсiх радках, дзе мае значэнне 1 (гэта першы i другi радкi), таксама мае значэнне 1:

1	1	1
1	1	0
0	1	1
0	0	0

Прыклад 10. Аналагiчна, ╞ , бо ў таблiцах праўдзiвасцi для гэтых формулаў ва ўсiх радках, дзе мае значэнне 1 (гэта першы i чацверты радкi), набывае значэнне 1:

1	1	1	1
1	0	0	0
0	0	1	1
0	1	0	1

Прыклад 11. ╞ , бо ў таблiцах праўдзiвасцi для гэтых формулаў у тых радках, дзе i набываюць значэнне 1 (гэта толькi першы радок), таксама мае значэнне 1:

1	1	1	1	1
1	1	0	0	0
0	0	1	1	1
0	0	1	0	0

Заўважым, што ╞ з’яўляецца больш моцным сцверджаннем, чым “Калі ╞ , тады ╞ ”.

Доказы наступных сцверджанняў вынікаюць з азначэння логікавага выніку, мы пакідаем іх чытачу як практыкаванне.

Няхай – формулы.

Сцверджанне 5. ╞ калi i толькi калi ╞ ( ). У прыватнасці, ╞ калi i толькi калi ╞ .

Сцверджанне 6. ╞ калi i толькi калi

╞ ( ).

Сцверджанне 7. ╞ калi i толькi калi ╞ ( ).

Прыклад 12. Цi правiльнае наступнае разважанне:

Сёння я пайду ў кiно на новую кiнакамедыю ці на заняткi па матэматычнай логiцы. Калi я пайду ў кiно на новую кiнакамедыю, тады я тры гадзiны буду смяяцца. Калi я пайду на заняткi па матэматычнай логiцы, тады я буду мець вялiкае задавальненне ад вывучэння логiкавых разважанняў. Значыць, сёння я тры гадзiны буду смяяца ці буду мець вялiкае задавальненне ад вывучэння логiкавых разважанняў.?

Каб адказаць на гэтае пытанне, абазначым выказванне “Я пайду ў кiно на новую кiнакамедыю” лiтарай , выказванне “Я пайду на заняткi па матэматычнай логiцы” – , “Я тры гадзiны буду смяяцца” – , “Я буду мець вялiкае задавальненне ад вывучэння логiкавых разважанняў” – . Тады ўмовы нашага разважання запiшуцца формуламi

. (1)

Для таго, каб высветлiць, цi правiльнае нашае разважанне, мы мусiм праверыць, цi будуць гэтыя формулы мець логiкавым вынiкам формулу . Дапусцiм, што формула не ёсць логiкавы вынiк формулаў (1). Тады пры некаторых значэннях лiтараў кожная з формулаў (1) набывае значэнне 1, а формула – значэнне 0:

.

З таго, што , маем . З вынікае ; а з – . Але тады . Атрыманая супярэчнасць паказвае, што формула ёсць логiкавы вынiк формулаў (1) i, значыць, нашае разважанне правiльнае.

Прыклад 13. Калi заўтра будзе дождж, тады я пайду на спатканне, калі куплю парасон. Я змагу купіць парасон толькі калі буду мець грошы. Заўтра будзе дождж, але я не буду мець грошаў. Значыць, я не пайду на спатканне.

Каб прааналізаваць гэтае разважанне, абазначым выказванне “Заўтра будзе дождж” праз , “Я пайду на спатканне” – , “Я куплю парасон” – , “Я буду мець грошы” – . Умовы нашага разважання запішуцца формуламі

, (2)

а выснова – формулай . Трэба высветліць, ці будзе гэтая формула логікавым вынікам папярэдніх. Паспрабуем падабраць значэнні літараў такім чынам, каб усе формулы (2) набывалі значэнне 1, а – 0. З атрымаем , тады формула мае значэнне 1 пры адвольных значэннях і ; з вынікае , а адсюль і з будзем мець . Такім чынам, мы змаглі падабраць логікавыя значэнні літараў, пры якіх формулы (2) маюць значэнні 1, а – 0; значыць, апошняя формула не ёсць логікавы вынік формулаў (2), і нашае разважанне няправільнае. (У выпадку, калі будзе дождж, я не буду мець грошаў, не куплю парасон, але я пайду на спатканне, бо каханне мацнейшае за ўсе гэтыя неспрыяльныя абставіны.)

Практыкаванне 8. Для кожнай з наступных прапазiцыйных формулаў напiсаць поўную i скарочаную таблiцы праўдзiвасцi i высветлiць, цi з’яўляецца яна таўталогiяй, супярэчнасцю альбо нi тым, нi iншым:

(1) ;

(2) ;

(3) ;

(4) ;

(5) ;

(6)

(7) ;

(8) ;

(9) ;

(10) ;

(11) ;

(12) ;

(13) ;

(14) ;

(15) .

Практыкаванне 9. Запiсаць наступныя выказваннi ў выглядзе прапазiцыйных формулаў, скарыстаўшы лiтары для абазначэння элементарных выказванняў:

(1) З таго, што 120 дзелiцца на 2 i на 3, а 2 i 3 узаемна простыя, вынікае, што 120 дзелiцца на 6.

(2) З таго, што 10 - просты лiк i вынiкае, што 10 – няцотны лiк.

(3) Студэнт не можа вучыцца, калi ён стамiўся, адчувае незадаволенасць жыццём ці галодны.

(4) Непарыўнасць функцыi на ёсць дастатковая ўмова iнтэгравальнасцi функцыi на гэтым адрэзку.

(5) Непарыўнасць функцыi на ёсць неабходная ўмова дыферэнцавальнасцi функцыi на гэтым адрэзку.

(6) Для таго, каб Васiль атрымаў выдатную адзнаку, неабходна, каб ён падрыхтаваўся да экзамену i не хваляваўся.

(7) Калi ў краiне будзе ўсталяваная дыктатура, тады яна стане мiлiтарысцкай дзяржавай i трапіць у мiжнародную iзаляцыю, а народ канчаткова збяднее.

(8) Калi Ян будзе трэнiравацца i будзе мець грошы, ён паедзе ў Гiмалаi, а калi не будзе мець грошаў, тады будзе працаваць на будоўлi.

(9) Для таго, каб палiном меў рэчаiсны корань, неабходна, каб ён дзялiўся на ці меў неадмоўны дыскрымiнант.

(10) Марыяна ці пойдзе на спатканне з сынам, i тады вымушана будзе хлусiць, ці будзе адчуваць сябе нешчаслiвай.

(11) Для таго, каб Стась стаў матэматыкам, дастаткова, каб ён слухаў лекцыi, чытаў кнiгi па матэматыцы i кожны дзень развязваў задачы.

(12) Каб здаць экзамен па матэматычнай логіцы на “выдатна”, неабходна перад экзаменам добра выспацца.

(13) Каб здаць экзамен па матэматычнай логіцы на “выдатна”, дастаткова перад экзаменам добра выспацца.

(14) Немагчыма стаць матэматыкам, калі не будзеш сур’ёзна працаваць, не навучышся самастойна думаць і не будзеш мець багатую фантазію.

(15) Я пайду на заняткі па матэматычнай логіцы, калі прачытаю ўсе лекцыі.

(16) Я пайду на заняткі па матэматычнай логіцы толькі калі прачытаю ўсе лекцыі.

Практыкаванне 10. Запісаць у выглядзе кан’юнкцыі ці дыз’юнкцыі ўмовы праўдзівасці наступных сказаў ( і – рэчаісныя лікі):

(1) ;

(2) ;

(3) ;

(4) ;

(5) ;

(6) ;

(7) ;

(8) ;

(9) .

Практыкаванне 11. Высветлiць, цi з’яўляецца прапазiцыйная формула логiкавым вынiкам папярэднiх формулаў:

(1) ╞ ;

(2) ╞ ;

(3) ╞ ;

(4) ╞ ;

(5) ╞ ;

(6) ╞ ;

(7) ╞ ;

(8) ╞ ;

(9) ╞ ;

(10) ╞ .

Практыкаванне 12. Цi правiльныя наступныя разважаннi? Спачатку адкажыце на гэтае пытанне з дапамогаю логiкi, якою вы карыстаецеся пры вывучэннi матэматыкi i ў штодзённым жыццi (логiкi даследчыка), а затым праверце сябе: запiшыце разважаннi з дапамогаю прапазіцыйных формулаў i высветлiце, цi з’яўляецца апошнi сказ логiкавым вынiкам папярэднiх.

(1) Калi 3 i 5 – простыя лiкi, тады яны простыя лiкi–блiзняты. Лiкi 7 i 11 – простыя. Значыць, 7 i 11 – простыя лiкi–блiзняты.

(2) Або Вiктар i Ян браты, або яны аднакурснiкi. Калi Вiктар i Ян браты, тады Сяргей i Ян не браты. Калi Вiктар i Ян аднакурснiкi, тады Ян i Мiхась таксама аднакурснiкi. Значыць, або Сяргей i Ян не браты, або Ян i Мiхась аднакурснiкi.

(3) Калi Васiль не сустракаў Яна, тады або Ян не быў на лекцыях, або Васiль манiць. Калi Ян быў на лекцыях, тады Васiль сустракаў Яна, i Сяргей быў у чытальнi пасля лекцыяў. Калi Сяргей быў у чытальнi пасля лекцыяў, тады або Ян не быў на лекцыях, або Васiль манiць. Значыць, Ян не быў на лекцыях.

(4) Калi 6 – складовы лiк, тады 12 – складовы лiк. Калi 12 – складовы лiк, тады iснуе просты лiк, большы за 12. Калi iснуе просты лiк, большы за 12, тады iснуе складовы лiк, большы за 12. Калi 6 дзелiцца на 2, тады 6 – складовы лiк. Лiк 12 складовы. Значыць, 6 – складовы лiк.

(5) Калi Тамара не будзе ўлетку падарожнiчаць на байдарцы, тады яна будзе адчуваць сябе нешчаслiвай. Калi Тамара будзе адчуваць сябе нешчаслiвай, тады Казiмiр будзе галодны. Калi Казiмiр не будзе палiваць гуркi, тады ўзiмку ён будзе есцi толькi бульбу. Калi Тамара будзе падарожнiчаць на байдарцы, тады i Казiмiр будзе. Значыць, для таго каб не быць галодным i есцi не толькi бульбу, Казiмiру неабходна пайсцi ў падарожжа на байдарцы i палiваць гуркi.

(6) Калi ён гэта сказаў, тады ён дурань ці беспрынцыпны. Ён не дурань i не пазбаўлены прынцыпаў. Значыць, ён не казаў гэтага.

(7) Калi б ён ёй не сказаў, яна нiколі не даведалася б. А не запыталася б яна ў яго, ён бы i не сказаў ёй. Але яна даведалася. Значыць, яна ў яго запыталася.

(8) Калi

(3)

тады . Але калi i толькi калi , што будзе калi i толькi калi або . Значыць, толькi –6 i –1 могуць быць каранямi раўнання (3), г.зн., з вынiкае або .

(9) Тое, што i (8), з заменай высновы на “значыць, –6 i –1 – каранi раўнання (3), г.зн., з вынiкае i з вынiкае ”.

(10) Калi Уладзiмер – камунiст, тады Уладзiмер – атэiст. Уладзiмер – атэiст. Значыць, Уладзiмер – камунiст.

(11) Калi курс матэматычнае логiкi нецiкавы, тады ён карысны. Калі курс матэматычнае логiкi няпросты, тады ён цікавы ці бескарысны. Курс матэматычнае логiкi цікавы ці няпросты. Значыць, гэты курс цiкавы.

(12) У краіне можа быць развітая адукацыя толькі калі яна дэмакратычная і ў ёй высокі ўзровень развіцця матэматыкі. Калі ў краіне не развітая адукацыя, тады ў ёй не можа быць высокага ўзроўню развіцця матэматыкі. Калі краіна дэмакратычная, тады ў ёй развітая адукацыя. Значыць, краіна дэмакратычная калі і толькі калі ў ёй высокі ўзровень развіцця матэматыкі.

(13) Калі заўтра будзе мароз, тады я апрану футра, калі прышыю гузік. Заўтра будзе мароз, але гузік я не прышыю Значыць, я не апрану футра.

(14) Калі заўтра будзе мароз, тады я апрану футра, калі прышыю гузік. Заўтра не будзе марозу і я не прышыю гузік. Значыць, я не апрану футра.

(15) Калі заўтра будзе мароз, тады я апрану футра, калі прышыю гузік. Заўтра не будзе марозу, а гузік я прышыю. Значыць, я не апрану футра.

(16) Калі заўтра будзе мароз, тады я апрану футра, калі прышыю гузік. Заўтра не будзе марозу, а гузік я прышыю. Значыць, я апрану футра.

(17) Для таго, каб захаваць жыццё на Зямлі, неабходна ўкладаць грошы ў экалогію. Людзі змогуць укладаць грошы ў экалогію толькі калі яны абмяжуюць свае патрэбы. Калі людзі будуць абмяжоўваць свае патрэбы і лічыць выхаванне любові і павагі да ўсяго жывога найгалоўнай задачай, тады яны будуць укладаць грошы ў экалогію. Людзі або будуць лічыць выхаванне любові і павагі да ўсяго жывога найгалоўнай задачай, або не будуць абмяжоўваць свае патрэбы. Калі людзі будуць лічыць выхаванне любові і павагі да ўсяго жывога найгалоўнай задачай, тады жыццё на Зямлі захаваецца. Значыць, для таго, каб захавалася жыццё на Зямлі, людзям неабходна і дастаткова лічыць выхаванне любові і павагі да ўсяго жывога найгалоўнай задачай і ўкладаць сродкі ў экалогію.

Практыкаванне 13. Махатма Гандзi ў адной з сваiх прамоваў сказаў: “Калi я не буду ўдзельнiчаць у дэманстрацыях пратэсту, тады дэмакратычная апазiцыя будзе слабая або дыктатар застанецца пры ўладзе. Для таго, каб дыктатар не быў пры ўладзе, трэба, каб дэмакратычная апазiцыя была моцная. Калi дыктатар будзе пры ўладзе, тады Iндыя застанецца калонiяй Брытанскай iмперыi i не будзе нейтральнай дзяржавай. Калi Iндыя застанецца калонiяй Брытанскай iмперыi або не будзе нейтральнай дзяржавай, тады iндусы будуць ваяваць у чужых краiнах. Значыць, для таго, каб iндусы не ваявалi ў чужых краiнах, мне трэба ўдзельнiчаць у дэманстрацыях пратэсту”.

Цi меў Махатма Гандзi рацыю з пункту гледжання матэматычнае логiкi?

Практыкаванне 14. Браўн, Джонс i Смiт абвiнавачваюцца ў падробцы звестак пра даходы, што падлягаюць падатковаму абкладанню. Яны даюць наступныя паказаннi:

Браўн: Джонс вiнаваты, а Смiт невiнаваты.

Джонс: Калi Браўн вiнаваты, тады вiнаваты i Смiт.

Смiт: Я невiнаваты, але прынамсi адзiн з iх дваiх вiнаваты.

(a) Цi супольныя паказаннi ўсiх трох падазраваных (г.зн., цi могуць яны быць праўдзiвымi адначасова)?

(b) Паказаннi аднаго з падазраваных вынiкаюць з паказанняў другога; пра чые паказаннi iдзе гаворка?

(c) Калi ўсе трое невiнаватыя, тады хто схлусiў?

(d) Дапусціўшы, што паказаннi ўсiх падазраваных праўдзiвыя, вызначце, хто вiнаваты i хто невiнаваты?

(e) Калi невiнаваты гаворыць праўду, а вiнаваты хлусiць, тады хто вiнаваты i хто невiнаваты?

У гэтым раздзеле мы вывучаем логiку з двума значэннямi праўдзiвасцi: праўда (1) i няпраўда (0). Часам разглядаюць трохзначную логiку з значэннямi праўдзiвасцi праўда, нявызначанасць i няпраўда, якiя абазначаюць 2, 1 i 0 адпаведна, з аперацыямi , , , , азначанымi наступнымi таблiцамi:

2	1		2	2	2		2	2	2		2	2	2
1	0		2	1	1		2	1	2		2	1	1
0	2		2	0	0		2	0	2		2	0	0
			1	2	1		1	2	2		1	2	1
			1	1	1		1	1	1		1	1	1
			1	0	0		1	0	1		1	0	1
			0	2	0		0	2	2		0	2	2
			0	1	0		0	1	1		0	1	2
			0	0	0		0	0	0		0	0	2

Гэтыя аперацыi можна задаць формуламi:

, ,

, ,

дзе праз абазначана логiкавае значэнне , – цэлая частка лiку .

У гэтай логiцы, у адрозненне ад дзвюхзначнай, закон вылучанага трэцяга несапраўдны; замест яго праўдзiвы закон вылучанага чацвертага .

Iснуюць таксама шматзначныя логiкi, у якiх ( — адвольны натуральны лiк) “значэнняў праўдзiвасцi”.