
Теоретическая часть
Рассмотрим элементарные булевы функции
определенные на множестве
![]() и опишем их как некоторые нестандартные
функции произвольного алгоритмического
языка:
и опишем их как некоторые нестандартные
функции произвольного алгоритмического
языка:
Дизъюнкция:
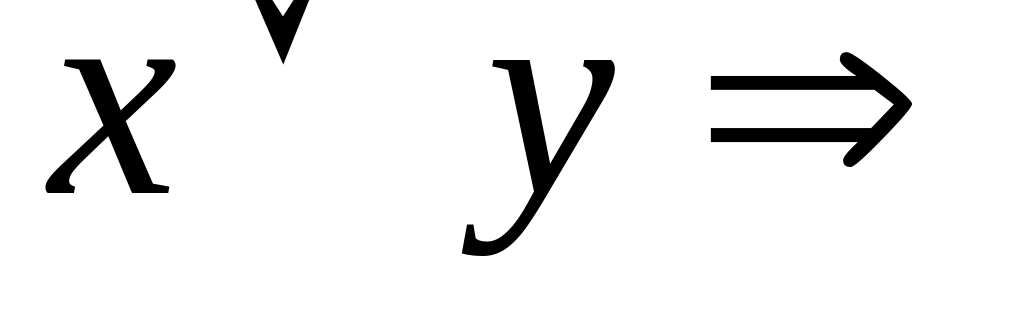 Diz(x,y): if (x=0) and (y=0) then 0
else 1;
Diz(x,y): if (x=0) and (y=0) then 0
else 1;Конъюнкция:
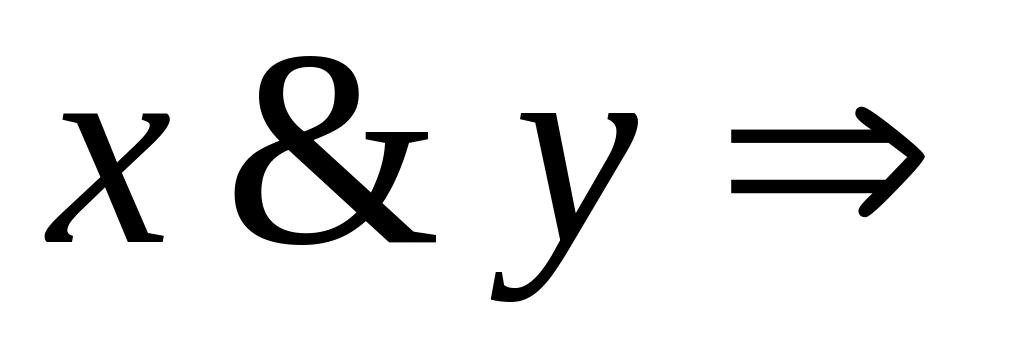 Kon(x,y): if (x=1) and (y=0) then 1
else 0;
Kon(x,y): if (x=1) and (y=0) then 1
else 0;Отрицание:
 Ne(x): if (x=0) then 1 else 0;
Ne(x): if (x=0) then 1 else 0;Импликация:
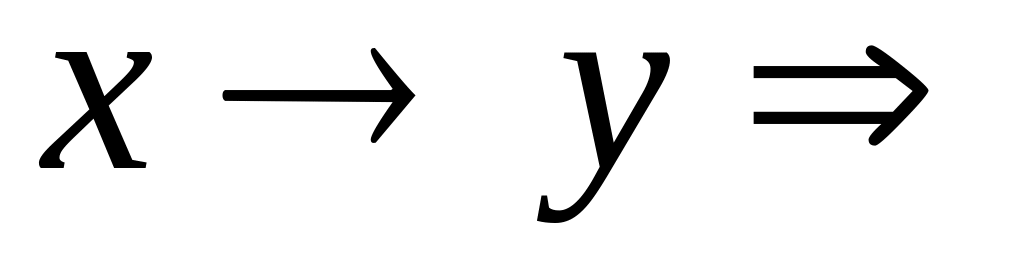 Imp(x,y): if (x=1)
and (y=0) then 0 else 1;
Imp(x,y): if (x=1)
and (y=0) then 0 else 1;Сумма по модулю 2:
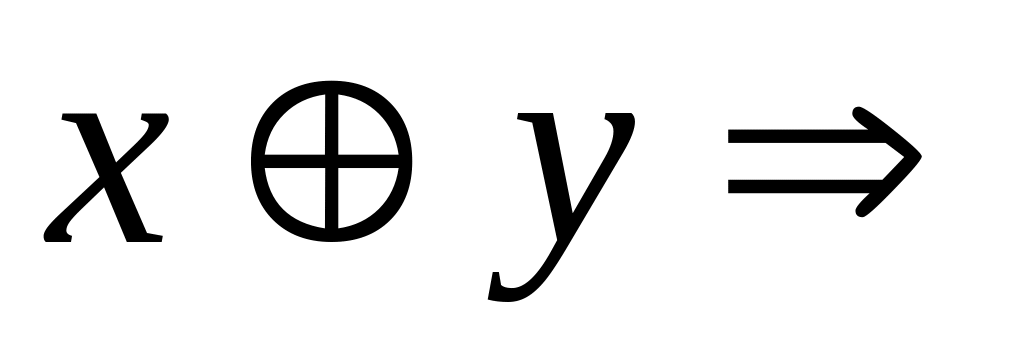 Mod2(x,y): if ((x=0) and (y=1)) or
((x=1) and (y=0)) then 1 else 0;
Mod2(x,y): if ((x=0) and (y=1)) or
((x=1) and (y=0)) then 1 else 0;Эквивалентность:
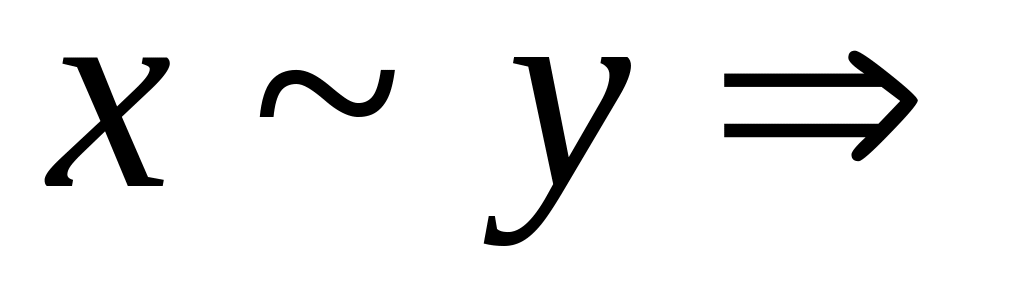 Akv(x,y): Ne(Mod2(x,y));
Akv(x,y): Ne(Mod2(x,y));Штрих Шеффера:
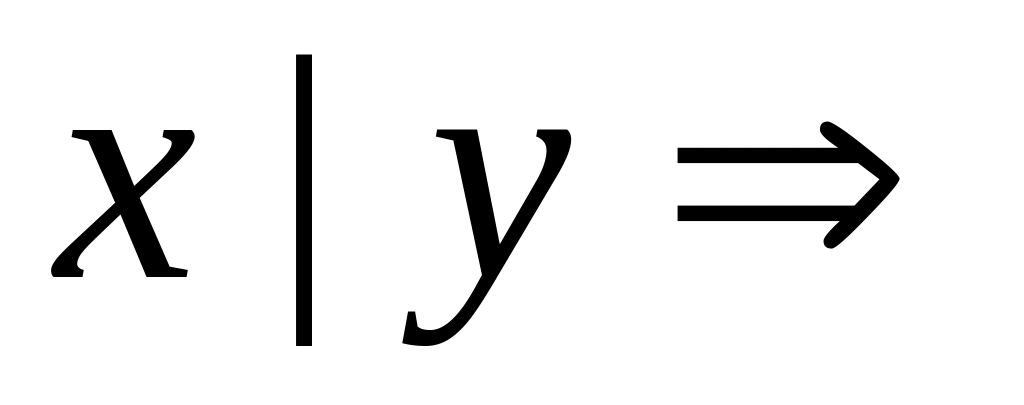 Sheff(x,y):
Ne(Kon(x,y));
Sheff(x,y):
Ne(Kon(x,y));Стрелка Пирса:
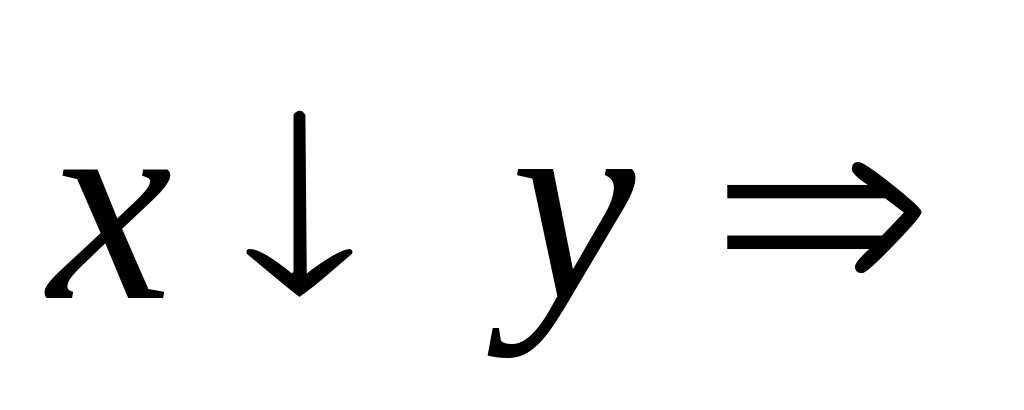 Pirs(x,y):
Ne(Diz(x,y)).
Pirs(x,y):
Ne(Diz(x,y)).
Формулой над множеством
![]() называется всякое (и только такое)
выражение вида:
называется всякое (и только такое)
выражение вида:
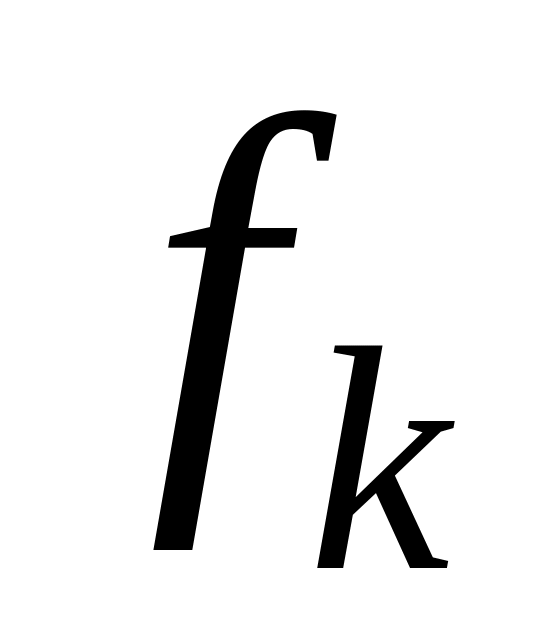 и
и
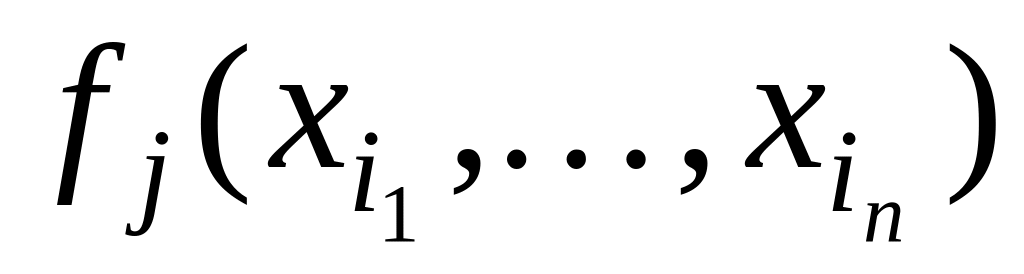 ,
где
- нуль-местный, а
,
где
- нуль-местный, а
 - n-местный функциональные
символы и
- n-местный функциональные
символы и
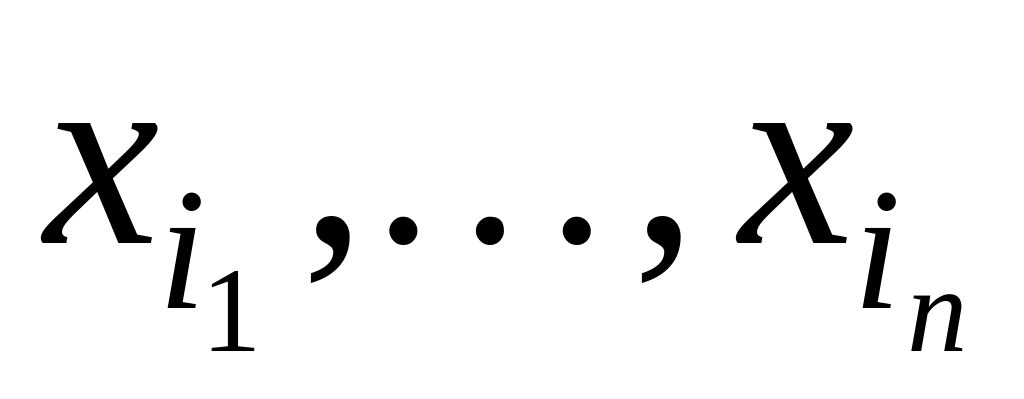 - переменные их множества
- переменные их множества
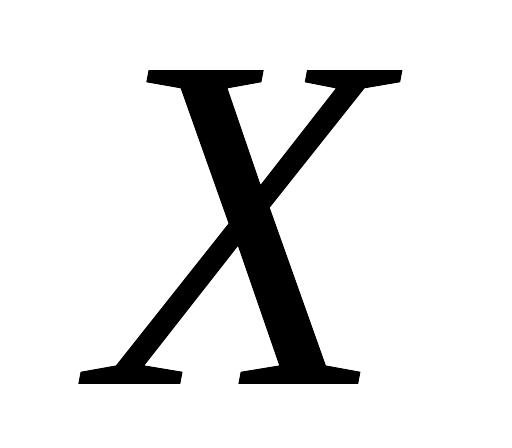 .
.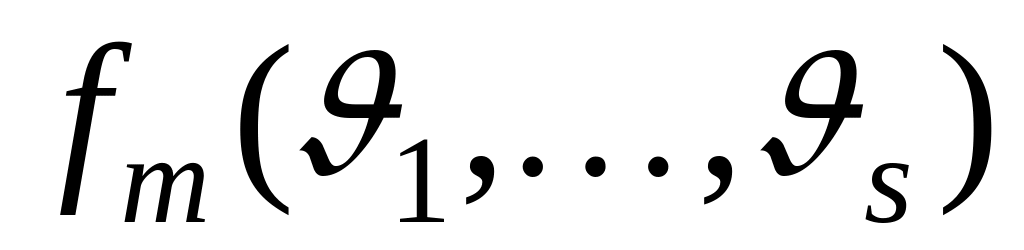 ,
где
,
где
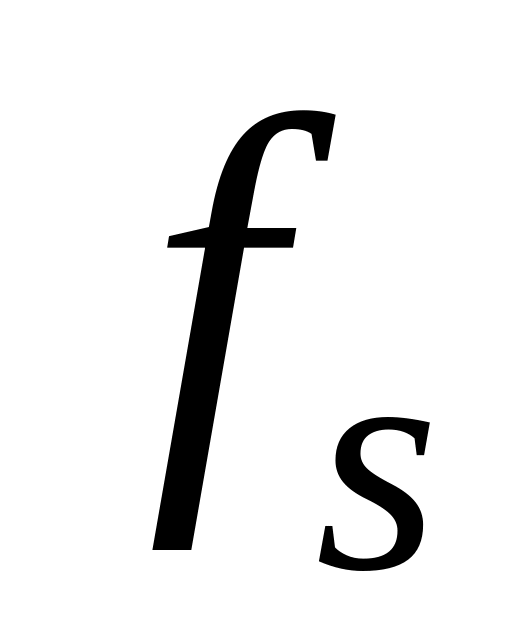 - s-местный функциональный
символ и
- s-местный функциональный
символ и
 ,
,
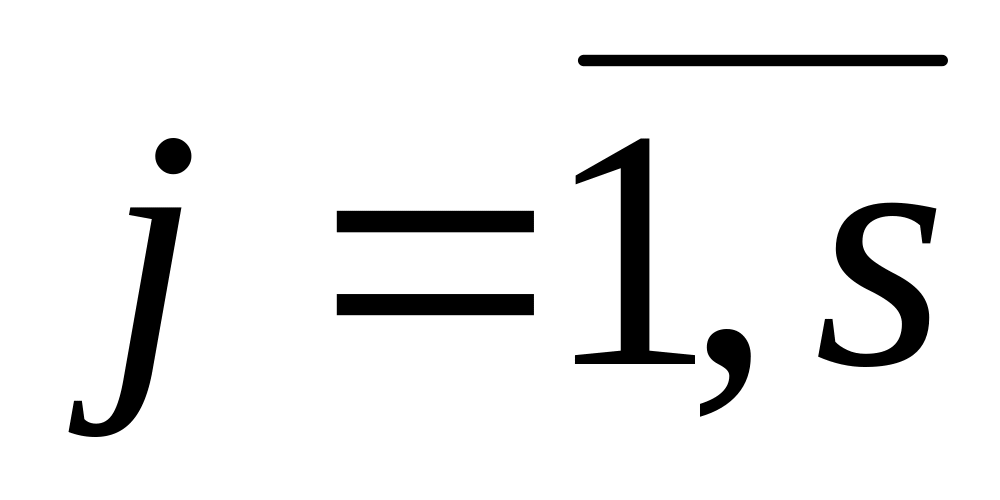 - либо формула над
,
либо переменная из
.
- либо формула над
,
либо переменная из
.
Пусть заданы на множестве булевых
функций заданы две формулы
![]() и
и
![]() .
.
Понятие функции
![]() ,
реализуемой формулой
над множеством связок
,
реализуемой формулой
над множеством связок
![]() ,
вводится следующим образом:
,
вводится следующим образом:
формуле
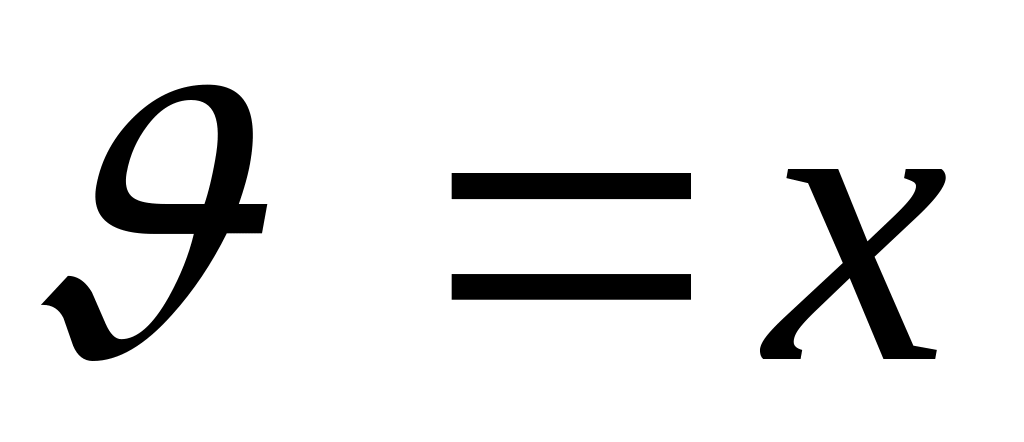 ,
где
,
где
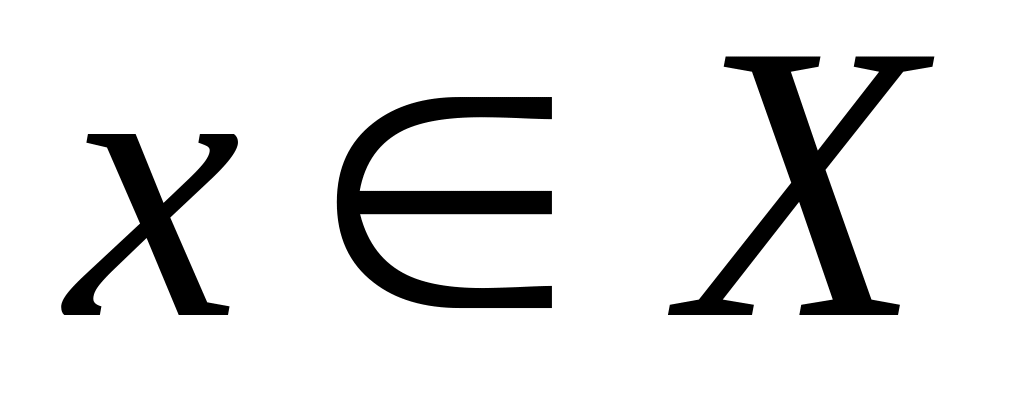 ,
сопоставляется тождественная функция
,
сопоставляется тождественная функция
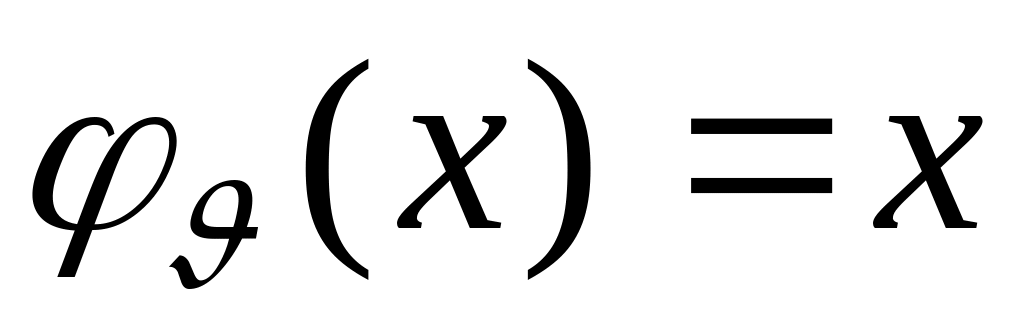 ;
;если
 (или
(или
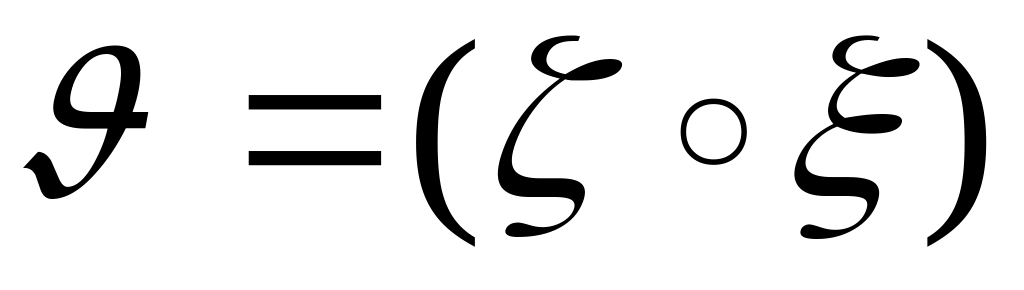 ,
где
,
где
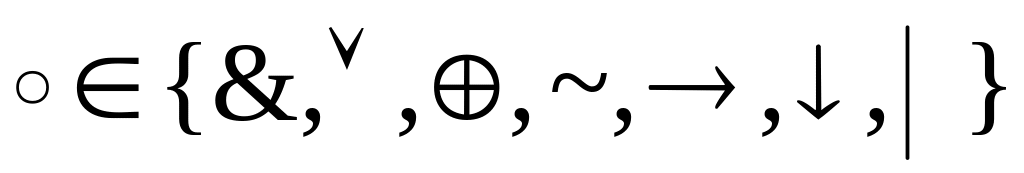 ),
то
),
то
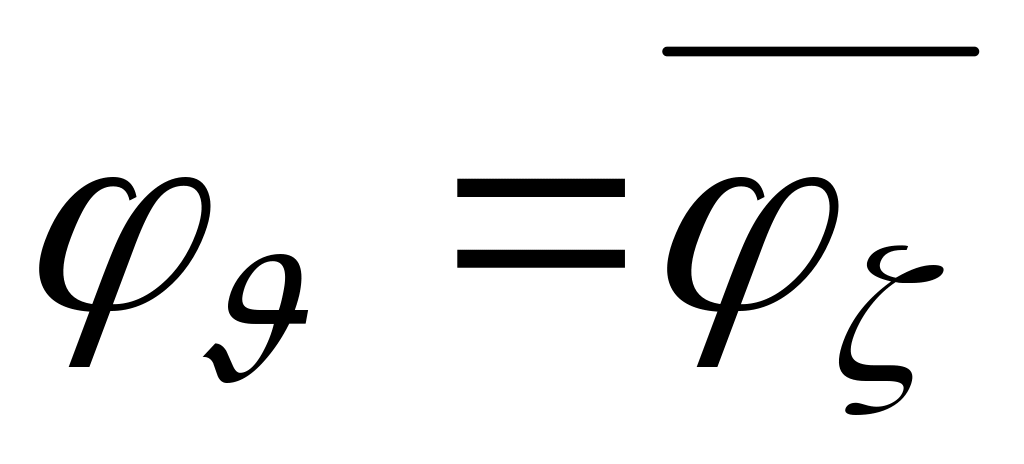 (соответственно
(соответственно
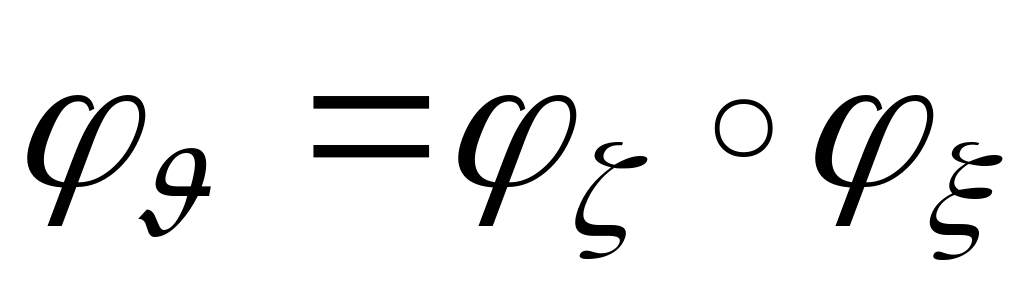 ,
где символ
,
где символ
 надо понимать уже как обозначение для
соответствующей элементарной булевой
функции).
надо понимать уже как обозначение для
соответствующей элементарной булевой
функции).
Пусть
![]() - множество тех переменных, которые
встречаются хотя бы в одной их формул
или
.
Формулы
и
называются эквивалентными (обозначение:
- множество тех переменных, которые
встречаются хотя бы в одной их формул
или
.
Формулы
и
называются эквивалентными (обозначение:
![]() ),
если на всяком наборе
),
если на всяком наборе
![]() значений переменных
значений переменных
![]() значения функций
значения функций
![]() и
и
![]() ,
реализуемых соответственно формулами
и
,
совпадают.
,
реализуемых соответственно формулами
и
,
совпадают.
Лабораторная работа состоит в построении двух формул на классе булевых функций и проверке их тождественности.
Входные параметры: матрица размерности
![]() всех различных наборов значений
переменных и две формулы, реализующие
булевы функции
переменных.
всех различных наборов значений
переменных и две формулы, реализующие
булевы функции
переменных.
Выходные параметры:
![]() ,
если заданные формулы неэквивалентны
и
,
если заданные формулы неэквивалентны
и
![]() ,
если заданные формулы эквивалентны.
,
если заданные формулы эквивалентны.
Указания к выполнению лабораторной работы
Построить матрицу, реализующую все различные наборы значений переменных. Построение может быть основано на принципе записи десятичных чисел в двоичных кодах или вестись по столбцам матрицы, учитывая, что в последнем столбце 0 чередуется с 1 через одну строку, во втором столбце – через две строки, в третьем – через четыре строки и т.д. Алгоритм, выполняющий данное построение, должен быть записан в виде процедуры (
 )
или программного модуля (
)
или программного модуля ( ).
Замечание: алгоритм должен быть
построен для n
переменных, где n –
любое натуральное число, задаваемое с
экрана.
).
Замечание: алгоритм должен быть
построен для n
переменных, где n –
любое натуральное число, задаваемое с
экрана.Реализовать приведенные выше булевы функции. Алгоритм оформить в виде функций (
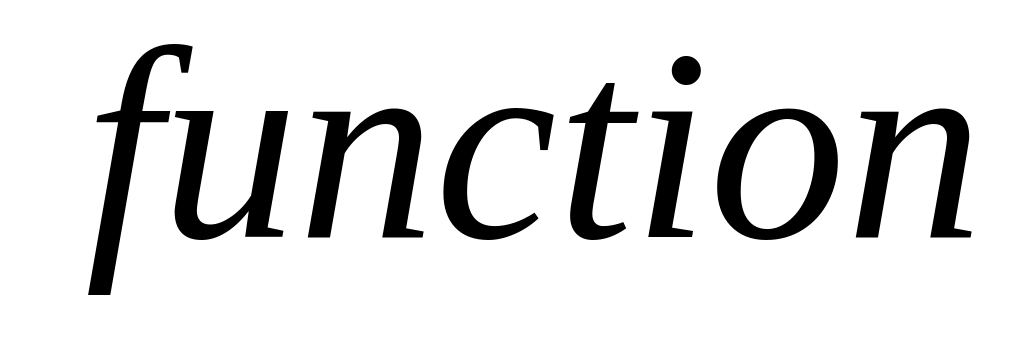 ).
).Записать указанные в задании формулы с помощью построенных функций (например, запись
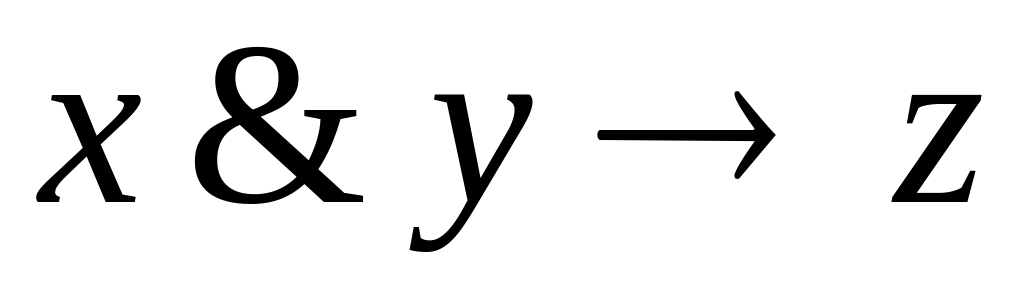 примет следующий вид: Imp(Kon(x,y),z)).
примет следующий вид: Imp(Kon(x,y),z)).Продвигаясь в цикле по строкам матрицы, вычислить значения функций, реализованных заданными формулами, на каждом наборе.
Сравнить в цикле полученные вектора
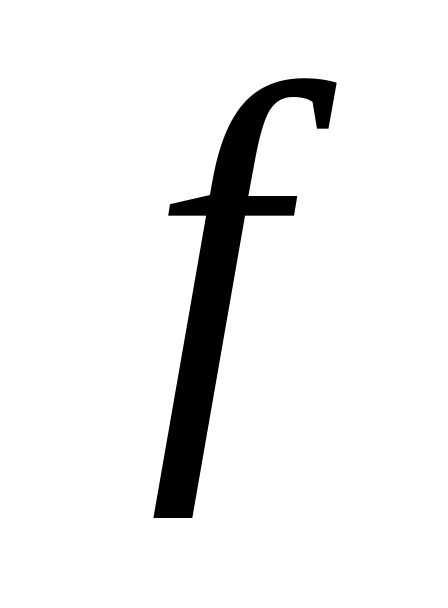 и
и
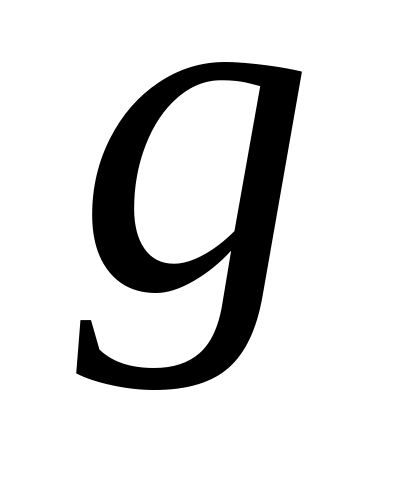 .
Результат сравнения
,
если полученные вектора различны и
,
если полученные вектора равны между
собой.
.
Результат сравнения
,
если полученные вектора различны и
,
если полученные вектора равны между
собой.
Варианты заданий
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
;
![]() ;
;
![]() ;
;
![]() .
.
Лабораторная работа № 3.
Построение и быстрое вычисление совершенной ДНФ.
Постановка задачи. Методом элементарных преобразований построить совершенную ДНФ, вычислить ее значение с помощью «быстрого» алгоритма и записать совершенную ДНФ по таблице истинности.
