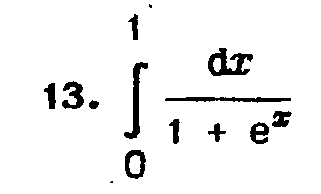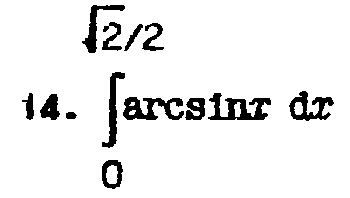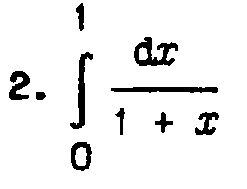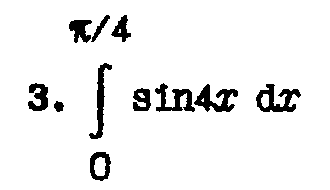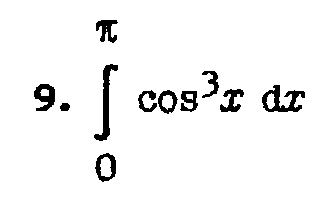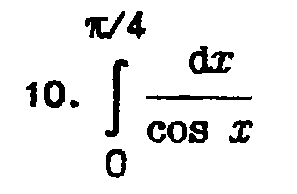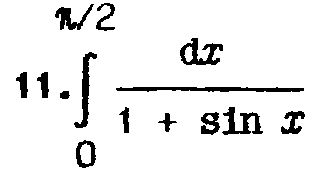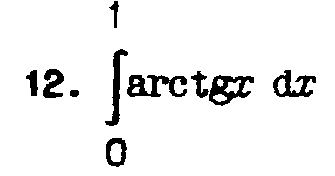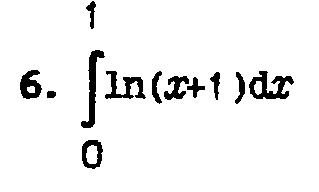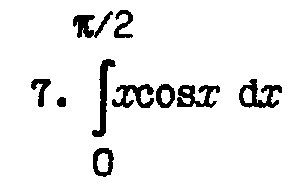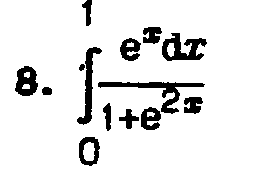4.1.2 Алгоритм прямоугольников-трапеций

Алгоритм прямоугольников-трапеций вычисления интеграла с заданной точностью выглядит следующим образом:

1. Полагаем

2. Находим

3. Вычисляем

4. Сравниваем с ε.

Если > ε, то полагаем n=2n; H=h;

и возвращаемся к п. 2.

5. Вычисляем

и принимаем

4.2 Задание к работе

Дан интеграл.

Варіант		Варіант		Варіант		Варіант
1		2		3		4
5		6		7		8
9		10		11		12
13		14		15			16

1. Вычислить заданные интегралы по формулам прямоугольников, трапеций и Симпсона, если отрезок интегрирования разбит на n=6 и n=8 частей.

2. Оценить погрешность результата. Результаты вычислений представить в виде таблицы приведенной в примере теоретической части лабораторной работы.

3. Составить блок-схему алгоритма и программу вычислений интегралов по методу прямоугольников-трапций с оценкой точности вычисления по правилу Рунге. Вычислить интеграл с точностью =10^-5.

Лабораторная работа №5 Численное дифференцирование

Цель работы - изучить конечноразностные формулы численного дифференцирования.

5.1 Краткие теоретические сведения

5.1.1 Вычисление производной по ее определению

Пусть функция у=f(х) определена в некоторой окрестности точки х₀ и имеет производную в этой точке, т.е. существует предел отношения приращения функции к приращению аргумента при стремлении к нулю:

(1)

Значение производной в точке х₀ можно получить, переходя к пределу в (1) по последовательности целых чисел п и полагая, например, .Здесь -некоторое начальное приращения аргумента, а - некоторое число, больше единицы, Тогда значение производной функции f(х) в точке запишется так :

Отсюда получаем приближенное равенство

(2)

Для функции у=f(х), имеющей непрерывную производную до второго порядка включительно в окрестности точки х₀, точность приближения производной соотношением (2) можно установить, воспользовавшись формулой Тейлора

Тогда

и окончательно имеем

Для достижения заданной точности приближения производной при определённом числе вычислений можно использовать неравенство

(3)

Пример. Вычислить производную функции y=sinx в точке с точностью ( ).

Решение. Положим , откуда

Определим приближенное значение производной

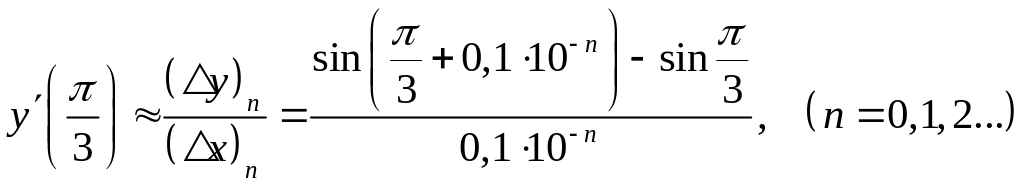
Найдем отношения, аппроксимирующие производную:

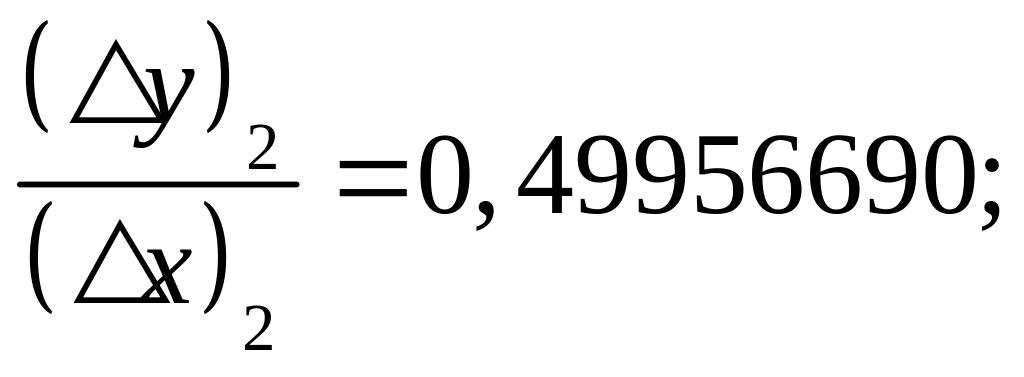
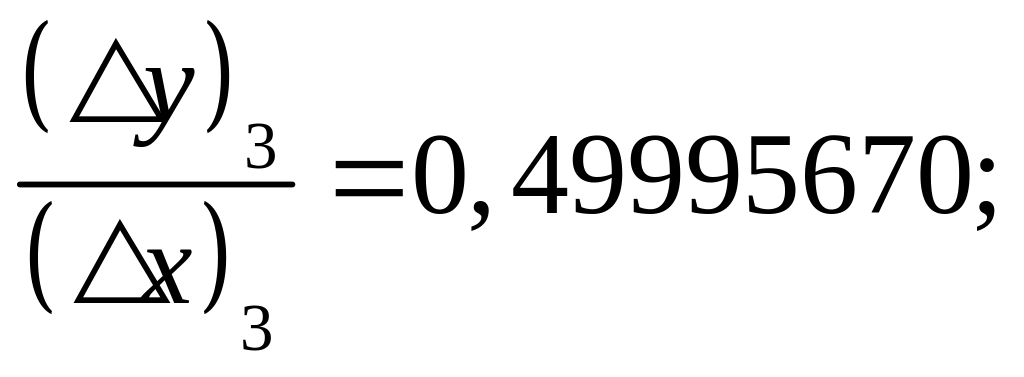
Итак, начиная с третьего приближения, в соответствии с оценкой (3) получаем искомое приближение производной данной функции с точностью, не меньше, чем заданная