4.5.2. Устройства на операционном усилителе
Рассмотренная в предыдущем разделе схема включения операционного усилителя (ОУ) может суммировать и вычитать напряжения, интегрировать, дифференцировать и логарифмировать входные сигналы и выполнять ряд других операций.
Рассмотрим некоторые из них.
а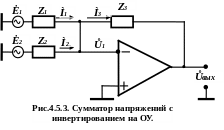
)
Сумматор с инвертированием
(рис.4.5.3)
Для этой схемы справедливы соотношения
,
а
.
Тогда уравнение (4.5.16) примет вид:
. (4.5.17)
б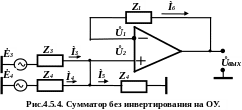
)
Сумматор без инвертирования (рис.4.5.4)
Для этой схемы справедливы соотношения
,
а
.
Тогда уравнение (4.5.16) примет вид:
. (4.5.18)
в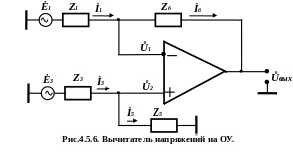
).
Вычитатель (рис.4.5.5).
Для этой схемы справедливы соотношения
,
а
.
Тогда уравнение (4.5.16) примет вид:
. (4.5.19)
г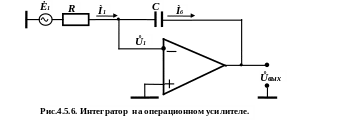
)
Интегратор (рис.4.5.6)
Для этой схемы справедливы соотношения
,
а
.
Тогда уравнение (4.5.16) примет вид:
,
(4.5.20)
а передаточная характеристика в комплексном виде примет вид
. (4.5.20)
Выражение (4.5.20) описывает передаточную характеристику в комплексном виде идеальную интегрирующую цепь (см. раздел “Синтез интегрирующих цепей”).
д) Дифференциатор (рис.4.5.7)
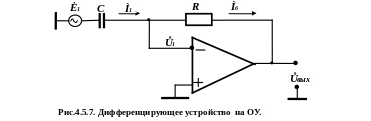
Для этой схемы справедливы соотношения
,
,
а
.
Тогда уравнение (4.5.16) примет вид:
,
(4.5.21)
а передаточная характеристика в комплексном виде примет вид
. (4.5.22)
Выражение (4.5.20) описывает передаточную характеристику в комплексном виде идеальную дифференцирующую цепь (см. раздел “Синтез дифференцирующих цепей”).
е) Логарифмирующее устройство (рис.4.5.8)
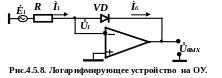
Для этой схемы справедливы соотношения
,
,
а
,
а роль
выполняет диоды с плоскостным p
– n переходом.
Известно, что вольтамперная характеристика p – n перехода описывается равенством
, (4.5.23)
где
,
k - постоянная
Больцмана, Т – абсолютная
температура, q
– заряд электрона,
падение напряжения на диоде, μ близко
к единице. . При комнатной температуре
.
Логарифмируя (4.5.23), получаем
. (4.5.24) Ток
через сопротивление R,
являющийся также и током через диод,
при условии малого сопротивления
открытого диода и малого выходного
сопротивления операционного усилителя
и 
. (4.5.25) По
второму закону Кирхгофа
(4.5.26)
или 
,
Тогда выходное напряжение будет связано с входным выражением
. (4.5.27)
Суммируя выходные напряжения нескольких логарифмических усилителей, можно получить сумму логарифмов от нескольких напряжений, равную логарифму произведения этих напряжений.