1). Преобразование исследуемой характеристики цепи к билинейной форме (4.3.9).
2). Определение функции чувствительности по заданному параметру.
3). Анализ функции чувствительности в соответствии с поставленной задачей.
Пример.
Пусть задана электронная цепь, которая описывается комплексной частотной характеристикой следующего вида
,
где К – статический коэффициент усиления активного прибора (например, транзистора).
Определить:
частоту, на которой относительное изменение коэффициента усиления приводит к максимальному относительному отклонению АЧХ;
величину этого отклонения при отклонении коэффициента усиления на 1% (δK=0,01);
допустимое отклонение коэффициента усиления при условии δT(ω)=0,03.
Решение
Приводим комплексную частотную характеристику к билинейной относительно коэффициента усиления к форме
.
2. Определяем функцию чувствительности
.
Находим чувствительность АЧХ,
как вещественную часть
3. Построив график
,
определяем, что максимальное отклонение
δТ(ω) имеет место при ω=1 (
)
и в соответствии с (4.3.12) при δК=0,01 равно
.
Допустимое отклонение δК при заданном
δТ(ω)=0,03 равно:
что указывает на жесткие требования, предъявляемые к активному элементу.
4.3.2. Устойчивость линейных систем с обратной связью
Обратная связь, используемая в
усилителях, может стать причиной
возникновения незатухающих колебаний,
т.е. самовозбуждения. Это может происходить
в силу того, что
- комплексные величины и для некоторых
частот отрицательная обратная связь
может стать положительной. Поэтому
одной из характеристик линейных активных
систем с обратной связью является
устойчивость этих систем к внешним и
внутренним возмущениям. В дальнейшем
цепи, содержащие усилительный элемент,
например, полевой транзистор, будем
называть активными.
Под устойчивостью цепи с обратной связью понимается его способность, будучи выведенным из состояния покоя внешними или внутренними возмущениями, возвращаться в исходное состояние после прекращения действия этих возмущений.
Для активной линейной цепи, которая описывается однородным дифференциальным уравнением
, (4.3.13)
Передаточная функция в операторном виде имеет вид
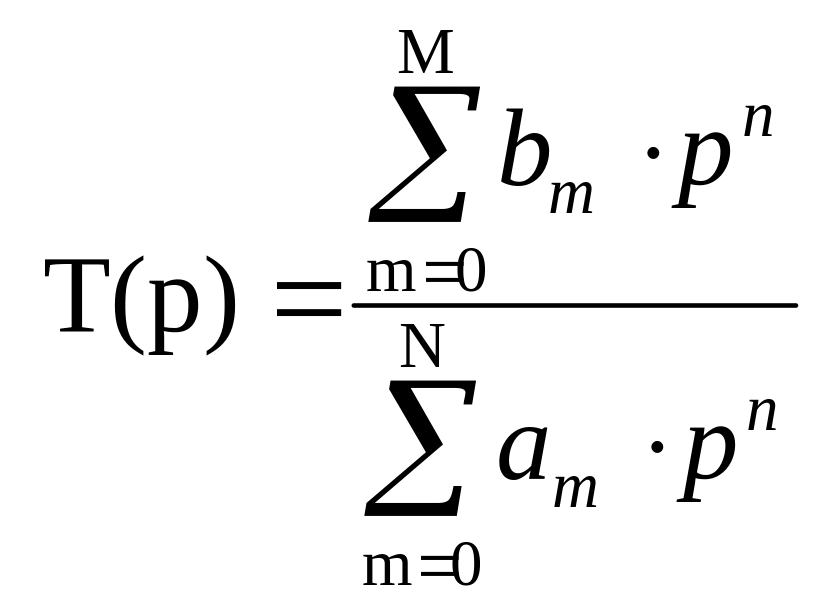. (4.3.14)
Тогда анализ устойчивости сводится к исследованию характеристического уравнения
. (4.3.15)
Необходимым и достаточным условием устойчивости цепи, описываемой уравнением (4.3.13), является отрицательность вещественных частей корней уравнения
, (4.3.16)
соответствующих полюсам передаточной функции цепи обратной связи.
Поэтому переформулируем условие устойчивости.
Необходимым и достаточным условием устойчивости активных линейных систем с обратной связью является расположение полюсов передаточной функции системы в левой полуплоскости комплексного переменного р.
Определение корней уравнения (4.3.16) высоких степеней довольно трудоемкая задача. Поэтому для анализа устойчивости активной цепи с отрицательной обратной связью используются различные критерии в зависимости от поставленной задачи.
Для анализа устойчивости системы при номинальных значениях его элементов используются критерии:
- Рауса-Гурвица (устойчивость цепи определяется по коэффициентам характеристического уравнения);
- Найквиста (устойчивость цепи определяется комплексной частотной характеристикой цепи с обратной связью).
Критерий устойчивости Рауса – Гурвица.
Анализ цепи основан на исследовании главного определителя Рауса -Гурвица
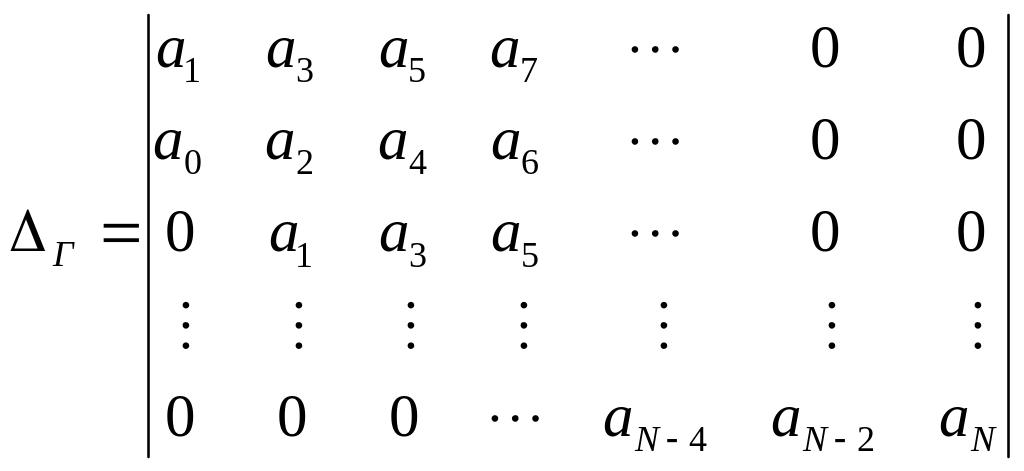, (4.3.16)
который составляется следующим образом:
- в главную диагональ определителя
сверху вниз вписываются все коэффициенты
,
начиная с
в порядке возрастания индекса;
- в первую строку вписываются нечетные коэффициенты ;
- во вторую строку вписываются нечетные
коэффициенты
,
начиная с
;
- третья и четвертая строки заполняются так же, как первая и вторая строка соответственно, но со смещением на один элемент вправо;
- далее строки заполняются аналогично, каждые две строки со смещением вправо на один элемент;
- незаполненные элементы определителя заменяются нулями.
Критерий устойчивости Рауса-Гурвица формулируется следующим образом:
Линейная активная цепь с обратной
связью устойчива, если при
главный
определитель Рауса-Гурвица и все его
миноры
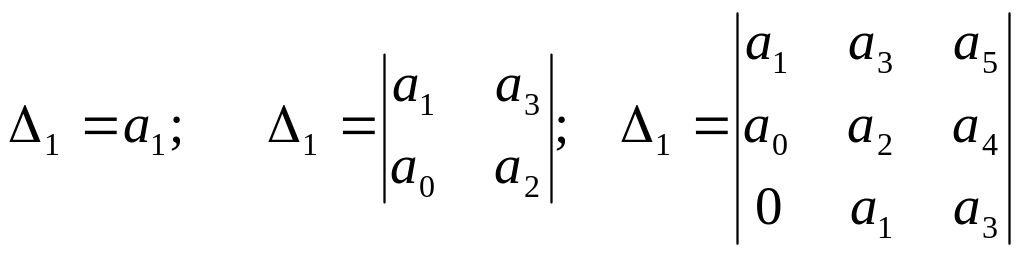и т.д. (4.3.17)
принимают положительные значения.
Критерий устойчивости Найквиста.
Обозначим
. (4.3.18)
Построим
так, чтобы по оси абсцисс откладывалась
величина
,
а по оси ординат – величина
(рис.4.3.2). Длина радиуса – вектора R
на заданной частоте ω
определяет модуль
,
а угол между этим радиусом – вектором
и положительным направлением оси абсцисс
определяет аргумент
.
Такая кривая называется амплитудно -
фазовой характеристикой или годографом
усилителя с цепью обратной связи.
А теперь сформулируем критерий Найквиста.
Активная линейная цепь с обратной связью будет устойчивой, если амплитудно-фазовая характерис-тика (годограф) последовательного соединения усилителя и цепи обратной связи (цепь обратной связи разомкнута) охватывает точку с координатами 1, 0, т.е. точка с координатами 1,0 лежит внутри годографа.
Для определения запаса устойчивости линейной цепи с обратной связью воспользуемся методом D-разбиений.
При этом передаточную функцию линейной цепи представим в следующем виде
. (4.3.19)
Потеря устойчивости электронной цепи будет иметь место при обращении знаменателя уравнения (4.3.19) в нуль. При этом
. (4.3.20)
Указанный выше метод состоит в разбиении плоскости изменяющегося от частоты параметра α на ряд областей D(n,N-n). Эти области соответствуют определенным количествам полюсов передаточной функции в левой (n) и в правой (N-n) полуплоскостях комплексного переменного p. Пример построения областей для линейной цепи с передаточной характеристикой второго порядка представлен на рис.4.3.3.
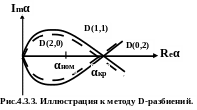
Очевидно, что области устойчивости
D(N,0)
соответствует расположение всех полюсов
в левой полуплоскости (областьD(2,0)
на рис.4.3.3).Степень приближения номинального
значения элемента αном
к критическому значению αкр,
соответствующему уходу из области
устойчивости D(N,0)
количественно отражает запас устойчивости.
В случае вещественности α,
αкр
всегда лежит на пересечении оси Reα
с границей области D(N,0).
Это позволяет ввести меру запаса
устойчивости
:
. (4.3.21)
Пример
Линейная цепь, описываемая комплексной частотно характеристикой
,
устойчива при коэффициенте усиления К=2,9.
Определить будет ли она устойчива при К=4 и каков запас устойчивости по коэффициенту усиления.
1. Приведем комплексную частотную характеристику к виду
2. Составим уравнение
Строим границу D-областей, изменяя частоту в последнем уравнении (рис.4.3.4).
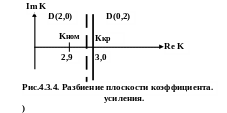
4. При номинальном значении коэффициента усиления Kном, линейная
цепь устойчива и область, включающая в себя это значение, является областью устойчивости D(2,0). Значение К=4 лежит в области D(0,2), что соответствует потере устойчивости, т.к. Kкр=3.
5. Запас устойчивости равен
,
Что указывает на близость цепи к потере устойчивости.