4. Відносна величина структури

Характеризує питому вагу (частку) окремої частини цілого у загальній величині цілого

Відносна величина структури має економічний зміст лише у відсотках. Причому, сума часток завжди = 100%.

В тому випадку, коли сума часток ≠ 100% внаслідок округлень, необхідно здійснити корегування: у найбільшому показнику питомої ваги «зняти» зайвий відсоток, або добавити той, що не дістає.

Приклад: на початок року капітал підприємства становив 214 млн грн. З нього власний капітал = 146 млн грн, Залучений = 68 млн грн. Визначити структуру капіталу підприємства.

Висновок: сума власного капіталу складає 68,2% загальної суми капіталу підприємства, а сума залученого капіталу 31,8%.

5. Відносна величина координації

Характеризує співвідношення однієї частини цілого до іншої частини цього ж цілого. Показує, у скільки разів або на скільки відсотків одна частина більша іншої чи на скільки відсотків одна частина менше іншої або скільки відсотків від неї складає.

Приклад: визначити відносні величин координації між власним та залученим капіталом підприємства.

Висновок: сума власного капіталу перевищує суму залученого капіталу підприємства у 2,147 раза (більше, ніж у 2 рази) або на 114,7%.

Висновок: сума залученого капіталу менше, ніж сума власного капіталу підприємства на 53,4% або сума залученого капіталу складає 46,6% від суми власного капіталу.

На кожну гривню власного капіталу підприємства припадає в середньому 46,6 копійок залученого капіталу.

6. Відносна величина порівняння

Характеризує співвідношення однойменних показників, взятих за один і той самий період часу (або на один і той самий момент часу), але стосовно різних територій або об’єктів. За своєю економічною інтерпретацією, відносна величина порівняння співпадає з відносною величиною координації;

7. Відносна величина інтенсивності – характеризує ступінь розповсюдження явища у певному середовищі: її отримують у тому випадку, коли знаходиться співвідношення різнойменних показників. В кожному конкретному випадку відносна величина інтенсивності має свою особливу формулу розрахунку, а також одиниці вимірювання.

Але всі відносні величини інтенсивності характеризують одне і те саме: скільки одиниць показника, що знаходиться в чисельнику припадає в середньому на одну одиницю показника, що знаходиться в знаменнику. Прикладами відносних величин інтенсивності можуть бути такі показники:

Середні величини, способи їх розрахунку

Середня величина – узагальнюючий показник, який характеризує типовий розмір ознаки у розрахунку на одиницю однорідної сукупності в конкретних умовах місця та часу.

У статистиці найбільш поширеними э два види середніх величин:

1. Середня арифметична;

2. Середня гармонічна.

Кожен із цих двох видів середніх величин може мати 2 форми:

1. Середня проста;

2. Середня зважена.

В результаті отримуємо 4 формули розрахунку середніх величин:

1. Середня арифметична проста:

, де х – значення середньої ознаки у кожної одиниці сукупності,

n – кількість одиниць сукупності;

2. Середня арифметична зважена:

, де х – значення середньої ознаки в кожній групі,

m(t) – кількість одиниць сукупності в кожній групі.;

3. Середня гармонічна проста

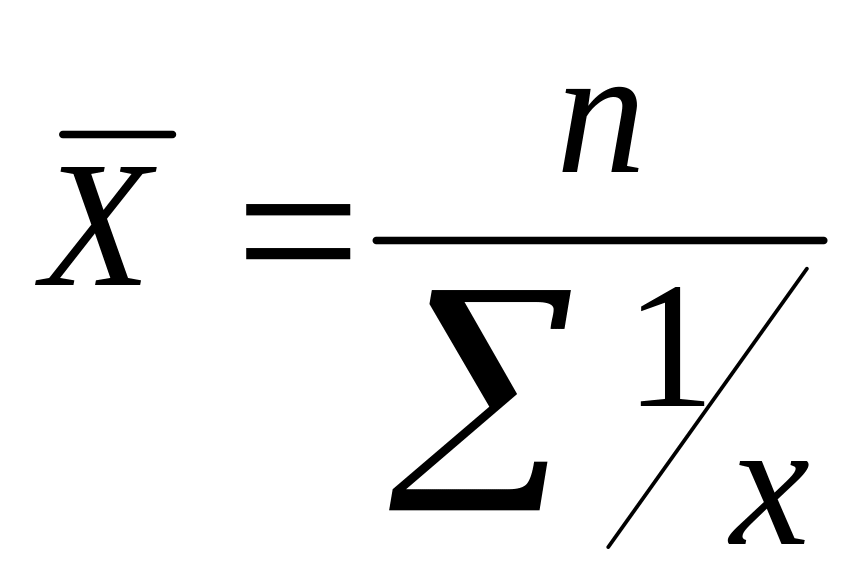, де х – значення середньої ознаки у кожної одиниці сукупності,

m – кількість одиниць сукупності;

4. Середня гармонічна зважена

, де х – значення середньої ознаки у кожної групі,

M – узагальнюючий (сумарний) показник.

У статистиці (на відміну від математики) в кожному конкретному випадку для розрахунку обирають одну єдиноможливу формулу розрахунку середньої величини. Вибір формули розрахунку здійснюється на основі так званої «логічної» формули, а також залежно від наявності вихідних даних.

«Логічна» формула – словесне описання способу розрахунку осереднюваної ознаки.

Вибір виду середньої величини здійснюється так:

1. Якщо відомий знаменник логічної формули і невідомий чисельник, то обирають середню арифметичну;

2. Якщо відомий чисельник логічної формули, а невідомий – знаменник, то обирають середню гармонічну.

Вибір форми середньої величини:

1. Якщо вихідна інформація є не згрупованою, то обирають середню просту;

2. Якщо вхідна інформація є згрупованою і ваги варіантів нерівні, то обирають середню зважену.

Алгоритм розрахунку середньої величини:

1. Записується логічна формула;

2. Обирається формула розрахунку середньої величини;

3. Здійснюється розрахунок середньої;

4. Робиться висновок.

Приклад:

Є такі дані по двох фермерських господарствах:

Вид культур	Фермерське гос-во №1		Фермерське гос-во №2
	Посівна площа, га m	Врожайність з 1 га, ц x	Валовий збір, ц M	Врожайність с 1 га, ц X
Пшениця	1540	20	32240	21
жито	120	19	1620	18

Визначити:

В якому господарстві середня врожайність зернових культур вища і на скільки %?

Фермерське господарство №1:

Оскільки відомий знаменник логічної формули, а невідомий – чисельник, то вид середньої – арифметична.

Оскільки вихідна інформація є згрупованою, причому ваги варіантів нерівні, то формою середньої буде зважена.

Таким чином, в даному випадку для розрахунку середньої величини потрібно обрати формулу середньої арифметичної зваженої:

У фермерському господарстві №1 з одного гектару посівів збирають в середньому 19,9 ц зернових культур.

Фермерське господарство №2:

Оскільки відомий чисельник логічної формули і невідомий знаменник, причому вхідна інформація згрупована і ваги нерівні, то для розрахунку потрібно обрати формулу середньої гармонічної зваженої:

Висновок: у фермерському господарстві №2 з 1 га посівів збирають в середньому 20,8 ц зернових культур.

Знайдемо відносну величину порівняння:

Висновок: у фермерському господарстві №2 середня врожайність зернових культур вища на 4,5%.