Вопросы и упражнения
1. В
каком случае векторное произведение
двух векторов равно
?
а)
оба вектора нулевые; б)
хотя бы один из них равен
;
в) векторы перпендикулярны; г)
векторы коллинеарны.
2. При
каком значении
 векторы
векторы
 ,
,
 являются коллинеарными?
являются коллинеарными?
Ответ:
 .
.
3. Доказать,
что векторное произведение не изменится,
если к одному из сомножителей добавить
вектор, коллинеарный другому сомножителю.
4. Вычислить
векторное произведение векторов,
заданных своими декартовыми координатами
 ,
,
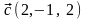 .
.
Ответ:
 .
.
5. При
каком условии справедливо равенство
 ,
если
?
,
если
?
Ответ:
 коллинеарен вектору
.
коллинеарен вектору
.
6. Дать
алгебраическое доказательство того,
что смешанное произведение трех
компланарных векторов равно нулю.
Указание:
воспользоваться следствием к теореме
3.4.2.
7.
Вычислить объем параллелепипеда,
построенного на векторах
 ,
,
 ,
,
 .
Какую ориентацию имеет тройка
,
,
?
.
Какую ориентацию имеет тройка
,
,
?
Ответ:
25, отрицательная ориентация (левая
тройка).
8.
Проверить справедливость равенства
 .
.
9.
Доказать компланарность векторов
,
,
,
если
 .
.
10. Доказать,
что если
,
,
то
 .
.
12


 векторы
векторы
 ,
,
 являются коллинеарными?
являются коллинеарными? .
. ,
,
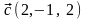 .
. .
. ,
если
?
,
если
? коллинеарен вектору
.
коллинеарен вектору
. ,
,
 ,
,
 .
Какую ориентацию имеет тройка
,
,
?
.
Какую ориентацию имеет тройка
,
,
? .
. .
. .
.