
3.19. Смешанное произведение трех векторов
Определение
3.19.1. Смешанным
произведением
трех векторов
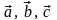 называется число
называется число
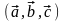 =
= 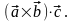 (3.19.1)
(3.19.1)
Из
определения ясно, что если хотя бы один
из данных векторов нулевой, то смешанное
произведение, очевидно, равно нулю.
Больше того, когда два из них коллинеарны,
например,
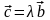 ,
то по определению векторного произведения
,
то по определению векторного произведения
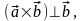 следовательно,
следовательно,
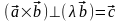 ,
отсюда
,
отсюда

Теорема 3.19.1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения, т. е. = 0.
Доказательство.
Необходимость.
Если векторы
компланарны, то вектор
перпендикулярен плоскости векторов
и
,
а, следовательно, он перпендикулярен
вектору
,
поэтому
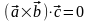 .
.
Достаточность. Пусть = 0. Будем считать, что среди данных векторов нет нулевого, а также никакие два из них не являются коллинеарными, ибо иначе сразу можно утверждать, что векторы компланарны.
Тогда
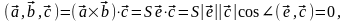
откуда
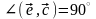 ,
следовательно, вектор
лежит в плоскости векторов
,
,
т. е. векторы
компланарны.
,
следовательно, вектор
лежит в плоскости векторов
,
,
т. е. векторы
компланарны.
Теорема 3.19.2.
Смешанное произведение трех векторов

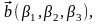
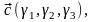 заданных своими аффинными координатами,
вычисляется по формуле
заданных своими аффинными координатами,
вычисляется по формуле
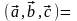
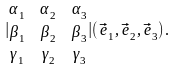 (3.19.2)
(3.19.2)
Доказательство. Формула (3.19.2) следует из формулы (3.18.1) и (3.16.3).
Следствие
3.19.1. Смешанное
произведение трех векторов

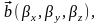
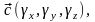 заданных своими декартовыми координатами,
находится по формуле
заданных своими декартовыми координатами,
находится по формуле
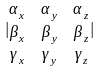 =
=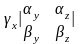 –
–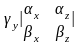 +
+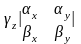

Теорема 3.19.3. Смешанное произведение трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах-сомножителях после приведения их в общее начало, взятому со знаком “+”, если тройка правая, и со знаком “–”, если эта тройка левая.
Доказательство. Пусть S — площадь параллелограмма, построенного на векторах и после приведения их в общее начало. Допустим, что — орт вектора , а h — высота параллелепипеда, построенного на векторах , при условии, что основанием служит параллелограмм, построенный на векторах и (рис. 3.19.1, 3.19.2).
Рис. 3.19.1 |
Рис. 3.19.2 |
Ясно,
что
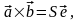
 .
Отметим, что
.
Отметим, что
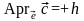 ,
если тройка векторов
является правой, и
,
если тройка векторов
является правой, и
 ,
если — левой.
,
если — левой.
Тогда
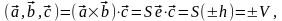
где V объем параллелепипеда, причем берем “+”, если тройка правая, и “–”, если эта тройка — левая.
Следствие 3.19.2. Верно равенство
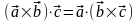 . (3.19.3)
. (3.19.3)
Доказательство.
В самом деле, в силу коммутативности
скалярного произведения
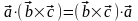 ,
поэтому достаточно показать, что
,
поэтому достаточно показать, что
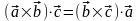 .
Последнее равенство очевидно, ибо
абсолютная величина каждого из чисел
равна объему параллелепипеда, построенного
на векторах
,
исходящих из общей точки, и, кроме того,
эти числа имеют одинаковые знаки, так
как тройки векторов
и
.
Последнее равенство очевидно, ибо
абсолютная величина каждого из чисел
равна объему параллелепипеда, построенного
на векторах
,
исходящих из общей точки, и, кроме того,
эти числа имеют одинаковые знаки, так
как тройки векторов
и
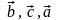 имеют одинаковую ориентацию.
имеют одинаковую ориентацию.
Из теоремы 3.19.3 следует, что ( ) > 0 (( ) <0), когда тройка векторов — правая (левая). Поэтому правую (левую) тройку векторов иногда называют положительно (отрицательно) ориентированной.
3.20. Двойное векторное произведение
Определение
3.20.1. Двойным
векторным произведением трех
векторов
называется вектор
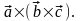
Теорема 3.20.1. Двойное векторное произведение равно среднему вектору произведения, умноженному на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных, т. е.
 (3.20.1)
(3.20.1)
Доказательство.
Пусть
 ,
где
— орт векторного произведения,
,
где
— орт векторного произведения,
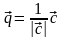 — орт вектора
.
— орт вектора
.
Введем
вспомогательный орт
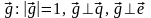 ,
причем тройка векторов
,
причем тройка векторов
 — правая, а также углы
— правая, а также углы
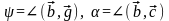 (рис. 3.20.1). Площадь параллелограмма,
построенного на векторах
и
,
равна
(рис. 3.20.1). Площадь параллелограмма,
построенного на векторах
и
,
равна
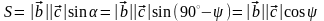 . (3.20.2)
. (3.20.2)

Рис. 3.20.1
Пусть
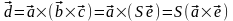 .
По определению векторного произведения
вектор
.
По определению векторного произведения
вектор
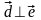 ,
поэтому
лежит в плоскости векторов
и
,
отсюда
,
поэтому
лежит в плоскости векторов
и
,
отсюда
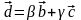 .
С другой стороны
.
С другой стороны
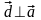 ,
т. е.
,
т. е.
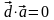 .
Используя выражение для вектора
,
имеем
.
Используя выражение для вектора
,
имеем
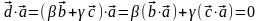 ,
,
отсюда
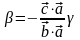
и, окончательно,
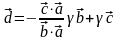 . (3.20.3)
. (3.20.3)
Тройка векторов образует ортонормированный базис, в котором вектор представим в виде:
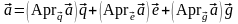 . (3.20.4)
. (3.20.4)
Вектор
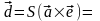
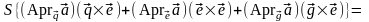
 (3.20.5)
(3.20.5)
Сравнивая полученное выражение для вектора с соотношением (3.20.3), имеем тождество
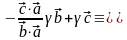
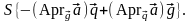
Умножим
обе части этого тождества скалярно на
вектор
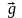 .
Тогда с учетом соотношений
.
Тогда с учетом соотношений
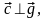
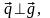
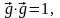
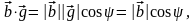
 и формулы (3.20.2) имеем
и формулы (3.20.2) имеем
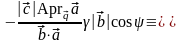
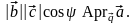
После
всех сокращений получаем
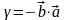 ,
следовательно,
,
следовательно,
 ,
а тогда из формулы (3.20.3) имеем (3.20.1).
,
а тогда из формулы (3.20.3) имеем (3.20.1).
Следствие 3.20.1.
Справедлива
формула
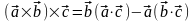 .
.
Доказательство.
С учетом свойств векторного произведения
и формулы (3.20.1) имеем
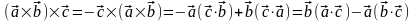 .
.
Следствие 3.20.2. Для любых векторов справедлива формула Лагранжа
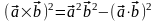 .
.
Доказательство.
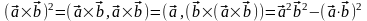 .
.


